Navch._posibnuk_Ivaschyk

rτ (0,1)– додатна. Якщо rτ лежить в як завгодно малому околі точки

нуль, то кореляція між результативним фактором та факторомаргументом, значення якого є зсунутими на лаг часу τ , відсутня. Найбільше абсолютне значення цього показника визначає значення часового лага. Звичайно, лаг часу існує, якщо абсолютне значення коефіцієнта взаємної кореляції є близьким до одиниці. Зауважимо, що за умови існування декількох близьких до одиниці абсолютних значень коефіцієнта взаємної кореляції маємо декілька часових лагів для двох часових рядів. Якщо τ = 0, то коефіцієнт взаємної кореляційної функції перетворюється у коефіцієнт парної кореляції. Графік залежності коефіцієнта взаємної кореляції від періоду часу τ називають корелограмою функції.

Приклад 17.3. Розрахувати значення коефіцієнтів взаємної кореляції та побудувати графік кореляційної функції для наступних статистичних даних залежності витрат на харчування (уt, грош. од.) від рівня доходів (xt, грош. од.) при максимальному значенні лага часу, рівному восьми місячним періодам.

561

♦Розв’язування.

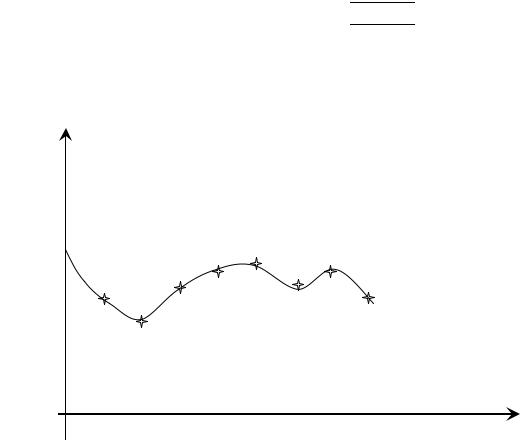
Побудуємо графік кореляційної функції (рис. 17.3.1).

r(τ)

1

0,8

0,6

0,4

0,2

Рис. 17.3.1

Аналізуючи значення коефіцієнтів взаємної кореляційної функції, робимо висновок, що рівень доходів значно впливає на рівень витрат на харчування протягом всіх восьми періодів часу. При цьому коефіцієнт парної кореляції для показників є найбільшим (τ=0), що свідчить про найбільшу схильність людей витрачати кошти на харчування у найближчому поточному періоді.

У загальному економетрична модель розподіленого лага (17.5) описує ситуацію: якщо в деякий момент часу t відбувається зміна незалежної змінної х, то вона буде впливати на значення змінної y протягом τ наступних моментів часу.

Коефіцієнт регресії b0 при змінній xt характеризує середню абсолютну зміну yt при зміні xt на одиницю свого вимірювання в деякий фіксований момент часу t без урахування впливу лагових значень фактора x. Цей коефіцієнт називають короткотерміновим мультиплікатором.

562

На момент часу t+1 сукупна дія факторної змінної xt на результат yt складе (b0+b1) умовних одиниць, на момент t+2 цю дію можна охарактеризувати сумою (b0+b1+b2) і т.д. Одержані таким чином суми мають назву проміжних мультиплікаторів.

З урахуванням кінцевої величини лага можна сказати, що зміна змінної xt в момент часу t на 1 у. о. призведе до загальної зміни результату через τ моментів часу на (b0+b1+…+bτ ) абсолютних

де b – довготерміновий мультиплікатор, який показує величину абсолютної зміни в довготерміновому періоді t+τ-го результату y під

Назвемо отримані величини відносними коефіцієнтами моделі з розподіленим лагом. Якщо всі коефіцієнти bj мають однакові знаки, то для будь-якого j маємо:

βj > 0, j = 0,τ,

τ

∑βj =1.

j=0

Вцьому випадку відносні коефіцієнти βj будуть вагою для

відповідних коефіцієнтів bj. Кожен із них вимірює частку загальної зміни результативної ознаки в момент часу t+j.

Знаючи значення βj, за допомогою стандартних формул можна визначити ще дві важливі характеристики моделі множинної регресії, а саме: величину середнього та медіанного лага. Середній лаг розраховується за формулою зваженого середньоарифметичного:

j=0

де l – середній період, протягом якого буде здійснюватися зміна результату під дією зміни фактора в момент часу t. Незначна величина середнього лага свідчить про відносно швидке реагування результату на зміну фактора, тоді як його високе значення говорить про те, що дія фактора на результат відбувається протягом довгого періоду часу.

563

lMe

Медіанний лаг – величина лага, для якого ∑β j ≈ 0,5, тобто це

j=0

той період часу, за який з моменту t буде реалізована половина загальної дії фактора на результат.

Розглянемо умовний приклад.

Приклад 17.4. За результатами вивчення залежності обсягів ВВП від обсягу інвестицій отримана така модель з розподіленим лагом:

yt = 2.6 + 0,2xt + 0,8xt −1 +1,1xt −2 +1,5xt −3 +1,8xt −4 + 2,6xt −5 .

♦Розв’язування.

Короткотерміновий мультиплікатор моделі рівний 0,2. Це значить, що збільшення обсягу інвестицій на 1 млн. грн. призводить до зростання середнього обсягу ВВП на 0,2 млн. грн. в тому ж періоді. Під впливом збільшення інвестицій обсяг ВВП зросте в момент часу: t+1 на 0,2+0,8=1,0 (млн. грн.); t+2 на 1,0+1,1=2,1 (млн. грн.); t+3 на 2,1+1,5=3,6 (млн. грн.); t+4 на 3,6+1,8=5,4 (млн. грн.); t=5 на 5,4+2,6=8,0 (млн. грн.). Довгостроковий мультиплікатор зазначеної моделі становитиме b = 0,2 + 0,8 +1,1+1,5 +1,8 + 2,6 = 8,0. У довготерміновій перспективі (наприклад, через 5 місяців) збільшення обсягу інвестицій на 1 млн. грн. у теперішній момент часу призведе до загального росту обсягу ВВП на 8,0 млн. грн.

Відносні коефіцієнти регресії окресленої моделі такі:

Отже, 2,5 % загального збільшення обсягу ВВП, який зумовлений збільшенням обсягу інвестицій, відбувається в поточному моменті часу; 10,0 % – в момент t+1; 12,5 % – в момент t+2; 18,8 % – в момент t+3; 22,5 % – в момент t+4; 29,5 % – в момент t+5.

Середній лаг в моделі визначаємо таким чином:

l = 0 0,025 +1 0,100 + 2 0,125 +3 0,188 + 4 0,225 +5 0,295 = 3,289 р.

Знайдена величина лагу говорить про те, що більша частина ефекту впливу збільшення інвестицій проявляється в середньому через 3,289 роки.

Оскільки β0 + β1 + β2 + β3 = 0,025 + 0,100 + 0,125 + 0,188 = 0,438, а

β0 + β1 + β2 + β3 + β4 = 0,438 + 0,225 = 0,663, то можна стверджувати,

564

що медіанний лаг становить приблизно 3,5 років, тобто половина впливу збільшення інвестицій на збільшення обсягу ВВП реалізується за 3,5 роки. ♦

Викладені вище методи аналізу параметрів моделі з розподіленим лагом дійсні тільки в припущенні, що всі коефіцієнти при поточних і лагових значеннях досліджуваного фактора мають однакові знаки. Це припущення цілком виправдане з економічної точки зору: вплив одного й того ж фактора на результат повинен бути однонаправленим незалежно від того, з яким числовим лагом вимірюється сила чи тіснота зв’язку між цими ознаками. Однак на практиці отримати статистично значущу модель, параметри якої мали б однакові знаки, особливо при більшій величині лага є надзвичайно складно.

Застосування звичайного МНК до таких моделей у більшості випадків є трудомісткою справою через такі причини:

•поточні та лагові значення незалежної змінної, як правило, тісно пов’язані одні з другими. Через це оцінка параметрів моделі здійснюється в умовах високої мультиколінеарності факторів;

•при великій величині лага знижується число спостережень, на основі яких будується модель і збільшується число її факторних ознак, що призводить до втрати числа ступенів свободи в моделі;

•в моделях із розподіленим лагом часто виникає проблема автокореляції залишків.

Вищевказані обставини призводять до значної невизначеності

відносно оцінок параметрів моделі, зниження їхньої точності та отримання неефективних оцінок.

Чистий вплив факторів на результат в таких умовах виявити неможливо. Через це на практиці параметри моделі з розподіленим лагом враховують певні обмеження на коефіцієнти регресії та умови вибраної структури лага.

17.4.Оцінювання та побудова економетричних моделей динаміки

Поточні та лагові значення факторної змінної мають різну силу впливу на результативну змінну моделі. Кількісно сила зв’язку між результатом і значеннями факторної змінної, яка відноситься до різних моментів часу, вимірюється з допомогою коефіцієнтів регресії при факторних змінних. Якщо побудувати графік залежності цих коефіцієнтів від величини лага, то можна отримати графічне

565

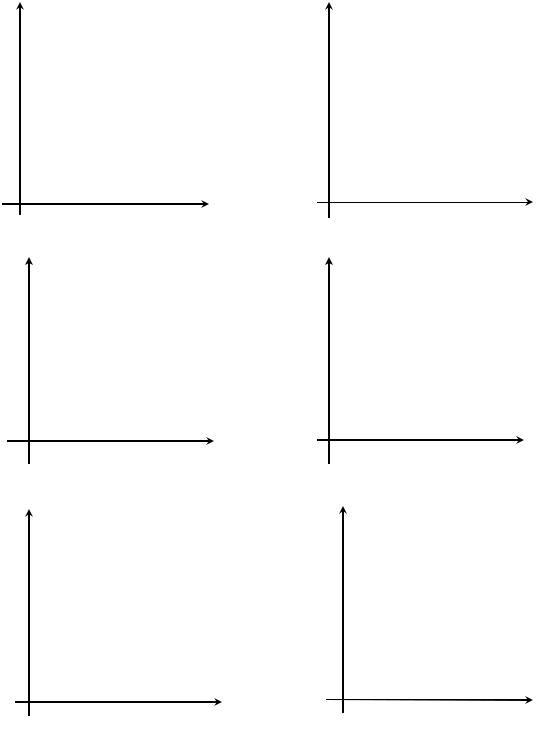
представлення структури лага, інакше, розподіл у часі дії факторної змінної на результат. Враховуючи те, що структура лага може бути різною, графічно представимо основні форми лага (рис.17.4.1).

Рис. 17.4.1. Основні форми лага: а) лінійна; б) геометрична; в) перевернута V-парабола; г) -е) поліноміальна

Якщо з ростом величини лага коефіцієнти при лагових змінних спадають у часі, то має місце лінійна (17.4.1а) або геометрична

566

структура лага (17.4.1б). Якщо лагові впливи фактора на результат не мають тенденції до спаду в часі, то має місце один із варіантів, представлених на рис. 17.4.1 в)-е). Структуру лага (17.4.1в) називають «перевернутою» V-подібною структурою. Основна її властивість – симетричність лагових впливів відносно деякого середнього лага, який характеризується найбільш сильним впливом фактора на результат. Графіки, представлені на рис. 17.4.1 г) і е) свідчать про поліноміальну структуру лага.

Графічний аналіз структури лага аналітичним способом можна провести з допомогою відносних коефіцієнтів βj регресії. Основна трудність у виявленні структури лага полягає в тому, як отримати значення параметрів bj (або βj). Попередньо було відзначено, що звичайний МНК рідко буває корисним у таких випадках. Через це в більшості випадків припущення про структуру лага базуються на загальних положеннях економічної теорії, на дослідженні взаємозв’язку показників або на результатах проведення емпіричних досліджень, або на іншій апріорній інформації.

17.4.1. Модель Койка

Одним із методів вирішення проблеми оцінки коефіцієнтів лагових моделей є припущення, що вплив пояснювальних змінних на результативний показник є нескінченним у часі, тобто величина лага є нескінченною. Таким чином, для опису функціонування економічних формувань як на макро-, так і на мікрорівні необхідно використовувати економетричну модель із нескінченним лагом:

Оскільки ця модель містить нескінченне число факторних змінних, то її параметри неможливо обчислити, використовуючи МНК. Вчений Я.М. Койк запропонував припущення, що вплив лагових значень пояснювальної змінної на результативний фактор зменшується у геометричній прогресії відповідно до збільшення величини лага часу. На рис. 17.4.1 геометричній структурі лага відповідає варіант б).

Я.М. Койк припустив, що:

Рівняння (17.11) називають моделлю Койка. Таким чином, результативний показник змінюється під впливом фактора-аргументу у початковий період на b0 , через період t=1–b1 = b0λ , через період

567

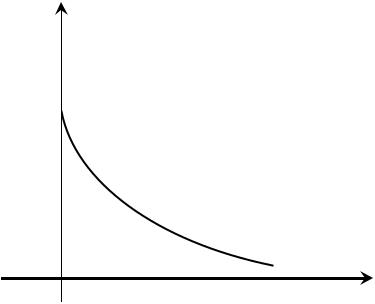
поліноміальний темп зменшення впливу в часі лагових значень пояснювального фактора на кінцевий результат. Розглянемо графічну інтерпретацію параметрів моделі Койка (рис. 17.4.1.1).

bj

b0

bj = b0λj

Час (j)

Рис. 17.4.1.1. Графічне представлення параметрів моделі Койка

Далі розглянемо алгоритм «перетворення Койка», який дає можливість перейти від моделі з нескінченними розподіленими лагами до моделі авторегресії, що містить дві незалежні змінні xt i yt-1. За допомогою (17.11) виразимо коефіцієнти bj моделі (17.10) через b0 і λ:

Для періоду t–1 модель (17.12) матиме вигляд:

Здійснивши перетворення в (17.15), ми отримуємо модель

568

Зазначена модель є авторегресійною моделлю, тому що лагова величина залежної змінної (yt −1) з’являється у правій частині

рівняння. Визначивши її параметри, ми знайдемо значення λ та оцінки параметрів а і b0 вихідної моделі. За допомогою (17.11) визначають параметри b1, b2,… моделі (17.10). Застосувавши звичайний МНК до оцінки параметрів моделі (17.16), отримаємо зміщені оцінки параметрів через присутність в моделі фактора лагової результативної змінної yt-1.

Зауважимо, що обмеження на значення λ>0 забезпечує однакові знаки всіх коефіцієнтів bj>0, а при λ<0 знаки коефіцієнтів bj поперемінно змінюються. Чим ближче значення λ до 0, тим вищий темп зниження впливу фактора на результат у часі, тим більша частка впливу на результат припадає на поточне значення фактора xt.

Незважаючи на нескінченне число лагових змінних в моделі (17.10), геометрична структура лага дає можливість визначити величину середнього та медіанного лага в моделі Койка.

Нижченаведене рівняння визначає довготерміновий вплив лагових значень факторної ознаки на кінцевий результат функціонування економічної системи:

оскільки сума коефіцієнтів авторегресійної моделі (17.10) – це сума геометричної прогресії.

Середній лаг визначається таким чином:

Легко зауважити, що для λ=0,5 середній лаг дорівнює одиниці (l =1), а для λ<0,5–l <1, тобто тривалість впливу фактора на результат у середньому є меншою від одного періоду часу. Величину (1–λ) зазвичай інтерпретують як швидкість, з якою протікає адаптація результату в часі відповідно до зміни факторної ознаки. Для виконання розрахунку медіанного лага необхідне виконання такої умови:

569

Приклад 17.5. У таблиці наведені дані про обсяги доходів ( xt ) та споживання ( yt ). Розрахуємо параметри авторегресійної моделі Койка.

♦Розв’язування.

a (1−λ)=1,4618; b0 = 0,669772; λ = 0,279226; a =1,387397; b0 = 0,669772.

Отже, маємо параметри моделі:

b1 = 0,187018; b2 = 0,05222 і т. д.

Підставляючи значення b0 і λ у рівняння (17.17), одержуємо

коефіцієнт довготермінового впливу лагових значень пояснювальної змінної обсягу доходів на результативний показник – обсяг споживання, рівний:

570