Задача 3.2 (33.2)

Точка привеса математического маятника длиной движется по вертикали равноускоренно. Определить период Т малых колебаний маятника в двух случаях: 1) когда ускорение точки привеса направлено вверх и имеет какую угодно величину; 2) когда это ускорение направлено вниз и величина его.

Решение

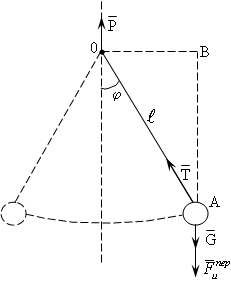
Рис. 3.2

На рис. 3.2 показан схематично математический маятник, точка подвеса которого «О» движется ускоренно вверх с ускорением . Рассмотрим положения маятника в некотором произвольном положении при отклонении нити маятника на угол.

Движение груза маятника вокруг точки подвеса «О» является относительным, а движение подвеса вверх – переносное.

На груз маятника действуют силы: – сила тяжести груза маятника,– сила натяжения нити маятника,– сила инерции, действующая на груз маятника вследствие ускоренного движения точки подвеса. Так как ускорение точки подвеса направлено вверх, то сила инерции будет направлена в противоположную сторону относительно направления ускорения точки подвеса.

Применим дифференциальное уравнение для вращательного движения твердого тела для груза маятника:

, (1)

где – момент инерции маятника относительно оси, проходящий через точку подвеса и перпендикулярно плоскости чертежа:

, – масса груза маятника.

–сумма моментов сил относительно оси .

, (2)

где – момент инерции силы тяжести относительно оси;

–момент инерции силы натяжения нити относительно оси ;

–момент инерции силы инерции вследствие ускоренного движения точки подвеса относительно оси .

Значение момента будет равно:

. (3)

Момент силы натяжения нити относительно оси равен нулю, так как направление силы проходит через ось:.

Значение момента будет равно:

. (4)

Подставляя выражения (3) и (4) в формулу (2), получим:

.

После преобразования этого выражения, получим:

. (5)

Подставляя выражение (5) в формулу (1), получим:

.

Так как , то после преобразования, получим:

, или

.

Учитывая, что колебания малые, то , тогда

.

Это дифференциальное уравнение описывает свободные колебания. Тогда частота собственных колебаний маятника будет:

.

Так как , где– период колебания маятника, то

.

Таким образом, если точка подвеса маятника перемещается вверх с ускорением , то период колебания маятника будет равен:

.

Рассмотрим случай, когда точка подвеса перемещается вниз с ускорением (рис. 3.4).

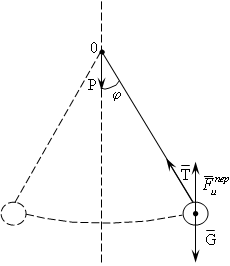
Рис. 3.4

В этом случае на груз маятника действуют силы итак же как и в первом случае, а силанаправлена в сторону, противоположную ускорению(рис. 3.4). Тогда момент силы инерции относительно осибудет:

.

Сумма моментов сил, действующих на груз маятника, будет

,

после преобразований, получим:

. (6)

Подставляя выражение (6) в уравнение (1), получим:

Учитывая, что , после подстановки и преобразований, получим:

.

Так как колебания малые, то , тогда

.

Данное дифференциальное уравнение описывает свободные колебания с собственной частотой, равной

.

Тогда – период колебания маятника при движении точки подвеса вниз с ускорением.

Ответ: 1. ;

2. .