Задача 4.2 (32.93)

Тело весом 2 кГ, прикрепленное пружиной к неподвижной точке А, движется по гладкой наклонной плоскости, образующей угол с горизонтом, под действием возмущающей силыкГ и силы сопротивления, пропорциональной скорости:кГ. (рис. 4.8). Коэффициент жесткости пружиныкГ/см. В начальный момент тело находилось в покое в положении статического равновесия. Найти уравнение движения тела, периодысвободных ивынужденных колебаний, сдвиг фазы вынужденных колебаний и возмущающей силы.

Решение

Рис. 4.8

Обозначим силы, действующие на груз: – сила тяжести груза,– возмущающая сила,– сила упругости пружины,– сила сопротивления. Поместим начало координат в точку статического равновесия и направим ось х по направлению растяжения пружины. Составим дифференциальное уравнение движения груза:

.

Спроектируем это векторное уравнение на ось х:

, (1)

где ;

;

;

.

Подставляя эти выражения в уравнение (1), получим:

.

Учитывая, что – при статическом равновесии.

После преобразований, получим:

, или

.

Подставляя численные значения, получим:

,

. (2)

Решение полученного дифференциального неоднородного уравнения второго порядка ищем в виде:

,

где – общее решение однородного дифференциального уравнения;

–частное решение неоднородного дифференциального уравнения.

Однородное дифференциальное уравнение имеет вид:

.

Для решения этого однородного дифференциального уравнения составим характеристическое уравнение:

.

, так как корни характеристического уравнения комплексные, то решение ищем в виде:

.

Решение ищем в виде:

,

где ;.

Коэффициент определяется из формулы:

; тогда: _,

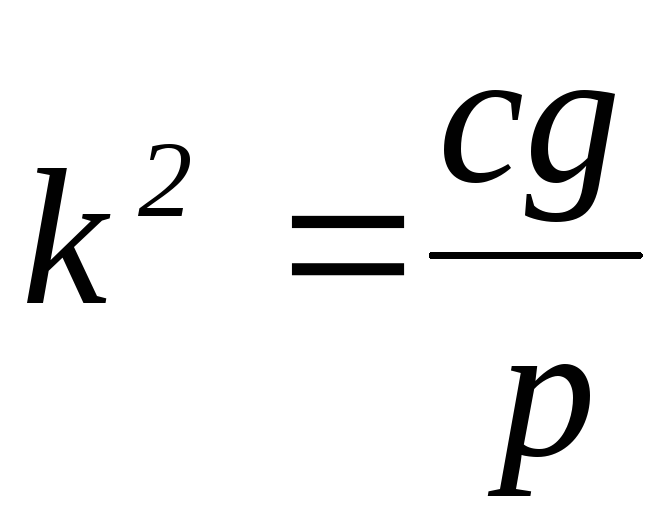подставляя численные значения, получим:

; ;.

Так как , по условию задачи,, тогда

.

; ;.

Отсюда следует, что .

Решение уравнения (1) будет иметь вид:

. (3)

Коэффициенты С₁ и С₂ определим из начальных условий: ,,. Подставим начальные условия в уравнение (3):

; .

Продифференцируем уравнение (3) по времени и подставим начальные условия:

.

Подставив начальные условия, получим:

.

Тогда решение уравнения (2) будет иметь вид:

.

Ответ: .

Вопросы для самоконтроля:

1. Что такое свободные колебания?

2. Что такое затухающие колебания?

3. Что такое апериодическое движение?

Задачи, рекомендуемые для самостоятельного решения: 32.1 – 32.50., 32.51. – 32.74. [3].

Литература: [1] – [5].

Лекция 5

1. Вынужденные колебания точки при отсутствии сопротивления

Пусть на материальную точку М массой m действуют: восстанавливающая сила и периодически изменяющаяся со временем сила, проекция которой на ось ох равна (рис. 5.1):

.

Сила называется возмущающей силой, а колебания, которые происходят под действием такой силы, называются вынужденными. Величина– называется частотой возмущающей силы,– амплитуда возмущающей силы.

Рис. 5.1

Дифференциальное уравнение движения точки М в этом случае имеет вид (в проекциях на ось ох):

, (5.1)

Разделим обе части уравнения на массу:

, (5.2)

Обозначим: , тогда

, (5.3)

Это дифференциальное неоднородное уравнение второго порядка. Решение уравнения (5.1) ищем в виде:

, (5.4)

где – общее решение однородного дифференциального уравнения;

–частное решение неоднородного дифференциального уравнения.

Для однородного дифференциального уравнения:

, (5.5)

Решение находим в виде:

, (5.6)

где С₁ и С₂ – постоянные коэффициенты, определяемые по начальным условиям.

Пусть , тогда решениеищем в виде:

, (5.7)

(решение ищем в форме правой части дифференциального уравнения).

Определяя вторую производную по времени для (5.7) и подставив в уравнение (5.3), получим:

, (5.8)

Приравнивая коэффициенты при , получим:

Подставляя это выражение в уравнение (5.7), получим:

, (5.9)

Подставляя решение в уравнение (5.4), получим:

, (5.10)

Делая замену: , получим

. (5.11)

Из уравнения (5.11) видно, что колебания точки складываются из:

1) колебаний с амплитудой (зависящей от начальных условий) и частотой, называемых собственными колебаниями; 2) колебаний с амплитудой(не зависящей от начальных условий) и частотой, которые называются вынужденными колебаниями, где

, (5.12)

В случае если , т.е. когда частота возмущающей силы равна частоте собственных колебаний, это явление называется резонансом.

– амплитуда возмущающей силы.

Разделим числитель и знаменатель на и получим:

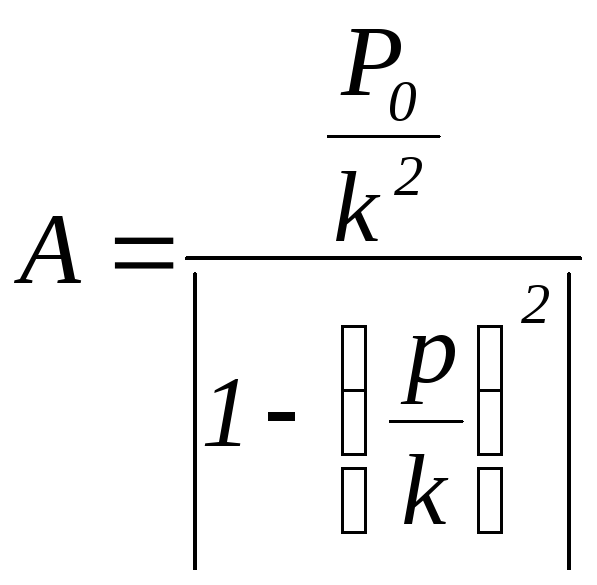, (5.13)

Так как , то, учитывая, что, то:, тогда

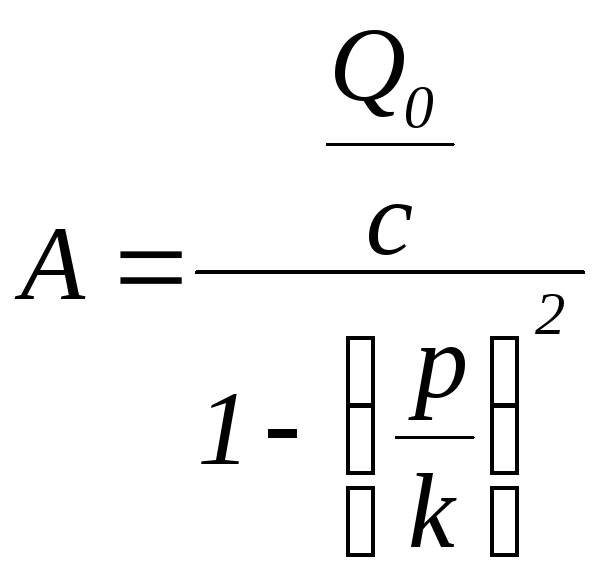, (5.14)

–статическое отклонение от силы , т.е.

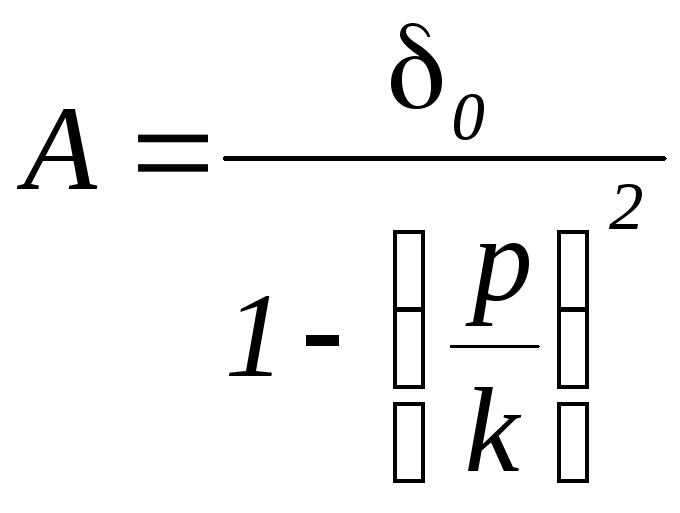, т.е. амплитуда зависит от отношения частоты возмущающей силы к частоте собственных колебаний.

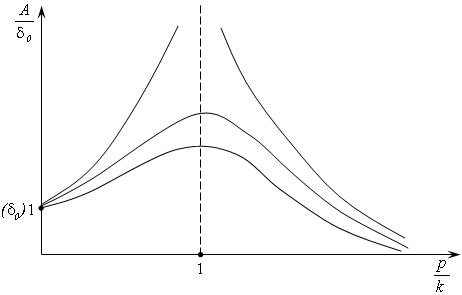
Рис. 5.2

Если стремится к нулю (или), тогда амплитуда колебания стремится к, т.е. отношение.

Если близко к, то амплитуда становится очень большой (рис. 5.2).

Если амплитуда становится очень малой (практически равной нулю) (рис. 5.2).