Теорема моментов относительно оси

Рассмотрим материальную точку М массой m, движущуюся под действием силы (рис. 9.1).

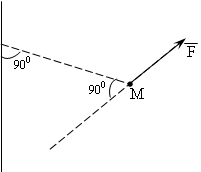
Рис. 9.1

Известно, что момент силы относительно центра равен

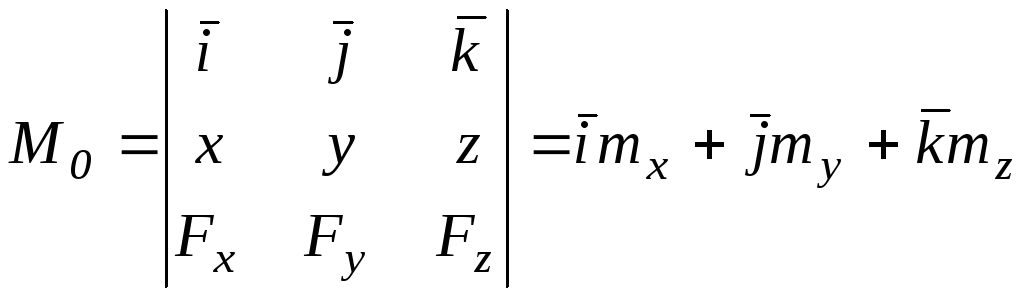, (9.1)

где – момент силыотносительно центра О;

– моменты силыотносительно осей х, у,z.

Например, для оси z момент силы будет:

, (9.2)

Аналогично для вектора можно записать:

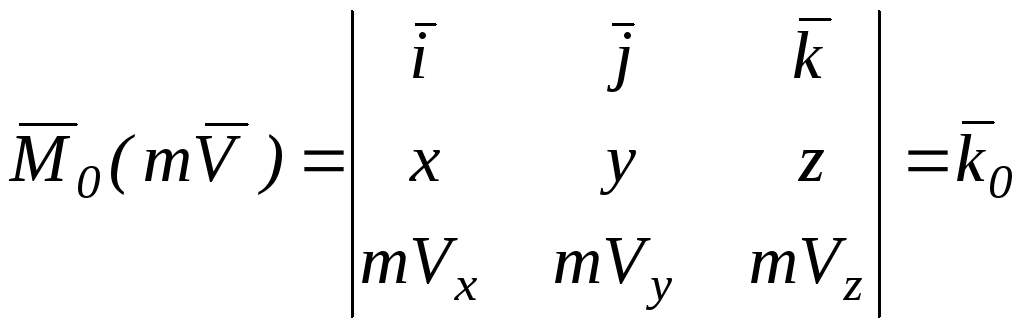, (9.3)

или: , (9.4)

где – проекции вектора момента количества движения на оси координат.

, (9.5)

Дифференцируя обе части выражения по времени, получим:

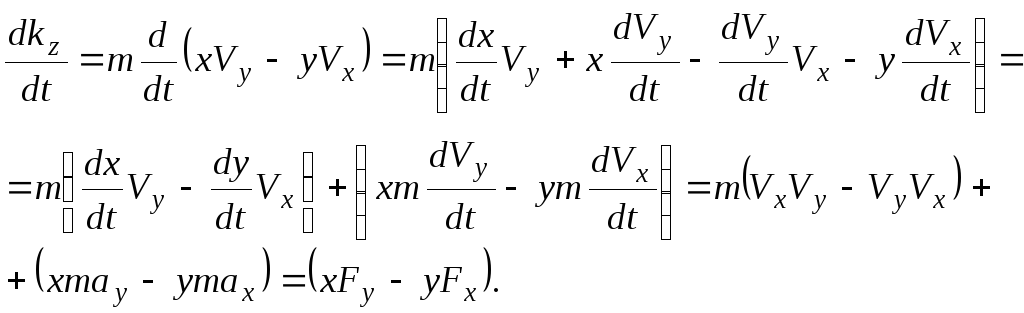
Так как и.

В итоге получим:

, (9.6)

Сравнивая выражения (9.2) и (9.6), получим:

, (9.7)

Таким образом, производная по времени от момента количества движения точки относительно какой-нибудь оси равна моменту действующей силы относительно той же оси.

Теорема моментов относительно центра

Пусть материальная точка массой m движется под действием силы . Так как момент силы будет равен:

,

то аналогично для вектора момент будет:

, (9.8)

Дифференцируя это выражение по времени t, получим:

.

Так как , то:

, т.е.:

, (9.9)

Производная по времени от момента количества движения взятого относительно какого-нибудь центра равна моменту действующей на точку силы относительно того же центра.

Задачи с помощью теоремы об изменении момента количества движения материальной точки рекомендуется решать в следующей последовательности:

1. выбрать систему координат (при движении точки по дуге окружности следует одну из осей направить через центр окружности перпендикулярно к ее плоскости);

2. изобразить на рисунке силы, приложенные к материальной точке, т.е. активные силы и реакции связей (применив закон освобождаемости от связей);

3. вычислить суммы моментов сил, приложенных к материальной точке, относительно осей координат;

4. изобразить вектор количества движения материальной точки, записать выражение его моментов относительно неподвижных осей координат и взять от них производные по времени;

5. подставить результаты расчетов двух предыдущих пунктов решения задачи в уравнения теоремы об изменении момента количества движения материальной точки;

6. решить, в соответствии с условием, прямую либо обратную задачу динамики точки.

Задача 9.1 (28.4)

Гирька М привязана к концу нерастяжимой нити МОА, часть которой ОА пропущена через вертикальную трубку. Гирька движется вокруг оси трубки по окружности радиуса МС=R, делая 120 об/мин. Медленно втягивая нить ОА в трубку, укорачивают наружную часть нити до длины ОМ₁, при которой гирька описывает окружность радиусом 1/2R. Сколько оборотов в минуту делает гирька по этой окружности.

Решение

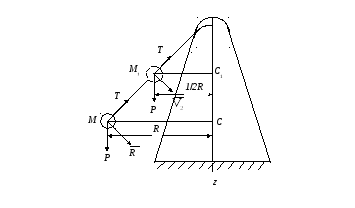
Рис. 9.2

На рис. 9.2 представлено схематично условие задачи. Для решения задачи применим теорему об изменении момента количеств движения для материальной точки.

На гирю действуют силы: - сила тяжести,- сила натяжения нити. Моменты этих сил относительно осиz будут равны нулю, так как сила параллельна осиz, а сила пересекает осьz.

Тогда

где K_z – момент количеств движения гирьки относительно оси z.

Так как , то. Отсюда следует, что. Это означает, что при вращении гирьки вокруг осиz при изменении длины нити момент количеств движения остается постоянным.

Для положения гирьки в точке М момент количеств движения относительно оси z будет:

, где ,- угловая скорость вращения гирьки в положенииМ.

Для положения гирьки в точке ' момент количеств движения относительно оси z будет:

, где ,- угловая скорость вращения гирьки в положенииМ₁.

Так как момент количеств движения гирьки не изменяется, то . Отсюда следует, что.

По условию задачи , тогда.

, отсюда: .

Подставив численные значения, получим: об/мин.

Ответ: n₂ = 480 об/мин.