Момент инерции тела относительно оси. Радиус инерции.

Моментом инерции тела (системы) относительно данной оси O_z (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояния от этой оси:

, (6.6)

При вращательном движении осевой момент инерции играет такую же роль, какую масса при поступательном, т.е. осевой момент инерции является мерой инертности тела при вращательном движении.

При пространственном распределении материальных тел моменты инерции относительно осей координат будет (рис. 6.1):

; ;, (6.7)

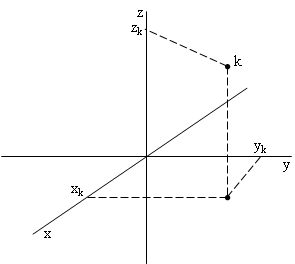
Рис. 6.1

Радиусом инерции тела относительно оси O_z называется линейная величина , определяемая равенством:

, (6.8)

где – масса тела.

Моменты инерции некоторых однородных тел

1. Тонкий однородный стержень длинной и массой.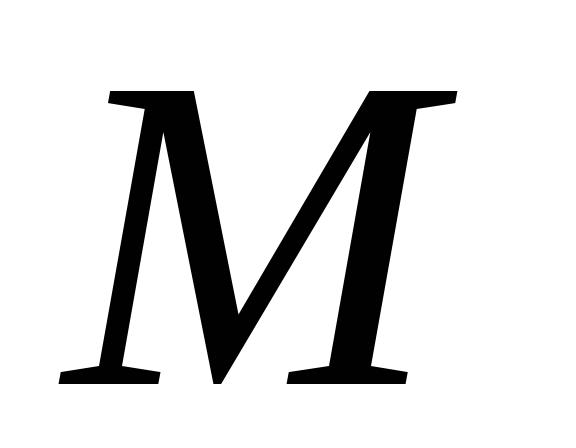

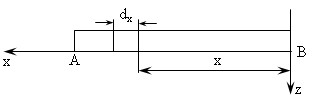
Рис. 6.2

Вычислим момент инерции однородного стержня длинной и массойотносительно оси, проходящей через торец В перпендикулярно его длине (рис. 6.2). Тогда для любого элементарного отрезка длинына расстоянии х от осиz масса будет . Тогда для элементарного отрезкамомент инерции будет:

,

где , где, откуда:

,

интегрирование этого выражения дает:

.

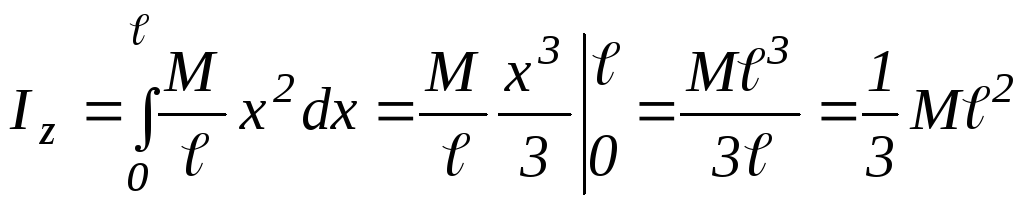Таким образом, момент инерции стержня относительно оси, проходящей перпендикулярно через его конец, будет:

.

2. Тонкий однородный диск радиусом и массой.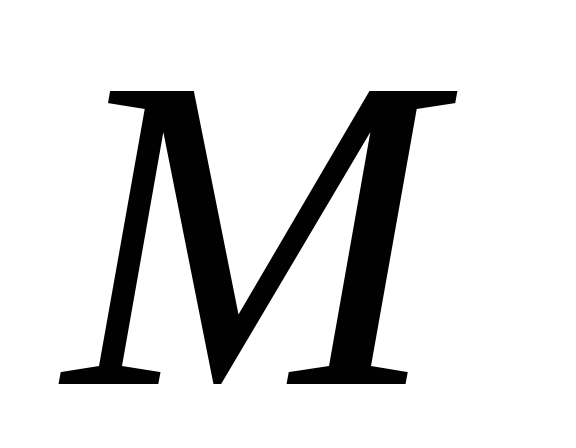

Найдем его момент инерции относительно оси O_z перпендикулярной плоскости диска и проходящей через его центр (рис. 6.3).

Рис. 6.3

Выделим элементарное кольцо шириной на расстояниеот центра (осиZ).

; ,

где .

Тогда: ,

где .

Тогда: .

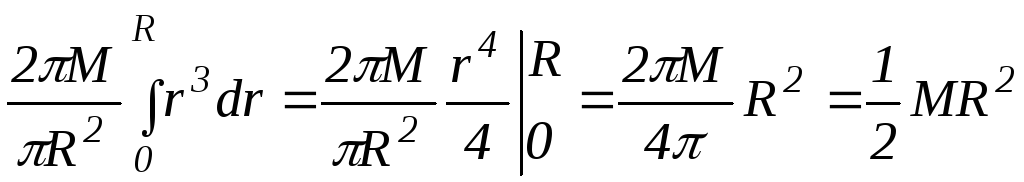Момент инерции относительно параллельных осей. Теорема Гюйгенса

Момент инерции тела относительно данной оси равен моменту инерций относительно оси, ей параллельной, проходящей через центр масс тела, сложенному с произведением массы всего тела на квадрат расстояния между осями (рис. 6.4):

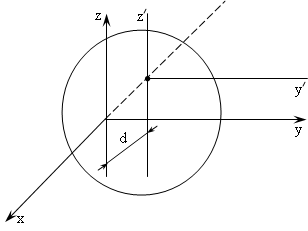
Рис. 6.4

Задача 6.1

Определить момент инерции тонкого однородного стержня относительно оси CZ, перпендикулярной оси и проходящей через его центр масс (рис. 6.5).

Решение

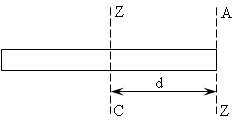
Рис. 6.5

Так как ось CZ проходит через центр масс, то:

, откуда

.

В данном случае , где– длина стержня.

,

Тогда .

Ответ: .

Задача 6.2 (34.9)

Вычислить момент инерции тонкого однородного полудиска массой m и радиуса r относительно оси, проходящей вдоль диаметра, ограничивающего полудиск (рис. 6.6)

Решение

Выделим в полудиске элементарный слой толщиной dk и высотой y на расстоянии x от начала координат. Для элементарного слоя элементарный момент инерции будет:

, (1)

Элементарная масса равна:

,

где dS – площадь элементарного слоя dS=2ydx, тогда:

dm=ρ2ydx,

где ρ – поверхностная плотность, равная ;

S – площадь полудиска, равная .

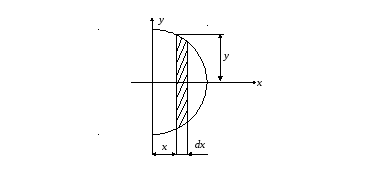
Рис. 6.6

Тогда .

Подставляя это выражение в уравнение (1) получим:

.

Так как уравнение окружности: , то:.

Тогда:

.

Интегрируя это выражение, получим:

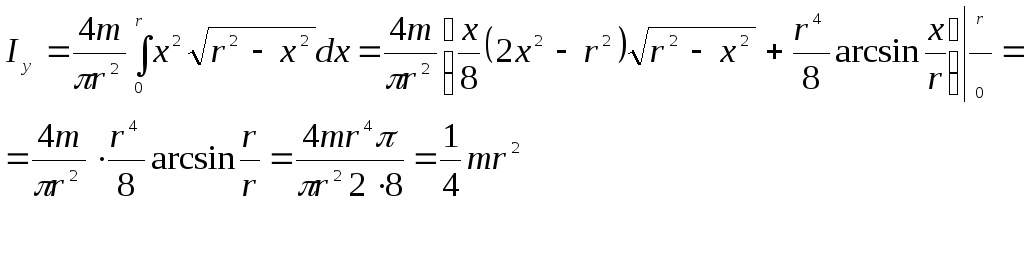
Ответ: .

Задача 6.3 (34.10)

Вычислить осевые I_x и I_y моменты инерции изображенной однородной прямоугольной пластины массой m относительно осей x и y (рис.6.7).

Решение

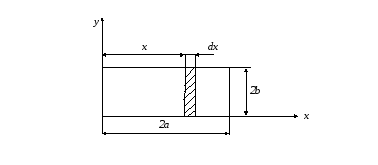
Рис. 6.7

Выделим элементарный участок шириной dx на расстоянии x от начала координат. Тогда момент инерции (dI_y) элементарного участка будет:

где dm – масса элементарного участка.

dm=ρds=ρydx,

Тогда .

Проинтегрируем это выражение:

.

Так как y=2b, то:

Поверхностная плотность , тогда:

.

Ответ: .