Задача 4.1 (32.4.)

Груз Q, падая с высоты м без начальной скорости, ударяется об упругую горизонтальную балку в ее середине; концы балки закреплены. Написать уравнение дальнейшего движения груза на балке, отнеся движение к оси, проведенной вертикально вниз из положения статического равновесия груза на балке, если статический прогиб балки в ее середине при указанной нагрузке равен 0,5 см; массой балки пренебречь.

Решение

Рис. 4.3

Направим ось х по вертикали вниз, взяв за начало отсчета О положение статического равновесия груза (рис. 4.3). В положении статического равновесия балка прогибается на величину статического равновесия , гдеС – коэффициент упругости балки.

Рассмотрим груз в положении, смещенном относительно нуля на х вниз и предположим, что груз движется вниз в сторону возрастания х. Балка прогибается и ее сила упругости ,

где: δ – смещение середины балки из ненагруженного состояния, т.е. , тогда

.

Кроме силы к грузу приложена сила тяжести.

Составим уравнение движения груза под действием данных сил:

.

Проектируя это векторное уравнение на ось х, получим:

, или

. (1)

Учитывая, что в состоянии равновесия: или в проекции на ось х, получим, где, тогда

. (2)

Учитывая это, выражение (1) примет вид:

, или

Обозначим , тогда. (3)

Для решения этого дифференциального уравнения второго порядка составим соответствующее характеристическое уравнение:

, отсюда

.

Так как корни мнимые и различные, то решением уравнения (3) будет:

. (4)

Определим численное значение :

.

Так как из уравнения (2) следует, что , тогда

(с^-1).

с^-1

Тогда уравнение (4) примет вид:

. (5)

Постоянные С₁ и С₂ определим из начальных условий: при , а так как груз падает с высотыh, то начальную скорость можно определить следующим образом.

При падении груза с высоты h, конечная скорость будет:

, так как груз падает без начальной скорости, т.е. , то

, отсюда

Так как ,, тогда

, отсюда .

Подставляя численные значения, получим: (м/с)

м/с.

Конечная скорость груза при падении является начальной скоростью движения середины балки (), тогда

м/с

Подставляя в уравнение (5) полученные условия, получим:

; или .

при , получим:, или(м).

м.

Тогда уравнение движения (5) примет вид:

(м)

Ответ: (м).

3. Свободные колебания при сопротивлении, пропорциональном скорости (затухающие колебания)

Пусть на материальную точку М массой m действуют восстанавливающая сила и сила сопротивления(Рис.4.4). Дифференциальное уравнение движения будет:

.

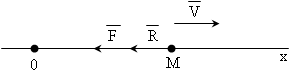
Рис. 4.4

Разделив обе части уравнения на массу, получим:

, (4.8)

где ;.

Уравнение (1) представляет собой дифференциальное однородное уравнение второго порядка. Для его решения составим соответствующее характеристическое уравнение:

. (4.9)

4. Рассмотрим случай, когда k>b, т.е. сопротивление мало по сравнению с восстанавливающей силой.

Пусть , тогда, как следует из выражения (2), корни характеристического уравнения будут комплексными. В этом случае решение уравнения (1) ищем в виде:

, (4.10)

где с₁ и с₂ – постоянные коэффициенты, определяемые по начальным условиям. Делая замену: ии тригонометрические преобразования, получим:

. (4.11)

Колебания, происходящие по закону (4.8) называются затухающими (рис.4.5).

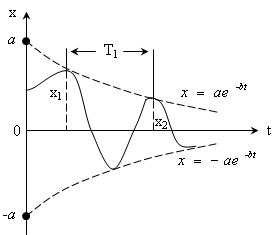
Рис. 4.5

Период затухающих колебаний определяется по формуле:

, (4.12)

Величина, равная отношению двух амплитуд, различающихся на величину периода колебания, называется декрементом колебаний:

, (4.13)

Прологарифмировав это выражение, получим:

, (4.14)

Величина, равная , называется логарифмическим декрементом затухания.

5. Рассмотрим случай, когда b>k, т.е. сила сопротивления велика по сравнению с восстанавливающей.

Обозначим , тогда корни квадратного уравнения (4.12) будут действительные и отрицательные. В этом случае решение уравнения (1) ищем в виде:

, (4.15)

График такого движения показан на рис. 4.6

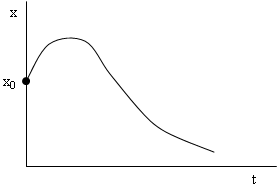
Рис. 4.6

Движение, совершаемое материальной точкой по закону, описываемое уравнением (4) является периодическим, так как описывается периодической функцией, т.е. это колебательный процесс. Так как амплитуда колебания с течением времени асимптотически приближается к статическому положению равновесия, то это затухающие колебания. Действительно найдем предел, к которому стремится функция в уравнении (4) при увеличении времени:

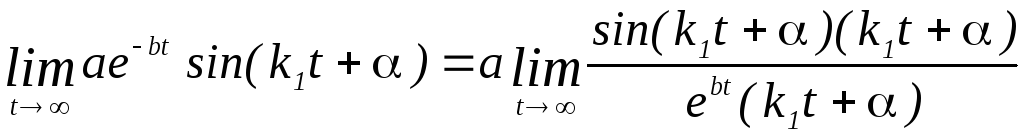, (4.16)

Учитывая, что (первый замечательный предел),

то 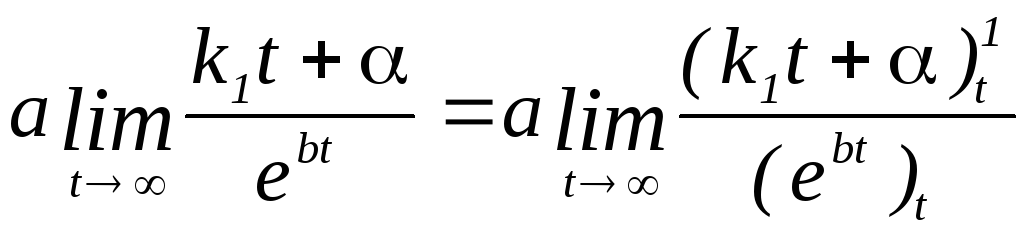(примем правило Лопиталя), получим, что. Это означает, что амплитуда колебания асимптотически стремится к нулю.

3. Рассмотрим случай, когда k<b, т.е. сила сопротивления больше восстанавливающей силы. В этом случае в уравнении (2) дискриминант будет положительным, т.е.

, пусть .

В этом случае корни характеристического уравнения (4.12) будут действительные и отрицательные: ;. Тогда решение уравнения (1) будет иметь вид:

(4.17)

Проанализируем это выражение. Движение, описываемое уравнением (5) не является периодическим, так как входящие в нее экспоненциальные функции – не периодические. Это движение затухающее, так как отклонение точки от положения статического равновесия с течением времени приближается к нему, т.е. . Действительно:

.

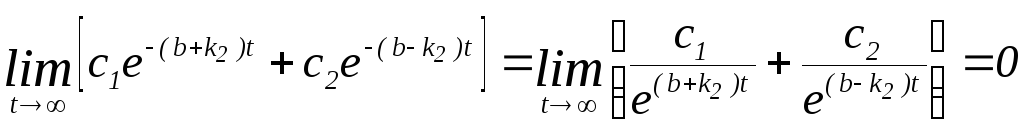Иными словами это движение является затухающим. На рис. 4.7 представлены графики – это движения в зависимости от начальных условий.

а) , т.е. направление скорости совпадает с возрастанием отклонения.

б) , т.е. направление скорости противоположно направлению оси х и не очень большая.

в) , т.е. направление скорости противоположно направлению оси х и больше по величине.

Во всех случаях а, б, в движения будут затухающими и непериодическими.

Рис. 4.7

6. Рассмотрим случай, когда 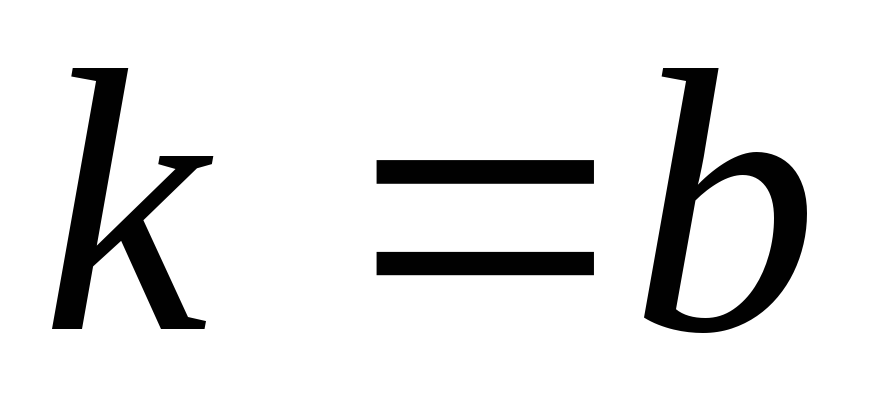, тогда корни характеристического уравнения (2) будут равны и отрицательны. Поэтому решение уравнения (1) ищем в виде:

. (4.18)

Движение, описываемое уравнением (6), является непериодическим, так как включает линейную и экспоненциальные функции и затухающим, т.е. .