Задача 2.4. (27.2)

Тяжелое тело спускается по гладкой плоскости, наклоненной под углом 30⁰ к горизонту. Найти, за какое время тело пройдет путь 9,6 м, если в начальный момент его скорость равнялась 2 м/с.

Решение

Рис. 2.5

На рис. 2.5. схематично представлено движение груза по наклонной плоскости. На тело действуют силы: – сила тяжести груза,– сила реакции опоры, так как поверхность гладкая по условию задачи, то силой трения пренебрежем. Выберем за начало движения исходное положение груза на наклонной плоскости (точка 0), осьх направим в сторону движения груза.

Составим дифференциальное уравнение движения груза по наклонной плоскости:

.

Спроектируем это векторное уравнение на ось х:

. (1)

Здесь учтено, что проекция ускорения равна по модулюa, так как ускорение груза направлено вдоль оси х.

Из уравнения (1) следует, что

. (2)

Уравнение (2) представляет дифференциальное уравнение с разделяющимися переменными:

.

Интегрируя это выражение, получим:

,

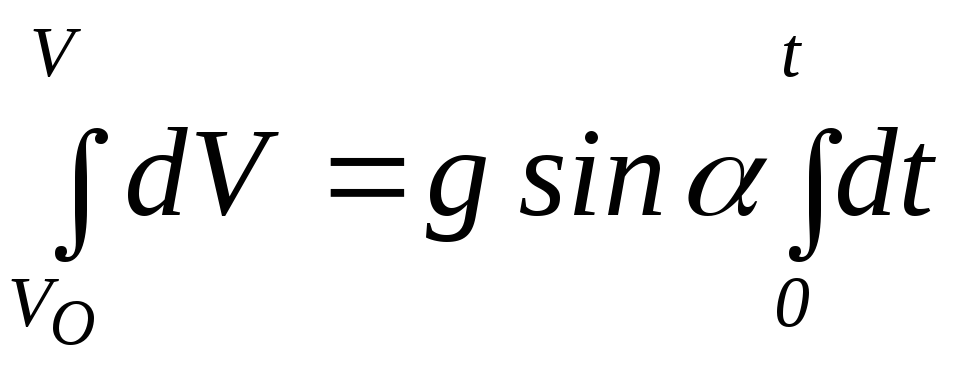где V₀ – скорость груза в начальный момент времени.

Отсюда следует, что

, или

, так как , то

.

Это дифференциальное уравнение первого порядка с разделяющимися переменными:

Интегрируя это выражение, получим:

.

Отсюда следует, что:

.

Подставляя исходные данные: V₀ = 2 м/с, х = 9,6 м и преобразовывая, получим:

.

Решая это квадратное уравнение, получим:

.

Отсюда t₁ = -2,4 t₂ = 1,6, так как время может быть только положительным, поэтому выбираем t = 1,6 с.

Ответ: t = 1,6 с.

2. Криволинейное движение точки

Рассмотрим свободную материальную точку, движущуюся под действием сил ,, …. Выберем неподвижную систему координатo x y z (рис. 2.6.)

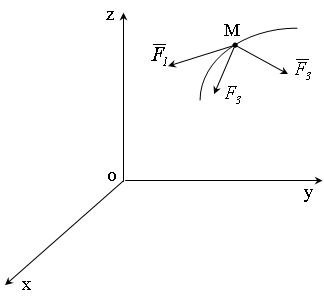
Рис. 2.6.

Составим уравнение движения точки:

. (2.8)

Спроектируем векторное уравнение на оси координат:

; ;, (2.9)

Учитывая, что ;;, получим дифференциальные уравнения криволинейного движения точки.

; ;. (2.10)

Уравнения (2.10) позволяют решать как первую, так и вторую задачи динамики.

Начальные условия задаются в виде: при t = 0

x = x₀, y = y₀, z = z₀

V_x = V_xo, V_y = V_yo, V_z = V_oz

Задача 2.5 (27.52)

Тело весом Р, брошенное с начальной скоростью V₀ под углом α к горизонту, движется под влиянием силы тяжести и сопротивления R воздуха. Определить наибольшую высоту h тела над уровнем начального положения, считая сопротивление пропорциональным первой степени скорости: .

Решение.

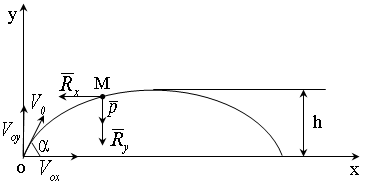
Рис. 2.7

Выберем систему координат с центром в точке начала движения тела (рис. 2.7). Рассмотрим силы, действующие на тело в произвольном положении в точке М траектории: – сила тяжести тела;и– силы сопротивления по осяму и х. Тогда уравнения движения тела будут:

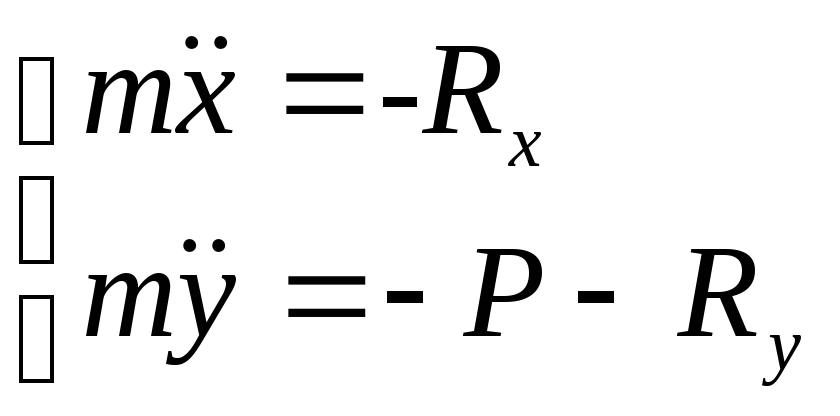(1), (2)

Так как нас интересует наибольшая высота подъема тела, то рассмотрим вертикальную составляющую движения тела:

, или

Разделяя переменные в этом дифференциальном уравнении первого порядка, получим:

. (3)

Так как: ;, тогда подставляя эти выражения в дифференциальное уравнение (3), получим:

. (4)

Интегрируя уравнение (4), получим:

;

;

.

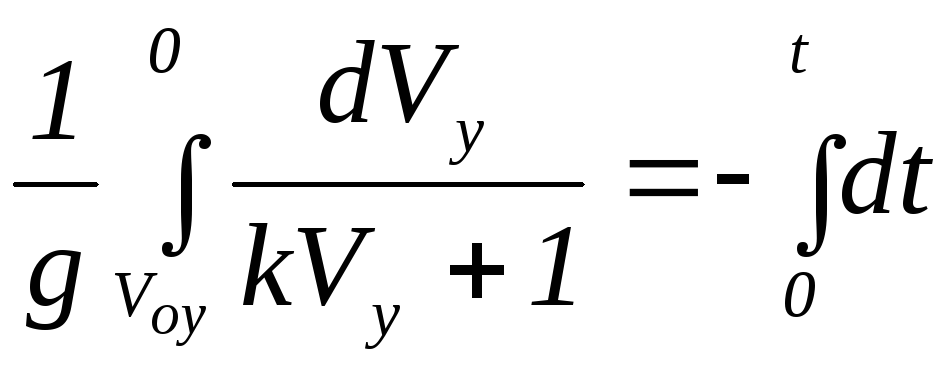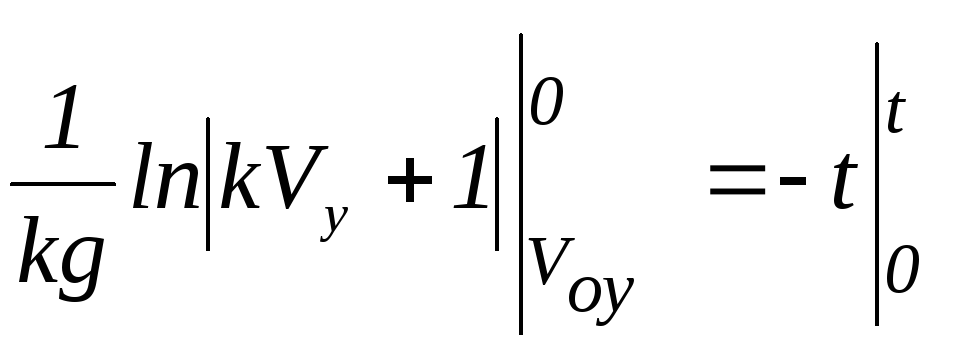После преобразований получим:

.

Так как , то

. (5)

Определим уравнение движения тела в вертикальном направлении. Воспользуемся уравнением (2):

Отсюда следует, что , т.е.

, или

. (6)

Это дифференциальное уравнение второго порядка, неоднородное. Решение уравнения (6) представим в виде:

где у₁ – общее решение однородного дифференциального уравнения;

у₂ – частное решение однородного дифференциального уравнения.

– однородное дифференциальное уравнение, составим соответствующее характеристическое уравнение:, отсюда. Поэтому;. Тогда решениеу₁ имеет вид:

.

Решение у₂ ищем в виде:

,

так как одним корнем характеристического уравнения есть ноль, тогда:

, , отсюда при подстановке этих выражений в уравнение (6), получим:

, или .

Тогда , поэтому

.

По начальным условиям: t₀ = 0; x₀ = 0; V_oy = V_oy, следует:

С₁ + С₂ = 0, т.е. С₁ = – С_{2 ,}

, или подставляя начальные условия, получим:

, отсюда .

Тогда , поэтому

,

после преобразований, получим:

. (7)

(7) является уравнением движения тела в вертикальном направлении.

Верхней точки траектории тело достигает за время, определяемое выражением (5), тогда с учетом, что , получим, что наибольшая высота поднятия тела:

. (8)

Так как по определению логарифма числа: , то выражение (8) преобразуется:

.

Отсюда следует, что:

.

Ответ: наибольшая высота поднятия тела равна:

.