Вопросы для самоконтроля:

1. Что такое момент количества движения точки и механической системы?

2. Теорема об изменении момента количества движения материальной точки и механической системы?

Задачи, рекомендуемые для самостоятельного решения: 28.4. – 28.20, 37.1 – 37.59. [3].

Литература: [1] – [5].

Лекция 10

1. Теорема об изменении кинетической энергии материальной точки и механической системы

Рассмотрим материальную точку массой m перемещающуюся из положения М₀, где она имеет скорость V₀ в положение М₁, где она имеет скорость V₁. Согласно второго закона Ньютона:

, (10.1)

Спроектируем обе части уравнения на направление касательной к точке М:

, (10.2)

Вектор можно представить в виде:

.

Тогда: .

Разделяя переменные, получим:

.

Интегрируя это выражение, получим:

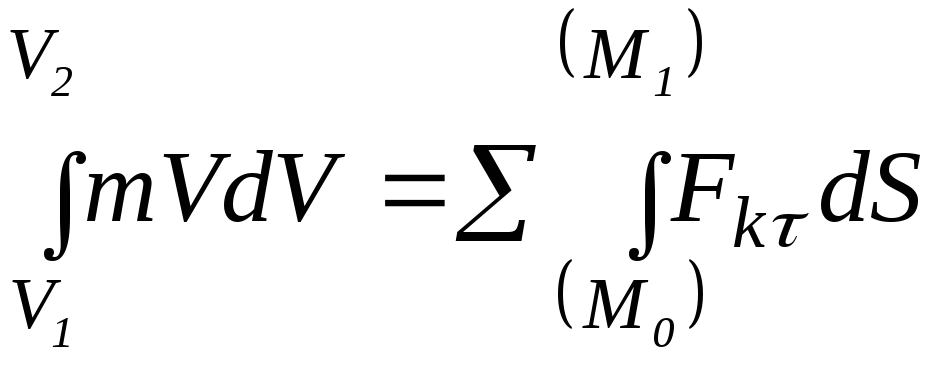, тогда:

, (10.3)

Выражение называется кинетической энергией точки массойm, движущейся со скоростью V и обозначается Т, т.е.:

, (10.4)

Кинетическая энергия измеряется в Джоулях.

Таким образом, изменение кинетической энергии точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.

Решение задач с помощью теоремы об изменении кинетической энергии материальной точки рекомендуется проводить в такой последовательности:

1. изобразить на рисунке силы, приложенные к материальной точке, т.е. активные силы и реакции связей;

2. вычислить сумму работ всех сил, приложенных к материальной точке, на ее перемещения;

3. вычислить кинетическую энергию материальной точки в ее начальном и конечном положениях;

4. использовав результаты вычислений двух предыдущих пунктов, применить теорему об изменении кинетической энергии материальной точки и определить искомую величину.

Задача 10.1 (30.1)

Тело Е, масса которого равна m, находится на гладкой горизонтальной плоскости. К телу прикреплена пружина жесткостью С, второй конец которой прикреплен к шарниру О₁. Длина недеформированной пружины равна l₀; ОО₁=l. В начальный момент тело Е отклонено от положения равновесия О на конечную величину ОЕ=а и отпущено без начальной скорости. Определить скорость тела в момент прохождения положения равновесия.

Решение

a

l

O

O₁

E

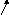
Рис. 10.1

На рис. 10.1. представлено схематично тело Е, скрепленное с пружиной. Применим теорему об изменении кинетической энергии материальной точки:

, (1)

где: - изменение кинетической энергии тела при переходе из положения в точкеЕ в точку О, т.е. ;Т₀ – кинетическая энергия тела в положении Е; Т₀=0, так как в этом положении скорость тела равна нулю; Т₁ – кинетическая энергия тела в положении О, , гдеV – скорость тела в положении О.

- сумма работ внешних сил.

На тело действуют силы: - сила тяжести;- сила реакции опоры;- сила упругости пружины (рис. 10.1).

Так как тело Е перемещается по горизонтальной плоскости, то работа сил ибудет равна нулю, поэтому:

, (2)

где: А_y – работа силы упругости пружины при изменении длины при переходе из положения Е в положение О. Тогда:

, (3)

где: - начальное удлинение пружины;

- конечное удлинение пружины;

, , (4)

Подставляя выражение (4) в уравнение (3) получим:

, (5)

Подставляя уравнение (5) в уравнение (1) получим:

, (6)

Отсюда

Ответ: .