Задача 7.1

К призме 3 массой прикреплены блоки А и В радиусоми, через которые перекинуты нити, к концам которых прикреплены грузы 1 и 2 массами соответственнои. Груз 1 спускается по закону. Определить нормальное давление призмы 3 на горизонтальный пол.

Решение

а) б)

Рис. 7.1

На систему, состоящую из призмы 3 и грузов 1 и 2, действуют силы: – сила тяжести груза 1;– сила тяжести груза 2;– сила тяжести груза 3;– сила реакции системы на плоскость.

Выберем систему координат ХУ с началом в точке О (рис. 7.1).

Для решения задачи используем теорему о движении центра масс системы:

, (1)

где – масса системы;

– ускорение центра масс системы.

С учетом того, что:

, (2)

где – ускорения центров масс тел системы.

Проектируя векторные уравнения (1) и (2) на ось у, получим:

, (3)

Пусть , или

, (4)

, (5)

–представляют смещения центров масс тел системы при перемещении груза 1 по наклонной плоскости.

Перемещение груза 1 по наклонной плоскости из начального положения («0») в конечное («1») составляет , а смещение центра масс груза по оси у составляет у₁, равное:

,

так как , то

, (6)

При перемещении груза 1 по наклонной плоскости на расстояние , блок, радиусомповернется на угол, равный:

.

При этом перемещении груза 2 по вертикали, равное у₂ определится:

,

, (7)

Тогда: ;;

; .

Так как движение грузов 1 и 2 не вызывает изменение центра масс призмы 3, то: ,.

Подставляя выражения (6) и (7) в уравнение (5), получим:

.

Отсюда следует, что:

.

Сила нормального давления (R) призмы 3 на горизонтальный пол будет приложена к полу и направлена в противоположную сторону и по модулю равна силе нормальной реакции N, т.е.:

.

Ответ: Сила давления призмы на горизонтальный пол равна .

Вопросы для самоконтроля:

1. Что такое центр масс механической системы?

2. Свойства суммы внутренних сил?

Задачи, рекомендуемые для самостоятельного решения: 35.1. – 35.22. [3].

Литература: [1] – [5].

Лекция 8

1. Теорема об изменении количества движения материальной точки

Количеством движения называется векторная величина , равная произведению массы точки на вектор ее скорости.

Направлен вектор так же, как и скорость точки, т.е. по касательной к ее траектории.

Вектор количества движения обозначим через , тогда:

, (8.1)

Импульс силы. Элементарным импульсом силы называется векторная величина , равная произведению вектора силына элементарный промежуток времени:

, (8.2)

Направлен элементарный импульс по линии действия силы.

За конечный промежуток времени импульс силы определяется по формуле:

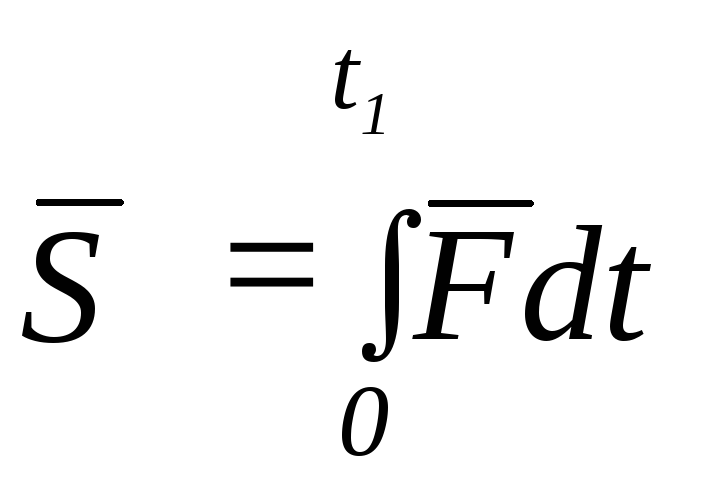, (8.3)

Проекции импульса силы на оси координат будут:

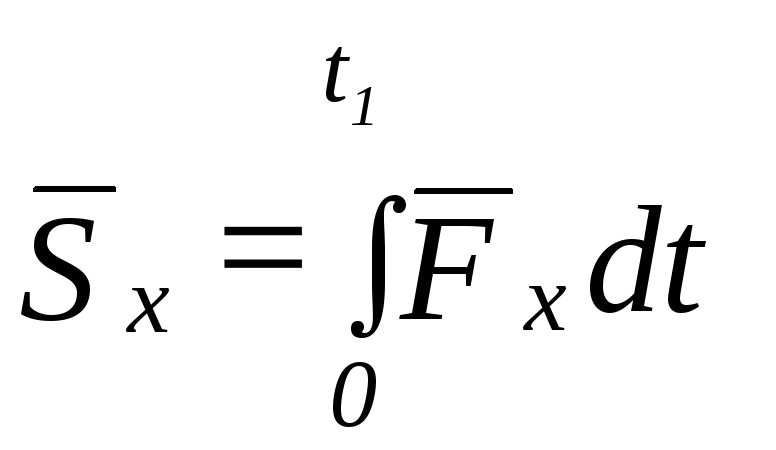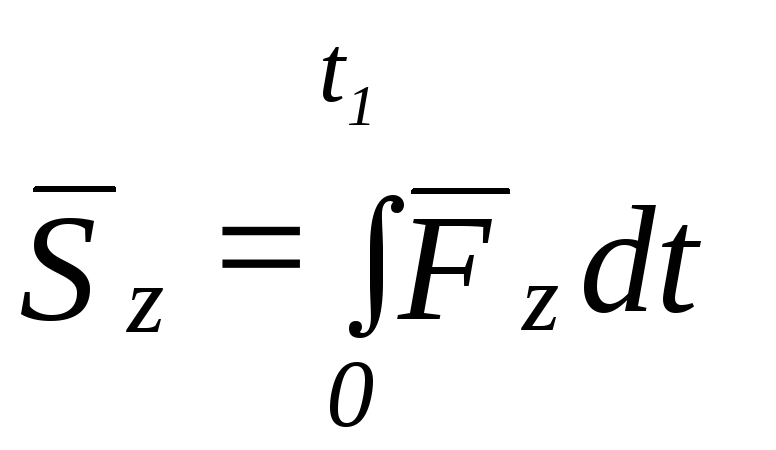, ,, (8.4)

Теорема об изменении количества движения точки в дифференциальной форме

Производная по времени от количества движения точки равна геометрической сумме действующих на точку сил:

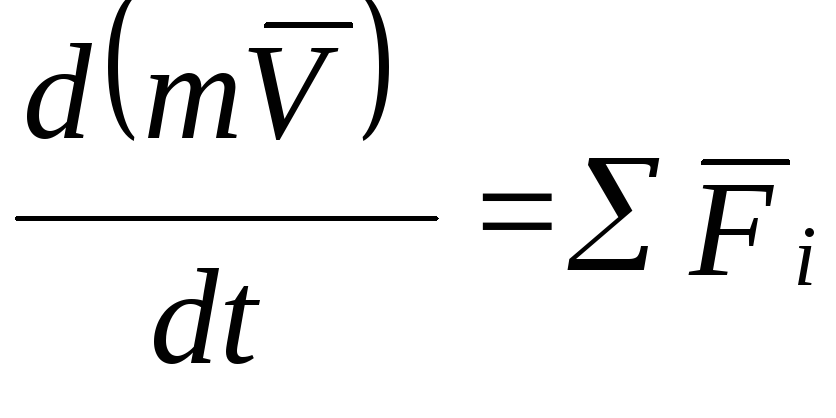, (8.5)

Теорема об изменении количества движения материальной точки в интегральной форме:

, (8.6)

Изменение количества движения точки за некоторый промежуток времени равно геометрической сумме импульсов всех действующих на точку сил за тот же промежуток времени.

В координатной форме уравнение (8.6) примет вид:

(8.7)

.

Рекомендуется следующая последовательность решения задач на применение теоремы об изменении количества движения материальных точек:

1. изобразить на рисунке все силы, приложенные к материальной точке, т.е. активные силы и реакции связей (применить закон освобождаемости от связей);

2. выбрать систему координат;

3. записать теорему об изменении количества движения материальной точки (системы) в проекциях на эти оси:

;

;

.