
big_doc_LKG
.pdf

Оцінка стохастичних зв’язків між вхідними та вихідними ознаками 249
, (5.9)
де  ,
,  – середини відповідних інтервалів по осях
– середини відповідних інтервалів по осях  ,
,  .
.
Матеріал групують по інтервалах значень величин  та
та  , потім складають кореляційну таблицю (табл. 5.1), у якій також здійснюють розрахунок частот.
, потім складають кореляційну таблицю (табл. 5.1), у якій також здійснюють розрахунок частот.
Таблиця 5.1 Кореляційна таблиця для визначення щільності зв’язку
Інтервал |
|
|
Інтервали x |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коефіцієнт кореляції можна визначити за такими формулами:
; |
(5.10) |
; |
(5.11) |
; |
(5.12) |


Оцінка стохастичних зв’язків між вхідними та вихідними ознаками 251
то дисперсія всього ряду буде дорівнювати сумі внутрішньогрупової
і міжгрупової дисперсій.
Загальна дисперсія визначає середній квадрат відхилень (за орди-
натою) точок кореляційного поля від лінії |
(рис. 5.3) |
|
|
. |
(5.15) |
Дисперсія  визначає середній квадрат відхилень точок кореляційного поля від емпіричної лінії
визначає середній квадрат відхилень точок кореляційного поля від емпіричної лінії
|
|
, |
(5.16) |
де |
|
– середнє арифметичне значення |
в i-му |
|
|
інтервалі по осі . |
|
Ця складова характеризує ступінь розсіяння змінної |
навколо |
||
групових середніх |
, тобто описує вплив випадкових факторів на |
||
результати спостереження або досліду, незалежних від . |
|
||
Дисперсія |
|
описує вплив досліджуваного фактора |
на зміну |
функції |
і представляє середній квадрат відхилень емпірич- |
||
ної лінії регресії від лінії |
|
||
|
|
. |
(5.17) |
Емпіричне кореляційне відношення розраховують за формулою
. (5.18)
Величина  змінюється в межах
змінюється в межах  .
.


Оцінка стохастичних зв’язків між вхідними та вихідними ознаками 253
Підтвердження гіпотези означає, що обчислений за формулами (5.3), (5.10)–(5.13) вибірковий коефіцієнт кореляції є значимим.
Перевірку прийнятої гіпотези можна здійснити двома способами.
Перший спосіб. Перевірка здійснюється за t-критерієм Стьюдента. Значення  обчислюється за формулою
обчислюється за формулою
 . (5.19)
. (5.19)
Величина 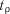 порівнюється з табличними значеннями
порівнюється з табличними значеннями  , визна-
, визна-
ченим за розподілом Стьюдента у відповідності з прийнятим рівнем значимості (зазвичай  ) і кількості ступенів вільності
) і кількості ступенів вільності  (додаток Д6).
(додаток Д6).
Якщо  , то отриманий коефіцієнт кореляції буде справед-
, то отриманий коефіцієнт кореляції буде справед-
ливим для всієї генеральної сукупності.
Якщо  , то у генеральній сукупності кореляції може не іс-
, то у генеральній сукупності кореляції може не іс-
нувати, або зв’язок є нелінійним.
Другий спосіб. Гіпотеза перевіряється порівнянням вибіркового значення коефіцієнта кореляції  з його критичним значенням
з його критичним значенням  , яке
, яке
являє собою  -квантиль розподілу
-квантиль розподілу  при
при  . Кореляція між випадковими величинами вважається значимою, якщо
. Кореляція між випадковими величинами вважається значимою, якщо  . Критичні значення
. Критичні значення  наведені у табл. 5.3.
наведені у табл. 5.3.
Для кореляційного відношення  перевірка нульової гіпотези
перевірка нульової гіпотези  :
:  проти альтернативної гіпотези
проти альтернативної гіпотези  :
:  виконується за допо-
виконується за допо-
могою статистики
|
|
|
, |
(5.20) |
де |
– кількість інтервалів факторіальної ознаки ; |
|
||
|
– загальна кількість спостережень результативної ознаки . |
|||
Отримане значення |
порівнюється |
з критичним |
значенням - |
|
критерію (додаток Д8) для вибраного рівня значимості |
і кількості |
|||
ступенів вільності |
та |
. |
|
|
Якщо |
, то нульова гіпотеза відхиляється на рівні значимості . |
|||

Оцінка стохастичних зв’язків між вхідними та вихідними ознаками 255
Ця статистика при справедливості нульової гіпотези має  -розподіл з
-розподіл з  та
та  ступенями вільності. Якщо
ступенями вільності. Якщо 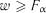 , то на рівні значимості
, то на рівні значимості  гіпотеза лінійності кореляційного зв’язку відхиляється.
гіпотеза лінійності кореляційного зв’язку відхиляється.
При другому підході міра нелінійності визначається за умовою
 . (5.22)
. (5.22)
У випадку  необхідно виміряти відхилення від лінійності. Це можна здійснити двома способами.
необхідно виміряти відхилення від лінійності. Це можна здійснити двома способами.
Перший спосіб. Цей спосіб полягає у порівняння різниці коефіцієнтів детермінації з деякою величиною параметра t, який визначається за формулою
 . (5.23)
. (5.23)
де t – коефіцієнт, за яким вимірюється відхилення від лінійності;
 – коефіцієнт детермінації, розрахований за емпіричним кореляційним відношенням;
– коефіцієнт детермінації, розрахований за емпіричним кореляційним відношенням;
 – коефіцієнт детермінації, розрахований за лінійним коефіцієнтом кореляції;
– коефіцієнт детермінації, розрахований за лінійним коефіцієнтом кореляції;
 – похибка різниці між
– похибка різниці між  та
та  . Величина
. Величина  визначається як
визначається як
|
, |
(5.24) |
де |
– коефіцієнт лінійності. |
|
Якщо величина |
то відмінність між емпіричною і теоретичною |
|
формами зв’язку вважають несуттєвою і кореляційний зв`язок визна-
ють лінійним.
Другий спосіб. Критерій прямолінійності зв’язку можна побуду-
вати на співвідношенні між |
та |
|
|
, |
(5.25) |


Оцінка стохастичних зв’язків між вхідними та вихідними ознаками 257
У системі координат (рис. 5.4) точками відмічаємо значення кожного спостереження і накреслюємо еліпс розсіяння.
y |
|
|
|
|
|
|
|
800 |
|
|
|
|
|
|
|
700 |
|
|
|
|
|
|
|
600 |
|
|
|
|
|
|
|
500 |
|
|
|
|
|
|
|
400 |
|
|
|
|
|
|
|
300 |
|
|
|
|
|
|
|
200 |
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
0 |
0,0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
x |
|
|
Рис. 5.4. Поле кореляції і еліпс розсіяння |
|
||||
Складаємо кореляційну таблицю (табл. 5.5). За формою еліпса розсіяння і табл. 5.4 робимо висновок, що між досліджуваними ознаками існує зворотний кореляційний зв’язок.
|
|
|
|
|
|
Таблиця 5.5 |
||
|
|
Кореляційна таблиця |
|
|
|
|||
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
ваг.-год. |
0–0,1 |
0,1–0,2 |
0,2–0,3 |
0,3–0,4 |
0,4–0,5 |
0,5–0,6 |
||
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 – 150 |
|
|
|
1 |
|
|
1 |
|
150 – 300 |
|
|
1 |
|
|
1 |
2 |
|
300 – 450 |
|
1 |
2 |
1 |
|
1 |
5 |
|
450 – 600 |
|
3 |
1 |
1 |
1 |
|
6 |
|
600 – 750 |
|
1 |
1 |
1 |
1 |
|
4 |
|
750 – 900 |
1 |
1 |
|
|
|
|
2 |
|
|
1 |
6 |
5 |
4 |
2 |
2 |
20 |
|
|
|
|
|
|
|
|
|
|
2. Кількісна оцінка щільності зв’язку. Оскільки вид зв’язку між змінними  та
та  невідомий, то необхідно обчислити за даними вибірки емпіричні значення коефі-
невідомий, то необхідно обчислити за даними вибірки емпіричні значення коефі-
цієнта кореляції та кореляційного відношення.
Розрахунок коефіцієнта кореляції. Розрахунок виконуємо за формулою (5.13).
Складові формули обчислюємо окремо в табл. 5.6.

 та
та  . Тоді кореляційне поле буде містити певну кількість клітин, у кожну з яких потрапляє деяка кількість експериментальних точок (рис. 5.3).
. Тоді кореляційне поле буде містити певну кількість клітин, у кожну з яких потрапляє деяка кількість експериментальних точок (рис. 5.3). інтервалів по
інтервалів по  та
та  інтервалів по
інтервалів по  , то математичні вирази для визначення коефіцієнта кореляції можна представити у більш зручному для практичних розрахунків вигляді:
, то математичні вирази для визначення коефіцієнта кореляції можна представити у більш зручному для практичних розрахунків вигляді: . (5.13)
. (5.13) маємо
маємо  збільшується
збільшується  ); при від`ємному
); при від`ємному  має місце
має місце  зменшується
зменшується  )
)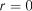 прямолінійна кореляція
прямолінійна кореляція  або
або  маємо прямолінійний
маємо прямолінійний  – зв’язок відсутній;
– зв’язок відсутній; – зв’язок слабкий;
– зв’язок слабкий; – зв’язок середній;
– зв’язок середній; – зв’язок сильний.
– зв’язок сильний.

 . За основу визначення щільності зв’язку у цьому випадку береться загальний показник мінливості досліджуваної функції – її повна дисперсія
. За основу визначення щільності зв’язку у цьому випадку береться загальний показник мінливості досліджуваної функції – її повна дисперсія – загальна дисперсія сукупності;
– загальна дисперсія сукупності;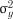 – дисперсія показника
– дисперсія показника  відносно емпіричної лінії регресії;
відносно емпіричної лінії регресії; – дисперсія лінії регресії відносно генерального середнього
– дисперсія лінії регресії відносно генерального середнього .
. спостережень включає
спостережень включає  груп спостережень,
груп спостережень, , що описує залежність між фак- тором-аргументом
, що описує залежність між фак- тором-аргументом  і залежною змінною
і залежною змінною  .
. і кореляційного відношення
і кореляційного відношення  , а також перевірку прийнятої гіпотези щодо лінійної форми кореляційного зв`язку.
, а також перевірку прийнятої гіпотези щодо лінійної форми кореляційного зв`язку. для
для  від нуля.
від нуля.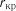 відносно нуля
відносно нуля



 :
: 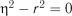 проти гіпотези
проти гіпотези  :
:  може бути виконана за допомогою статистики
може бути виконана за допомогою статистики . (5.21)
. (5.21) ) частки вантажів
) частки вантажів  , що прибувають в критих вагонах (ознака
, що прибувають в критих вагонах (ознака  ). Статистичні дані наведені в табл. 5.4.
). Статистичні дані наведені в табл. 5.4.
 .
. ,
,  .
.