28. Динамические ошибки в сау. Способы нахождения коэффициентов динамических ошибок.

Динамическими называются ошибки в замкнутой системе при входном воздействии вида

Этот сигнал относится к медленно меняющимся сигналам, так как (k+1) - ая производная этого сигнала по времени равна нулю.

Гармонический сигнал не является медленно меняющимся, так как ни одна из его производных не равна нулю.

Для определения динамической ошибки представим функцию рядом Тейлора, (6.3) где - неизвестные коэффициенты ошибки. Тогда=+...+. (6.4)

Этот ряд ограничен k-тым членом ряда, так какпри, поэтомупри.

Взяв от (6.4) обратное преобразование Лапласа, получим +...+, (6.5) где- символ дифференцирования.

В ряде (6.5) первое слагаемое называется ошибкой по положению, второе слагаемоеназывается ошибкой по скорости, а третье слагаемоеназывается ошибкой по ускорению.

Коэффициенты ,иназываются соответственно коэффициентами ошибки по положению, скорости и ускорению. Слагаемые более высокого порядка и входящие в них коэффициенты ошибокспециального названия не имеют.

29. Способы включения корректирующих звеньев.

Способы включения корректирующих звеньев для уменьшения ошибок в системе

Как было показано ниже, коэффициенты ошибок замкнутой системы полностью определяются коэффициентами передаточной функции. Для обеспечения требуемых значений коэффициентов ошибки в замкнутую систему дополнительно включают корректирующие звенья с передаточной функциейтакой, чтобы результирующая передаточная функцияобеспечила требуемые значения коэффициентов ошибки.

Для расширения возможностей физической реализуемости передаточных функций корректирующих звеньев их можно включать по трем схемам (рис.6.3):

- последовательно (а),

- параллельно (б),

- по схеме с обратной связью (в).

Рис.6.3 Способы включения корректирующих звеньев

При последовательной схеме соединений (рис.6.3.а) имеем: , где- передаточная функция исходной части схемы,W- желаемая для обеспечения малых ошибок передаточная функция. Тогда.

Но полученная по этой формуле функция физически может быть нереализуема. Тогда можно применить схему на рис. 6.3.б . Для того, чтобы обеспечить эквивалентность схем на рис. 6.3.а и 6.3.б , должно выполняться условие :, откуда выражение для передаточной функции корректирующего звена при параллельном способе включения будет иметь вид :, где.

Если и такой способ включения не решит проблему реализуемости функции , то можно применить схему на рис. 6.3.в . В этом случае должно выполняться условие :

, откуда, где.

Схема на рис. 6.3.в, кроме того, обеспечивает лучшую стабильность параметров звеньев, охваченных обратной связью.

30. Схема и особенности работы цифровых систем управления. Теорема отсчетов Котельникова-Найквиста. Достоинства и недостатки цсу

Теорема отсчетов Котельникова-Найквиста. Достоинства и недостатки цсу

Непрерывный сигнал может быть точно восстановлен по его отсчетам, если частота отсчетов более чем в 2 раза превышает верхнюю частоту в спектре этого сигнала.

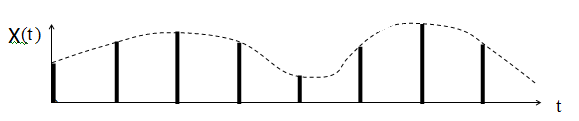
Найдем - время дискретизации:, где- частота дискретизации

По теореме Котельникова-Найквиста: ,,где,- полоса пропускания замкнутой системы.

33. Z - преобразование (прямое и обратное, примеры).Основные теоремы z - преобразования. Z - преобразование (прямое и обратное, примеры).

При большом числе разрядов АЦП цифровой сигнал x(n) эквивалентен дискретному сигналу , который представляется в виде последовательности взвешенных дельта-функций, площадь которых равна не единице, а значению непрерывного сигнала в моменты взятия отсчетов. Тогда, используя фильтрующее во времени свойство дельта-функций, запишем:(8.1) гдеn- номера отсчетов.

Возьмем преобразование Лапласа от сигнала (8.1): ===. (8.2)

По выражению (8.2) определяется дискретное преобразование Лапласа (ДПЛ) по отсчетам x(nT) из непрерывного сигнала. Однако для описания цифровых систем ДПЛ не нашло широкого применения из-за неудобства, связанного с частым повторением в формулах ДПЛ функции. От этого недостатка свободно Z - преобразование, которое следует из ДПЛ введением новой комплексной переменной.

Тогда из (8.2) имеем формулу прямого Z- преобразования для сигналаx(nT) . (8.3)

Сравнивая (8.2) и (8.3), видим, что формула для прямого Z- преобразования проще и компактнее формулы для прямого ДПЛ.

Примеры прямого Z- преобразования.

Единичный импульс

Аналогично для имеемX(p)=1.

Единичный дискретный скачок

=.

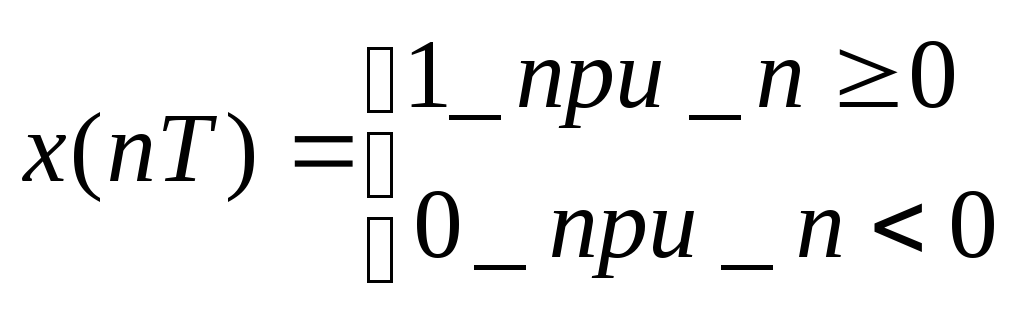
Аналогично для x(t)=1(t) имеемоткуда следует удобное для практики соответствие между переменной p в преобразовании Лапласа и переменной z в Z - преобразовании.

Наряду с прямым существует обратное Z- преобразование, которое определяется по выражению

=(8.4) где- вычетыX(z). Однократные вычеты определяются по формуле(8.5)

Выражение для X(z) в этой формуле следует представлять в следующем виде:

где ,- нули и полюсы функцииX(z) соответственно. В табл. 8.1 приведеныZ- преобразования наиболее характерных цифровых сигналовx(nT). Часто букву Т в описании этих сигналов опускают, полагая Т=1, т.е.x(nT)=x(n).

Дискретные функции и их Z- преобразования Таблица 8.1

см. прил.