21. Получение передаточных функций сложных сау.

На практике встречаются системы с двумя и более цепями обратной связи. Такие системы называются многоконтурными. На рис. 5.4 приведена схема двухконтурной системы.

Рис. 5.4 Схема двухконтурной системы

Передаточную функцию для этой системы получим поэтапно. Вначале получим выражение для передаточной функции внутреннего контура ВК, обведенного пунктиром. Схема ВК совпадает со схемой на рис. 5.3.б, для которой на основании получим:.

Теперь схема совпадает с рис. 5.3.а, в котором .

Отсюда на основании получим, гдеопределяется по приведенному выше выражению.

На рис. 5.5.а приведена схема трехконтурной системы, причем сигналы в цепи обратной связи берутся из разных точек схемы.

(а)

(б)

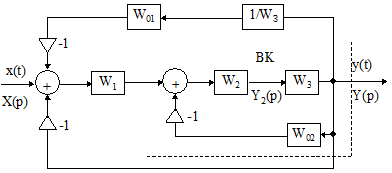
Рис. 5.5 Две эквивалентные схемы трехконтурной системы

На рис. 5.5.б приведена эквивалентная ей вторая схема, в которой сигнал обратной связи берется из общей для всех трех цепей точки. Это удалось сделать благодаря тому, что дополнительно включили звено с передаточной функцией . Покажем это. В схеме на рис. 5.5.а изображение сигнала на входе звенаравно. Тогда. Помножим Y(p) наи получим, то есть на звенопоступает тот же самый сигнал, что и в схеме на рис. 5.5.а. Таким образом, эквивалентность схем на рис. 5.5.а и на рис. 5.5.б доказана.

Теперь поэтапно получим выражение для передаточной функции системы на рис. 5.5.б. Передаточная функция внутреннего контура на основании с учетомравна=.

Так как две цепи обратных связей имеют общий входной сигнал y(t) и вводятся в одну точку на входе, следовательно они образуют звено передачи, соединенное по параллельной схеме. Передаточная функция этого звена с учетом иравна. Тогда на основании (5.6) получим выражение для передаточной функции системы на рис. 5.5.б:

=, гдеопределяется по приведенному выше выражению.

Используя приведенные формулы ,,и, а также описанные приемы и преобразования, можно получить выражения для передаточных функций систем со сложной конфигурацией схемы и со многими цепями обратных связей.

22. Признак и условие устойчивости замкнутых сау.

Признаком устойчивости системы является следующее: если после воздействия на систему короткого импульса она с течением времени приходит в состояние покоя, то данная система устойчива. Математически это записывается так: .

Системы без обратных связей всегда устойчивы, в этих системах коэффициенты в (5.12) .

Системы с обратными связями не всегда устойчивы. В неустойчивых системах возникают незатухающие колебания, которые нарушают нормальную работу систем и могут даже разрушить их.

Как уже отмечалось в разделе 2, САУ с передаточной функцией вида 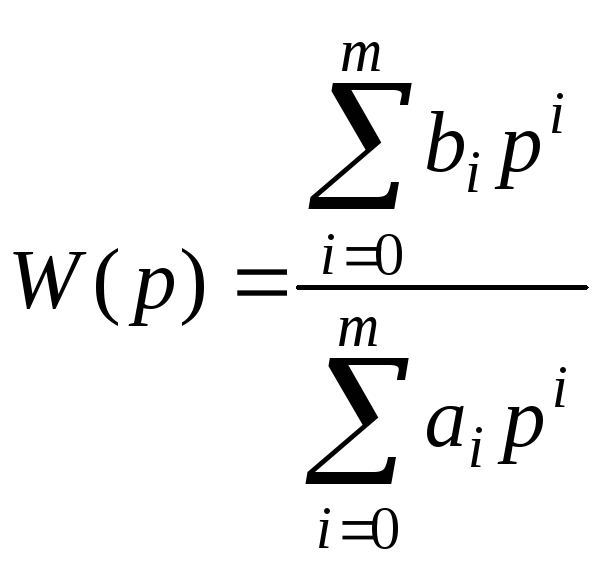описывается дифференциальным уравнением, (5.12) гдесимвол дифференцирования.

После прекращения входного воздействия правая часть уравнения (5.12) равна нулю, и оно превращается в однородное дифференциальное уравнение .

Решение этого уравнения имеет следующий вид: , (5.13)

где - коэффициенты,- полюсы . Полюсы - это корни характеристического уравнения, получаемого приравниванием нулю знаменателя функции W(р).

В общем случае при действительных коэффициентах полюсы являются действительными или комплексно-сопряженными числами

или,. Тогда.

Подставив это выражение в (5.13), получим .

Из этого выражения следует, что необходимым и достаточным условием устойчивости САУ, когда , является условие, т.е. в устойчивых системах действительные части всех корней характеристического уравнения системы должны быть отрицательны.

Это простое на первый взгляд условие может быть проверено на практике только при степени характеристического уравнения . Приобщего аналитического решения характеристических уравнений не найдено. Поэтому придля оценки устойчивости САУ предложено несколько косвенных методов проверки устойчивости САУ без решения характеристического уравнения.