8.10. Приведенное количество тепла. Неравенство Клаузиуса

Коэффициент полезного действия для любой тепловой машины

,

где Q₁ - количество теплоты, отданное нагревателем, Q₂ - отданное холодильнику.

Коэффициент полезного действия обратимой тепловой машины (цикл Карно)

,

где Т₁ – температура нагревателя, Т₂ – температура холодильника.

В случае обратимого процесса между этими величинами должен стоять знак равенства:

(8.9)

В случае необратимого процесса – знак неравенства:

(8.10)

Соотношения (8.9) и (8.10) можно объединить и записать в виде

или .

Умножив полученное выражение на положительную величину , получим

.

Вычитая из левой и правой части , имеем

. (8.11)

В соотношение (8.11) входит как тепло, полученное системой Q₁, так и тепло, отдаваемое ею Q₂. Вместо отдаваемого телу тепла Q₂ введем полученное от этого тела тепло, равное -Q₂. Тогда выражение (8.11) запишется в виде

. (8.12)

Это соотношение носит название неравенства Клаузиуса.

Отношение количества тепла, полученного системой от какого-либо тела, к температуре этого тела называется приведенным количеством тепла. Используя эту терминологию Клаузиуса, выражение (8.12) может быть сформулировано следующим образом: при обратимом цикле Карно сумма приведенных количеств тепла равно нулю, при необратимом цикле – меньше нуля.

Неравенство Клаузиуса может быть обобщено на любой круговой процесс. Любой круговой процесс может быть разбит на весьма большое число элементарных циклов Карно. Каждый из этих элементарных циклов Карно протекает между нагревателем соответствующей температуры T_i, от которого он получает количество тепла Q_i, и холодильником соответствующей температуры T_k, которому он отдает количество тепла Q_k. Для этого элементарного цикла напишем неравенство Клаузиуса:

. (8.13)

Суммируя выражение (8.13), написанное для каждого из элементарных циклов, получим для всего цикла

. (8.14)

Т.е. для всякого кругового процесса сумма приведенных количеств тепла не может быть больше нуля. В случае обратимого протекания процесса можно показать, что сумма (8.14) преобразуется в контурный интеграл

,

где интеграл берется по всему циклу.

8.11. Энтропия. Свойства энтропии. Закон возрастания энтропии в замкнутых системах

Возьмем какой-либо обратимый цикл (рис.8.13) и выделим в нем

два произвольных состояния (1) и (2). Эти состояния делят цикл на две ветви, которые обозна-чены на рис.8.13 и. Сумма приведенных количеств тепла, взятая по всему циклу, равна нулю: .

2   1 Рис.8.13

Для рассматриваемого цикла

. (8.15)

Если изменить направление перехода, то в силу обратимости процесса, каждое слагаемое суммы должно изменить знак. Так, если при направлении процесса от состояния (1) к состоянию (2) система получает от какого-то тела с температурой Т количество тепла Q, то при направлении процесса (2-1) на том же участке система должна отдавать этому же телу с температурой Т такое же количество Q, т.е. получить -Q.

Таким образом,

. (8.16)

Исходя из неравенств (8.15) и (8.16), можно получить следующее соотношение:

.

Отсюда следует, что

,

т.е. сумма приведенных количеств тепла, полученных системой при обратимом переходе от одного состояния (начальное) в другое (конечное), не зависит от пути, по которому совершается переход и, следовательно, зависит только от начального и конечного состояний. Величины, изменения которых при переходе из одного состояния в другие не зависят от пути перехода, называются функциями состояния. Независимость суммы 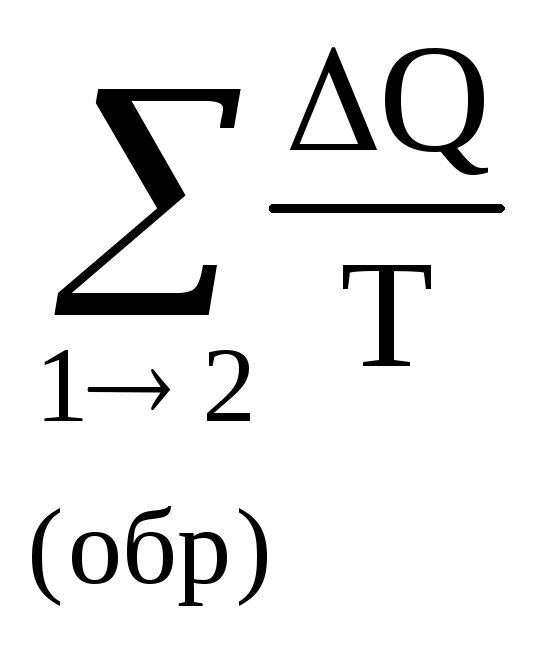от пути, по которому совершается обратимый переход из состояния (1) в состояние (2) дает основание утверждать, что при обратимом процессепредставляет собой приращение некоторой функции состояния. Эта функция была названа энтропией и обозначается буквойS.

Таким образом,

.

Согласно этому равенству, приращение энтропии равно элементарному количеству тепла, получаемому обратимо системой извне, отнесенному к температуре, при которой это тепло получается. Поскольку энтропия – функция состояния, сумма приращений энтропии должна быть равна разности значений энтропии в конечном и начальном состояниях:

. (8.17)

Более того, суммы должны быть заменены интегралом

.

Итак, при обратимом процессе сумма приведенных количеств тепла равна приращению энтропии.

Выясним, в каком соотношении находятся сумма приведенных количеств тепла и приращение энтропии при необратимом процессе. Для этого рассмотрим цикл, состоящий из обратимой и необратимой ветвей (рис.8.14).

Поскольку в целом цикл необратим, сумма приведенных количеств тепла, взятая по всему циклу, должна быть меньше нуля: .

2 Необр. Обр. 1 Рис.8.14

Разобьем эту сумму на две части, отнесенные к разным ветвям:

. (8.18)

Вторая из этих сумм равна разности энтропий в состояниях 1 и 2 (8.17). Поэтому соотношение (8.18) можно записать в виде

или . (8.19)

Объединяя вместе (8.17) и (8.19), получим

,

т.е. приращение энтропии больше или равна сумме приведенных количеств тепла.

Знак равенства соответствует любому обратимому переходу 12. Знак неравенства – любому необратимому переходу из состояния (1) в состояние (2). Температура Т означает температуру того тела, от которого система получает тепло Q.

При обратимом процессе эта температура совпадает с температурой системы. Если система изолирована, т.е. не обменивается теплом, то все Q будут равны нулю, вследствие чего

S₂ – S₁  0

или, соответственно,

S  0.

Таким образом, энтропия изолированной системы может только возрастать (если в системе протекает необратимый процесс), либо оставаться постоянной (если в системе протекает обратимый процесс). Убывать энтропия изолированной системы не может.

Если система обменивается теплом с внешней средой, ее энтропия может вести себя любым образом. В частности, если система отдает тепло внешним телам, энтропия системы уменьшается. Если неизолированная система совершает цикл, то ее энтропия возрастая на одних участках цикла и убывая на других, в конце цикла принимает первоначальное значение.

Энтропия – аддитивная величина. Это означает, что энтропия системы равна сумме энтропий отдельных ее частей.