
- •Введение
- •Физические основы механики
- •1. Кинематика поступательного и вращательного движения
- •1.1. Система отсчета. Путь. Вектор перемещения
- •1.2. Скорость. Ускорение при криволинейном движении
- •1.3. Нормальное, тангенциальное и полное ускорения
- •1.4. Движение точки по окружности. Угловая скорость. Угловое ускорение
- •2. Динамика поступательного движения
- •2.1. Законы Ньютона
- •2.2. Силы в механике
- •2.2.1. Сила тяжести
- •2.2.2. Упругие силы
- •2.2.3. Сила трения
- •2.3. Внешние и внутренние силы. Закон сохранения импульса
- •3. Работа и энергия
- •3.2. Кинетическая энергия механической системы и её связь с работой
- •3.3. Потенциальная энергия материальной точки во внешнем силовом поле и ее связь с силой, действующей на материальную точку
- •3.4. Потенциальная энергия системы взаимодействия. Связь кинетической энергии системы с работой внутренних и внешних сил
- •3.5. Закон сохранения механической энергии. Закон сохранения и превращения энергии как проявление неуничтожимости материи и ее движения
- •3.6. Удар абсолютно упругих и неупругих тел
- •4. Динамика вращательного движения
- •4.1. Момент силы и момент импульса
- •4.2. Уравнение моментов
- •4.3. Движение центра тяжести твердого тела
- •4.4. Момент инерции тела относительно оси вращения
- •4.5. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси. Закон сохранения момента импульса
- •4.6. Кинетическая энергия твердого тела. Работа внешних сил при вращении твердого тела
- •4.7. Кинетическая энергия при плоском движении твердого тела
- •5. Элементы специальной теории относительности
- •5.1. Преобразования Галилея. Механический принцип относительности
- •5.2. Постулаты специальной теории относительности. Преобразования Лоренца
- •5.3. Следствия из преобразований Лоренца
- •5.3.1. Одновременность событий в разных системах отсчета
- •5.3.2. Длина тел в разных системах отсчета
- •5.3.3. Длительность событий в разных системах отсчета
- •5.4. Пространственно-временной интервал
- •5.5. Релятивистская кинематика. Релятивистский закон сложения скоростей
- •5.6. Релятивистская динамика
- •6. Механические колебания и волны
- •6.1. Понятия о колебательных процессах. Гармонические колебания. Амплитуда. Частота. Фаза колебаний
- •6.2. Свободные гармонические колебания
- •6.2.1. Математический маятник
- •6.2.2. Пружинный маятник
- •6.2.3. Физический маятник
- •6.2.4. Скорость и ускорение точки, колеблющейся по гармоническому закону
- •6.2.5. Энергия гармонических колебаний
- •6.3. Сложение колебаний
- •6.3.1. Сложение колебаний одного направления и одинаковой частоты
- •6.3.2. Сложение двух гармонических колебаний одного направления, но разного периода
- •6.3.3. Сложение взаимно перпендикулярных колебаний
- •6.4. Затухающие колебания
- •6.5. Вынужденные колебания. Резонанс
- •6.6. Волновые процессы
- •6.6.1. Плоская синусоидальная волна. Фазовая скорость. Длина волны. Групповая скорость
- •6.6.2. Скорость распространения волн в упругой среде
- •6.6.3. Поток энергии в волновых процессах
- •6.6.4. Принцип Гюйгенса-Френеля. Интерференция волн
- •6.6.5. Отражение волн. Стоячие волны
- •7. Молекулярно-кинетическая теория
- •7.1. Статистический метод исследования. Термодинамический метод исследования. Термодинамические параметры. Равновесное состояние и процессы их изображения на термодинамических диаграммах
- •7.2. Основное уравнение молекулярно-кинетической теории газов
- •7.3. Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование абсолютной температуры. Связь основного уравнения мкт с уравнением Менделеева-Клайперона
- •7.4. Средняя скорость молекул. Поток молекул
- •7.5. Распределение молекул по скоростям. Закон Максвелла
- •7.6. Барометрическая формула.
- •7.7. Больцмановское распределение частиц в потенциальном поле. Закон Максвелла-Больцмана
- •7.8. Экспериментальный метод определения числа Авогадро
- •7.9. Эффективный диаметр молекулы. Число столкновений и средняя длина свободного пробега молекулы
- •7.10. Явления переноса в газах
- •7.10.1. Вязкость газов (внутреннее трение)
- •7.10.2. Закон Стокса
- •7.10.3. Теплопроводность газов
- •7.10.4. Диффузия газов
- •8. Термодинамика
- •8.1. Внутренняя энергия системы. Работа. Количество теплоты. Первое начало термодинамики
- •8.2. Степени свободы молекул. Распределение энергии по степеням свободы
- •8.3. Молекулярно-кинетическая теория теплоемкости газа
- •8.4.1. Изохорный процесс
- •8.4.2. Изотермический процесс
- •8.4.3. Изобарный процесс
- •8.5. Адиабатический процесс
- •8.7. Цикл Карно
- •8.8. Принцип действия тепловой и холодильной машин
- •8.9. Второе начало термодинамики
- •8.10. Приведенное количество тепла. Неравенство Клаузиуса
- •8.12. Статистический смысл второго начала термодинамики. Связь энтропии с термодинамической вероятностью
- •9. Агрегатные состояния и фазовый переход
- •9.1. Реальные газы. Уравнение Ван-дер-Ваальса
- •9.2. Экспериментальные изотермы. Критические состояния
- •9.3. Внутренняя энергия реального газа. Эффект
- •Библиографический список
- •Оглавление
6.4. Затухающие колебания
Всякое реальное колебание происходит с постепенным расходованием энергии движения на работу против сил трения. При этом амплитуда и скорость колебательного движения убывают. Полная сила, действующая на колеблющуюся точку, будет тогда суммой квазиупругой силы и силы трения:
F = Fупр+Fтр
При малых скоростях движения сопротивление обычно пропорционально первой степени скорости и направлено противоположно ей:
Fтр= r,
где r - коэффициент трения, зависящий от свойств среды, формы и размеров движущегося тела.
Уравнение движения тела в этом случае имеет вид
![]() Fупр+Fтр;
Fупр+Fтр;
![]() .
(6.27)
.
(6.27)
Введем обозначения
![]() ;
;
![]()
и перепишем уравнение (6.27):
![]() ,
(6.28)
,
(6.28)
где 0 - собственная частота колебания системы.
Будем искать решение уравнения (6.28) в виде
![]() ,
(6.29)
,
(6.29)
где A(t) - некоторая функция времени.
Найдем первую производную от уравнения (6.29):
![]() (6.30)
(6.30)
и вторую производную:
![]() .
(6.31)
.
(6.31)
Подставляя уравнения (6.29), (6.30), (6.31) в (6.28), получим
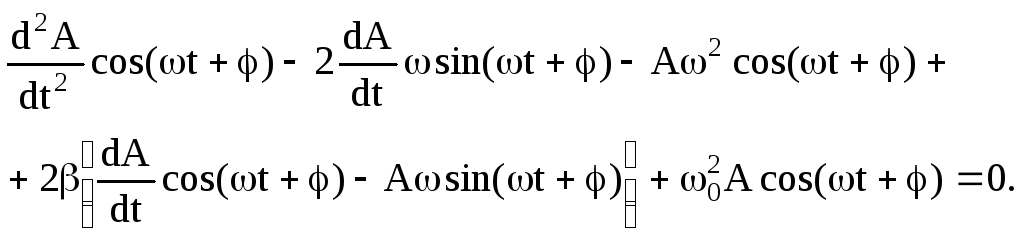
Сгруппируем члены при cos(t+) и sin(t+):
![]() .
.
Для того, чтобы данное уравнение удовлетворялось при любых значениях t, необходимо равенство нулю коэффициентов при cos(t+) и sin(t+).
Таким образом, мы приходим к двум уравнениям:
![]() ;
(6.32)
;
(6.32)
![]() .
(6.33)
.
(6.33)
Из уравнения (6.32)
получим
![]() .
.
Проинтегрируем выражение
 ;
;
![]() .
.
Производя потенцирование найденного соотношения, получим выражение для амплитуды колебаний:
A=A0e-t.
Легко увидеть, что
![]() ,
а
,
а![]() .
.
Подстановка этих значений в уравнение (6.33) приводит к соотношению
![]() ,
,
из которого после сокращения А получаем
![]() ,
,
![]() .
.
При
![]() частота затухающих колебаний
будет величиной вещественной, и решением
дифференциального уравнения (6.28) является
функция вида
частота затухающих колебаний
будет величиной вещественной, и решением
дифференциального уравнения (6.28) является
функция вида
![]() .
(6.34)
.
(6.34)
График этой функции дан на рис.6.15.
Сравнивая полученное решение (6.34) решением уравнений гармонических колебаний
x=Acos(t+),
следует заметить, что последние отличаются от чисто гармонических колебаний тел, что амплитуда колебания
![]()
является убывающей функцией времени.
|
На графике (рис.6.15) она показана пунктирной линией.
Величина
|
A0
O t
-A0
Рис.6.15
|
![]() ;
;
![]()
или
 .
.
С увеличением трения период колебаний возрастает, а при =0 период становится бесконечным. При дальнейшем увеличении период становится мнимым, а движение точки или тела – апериодическим (рис.6.16). Вычислим отношение амплитуд, отстоящих друг от друга во времени на один период:
 .
.
|
O t Рис.6.16 |
Отношение амплитуд зату-хающих колебаний, отстоящих друг от друга на интервал времени, равный периоду, постоянно во все время колебания. Натуральный лога-рифм этого отношения называется логарифмическим декрементом затухания:
|
Логарифмический декремент затухания характеризующий быстроту убывания амплитуды, прямо пропорционален величине коэффициента сопротивления и обратно пропорционален массе системы. Таким образом, из-за наличия сил трения собственные колебания точки или тела будут затухающими.

 x
x x
x