
- •Введение
- •Физические основы механики
- •1. Кинематика поступательного и вращательного движения
- •1.1. Система отсчета. Путь. Вектор перемещения
- •1.2. Скорость. Ускорение при криволинейном движении
- •1.3. Нормальное, тангенциальное и полное ускорения
- •1.4. Движение точки по окружности. Угловая скорость. Угловое ускорение
- •2. Динамика поступательного движения
- •2.1. Законы Ньютона
- •2.2. Силы в механике
- •2.2.1. Сила тяжести
- •2.2.2. Упругие силы
- •2.2.3. Сила трения
- •2.3. Внешние и внутренние силы. Закон сохранения импульса
- •3. Работа и энергия
- •3.2. Кинетическая энергия механической системы и её связь с работой
- •3.3. Потенциальная энергия материальной точки во внешнем силовом поле и ее связь с силой, действующей на материальную точку
- •3.4. Потенциальная энергия системы взаимодействия. Связь кинетической энергии системы с работой внутренних и внешних сил
- •3.5. Закон сохранения механической энергии. Закон сохранения и превращения энергии как проявление неуничтожимости материи и ее движения
- •3.6. Удар абсолютно упругих и неупругих тел
- •4. Динамика вращательного движения
- •4.1. Момент силы и момент импульса
- •4.2. Уравнение моментов
- •4.3. Движение центра тяжести твердого тела
- •4.4. Момент инерции тела относительно оси вращения
- •4.5. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси. Закон сохранения момента импульса
- •4.6. Кинетическая энергия твердого тела. Работа внешних сил при вращении твердого тела
- •4.7. Кинетическая энергия при плоском движении твердого тела
- •5. Элементы специальной теории относительности
- •5.1. Преобразования Галилея. Механический принцип относительности
- •5.2. Постулаты специальной теории относительности. Преобразования Лоренца
- •5.3. Следствия из преобразований Лоренца
- •5.3.1. Одновременность событий в разных системах отсчета
- •5.3.2. Длина тел в разных системах отсчета
- •5.3.3. Длительность событий в разных системах отсчета
- •5.4. Пространственно-временной интервал
- •5.5. Релятивистская кинематика. Релятивистский закон сложения скоростей
- •5.6. Релятивистская динамика
- •6. Механические колебания и волны
- •6.1. Понятия о колебательных процессах. Гармонические колебания. Амплитуда. Частота. Фаза колебаний
- •6.2. Свободные гармонические колебания
- •6.2.1. Математический маятник
- •6.2.2. Пружинный маятник
- •6.2.3. Физический маятник
- •6.2.4. Скорость и ускорение точки, колеблющейся по гармоническому закону
- •6.2.5. Энергия гармонических колебаний
- •6.3. Сложение колебаний
- •6.3.1. Сложение колебаний одного направления и одинаковой частоты
- •6.3.2. Сложение двух гармонических колебаний одного направления, но разного периода
- •6.3.3. Сложение взаимно перпендикулярных колебаний
- •6.4. Затухающие колебания
- •6.5. Вынужденные колебания. Резонанс
- •6.6. Волновые процессы
- •6.6.1. Плоская синусоидальная волна. Фазовая скорость. Длина волны. Групповая скорость
- •6.6.2. Скорость распространения волн в упругой среде
- •6.6.3. Поток энергии в волновых процессах
- •6.6.4. Принцип Гюйгенса-Френеля. Интерференция волн
- •6.6.5. Отражение волн. Стоячие волны
- •7. Молекулярно-кинетическая теория
- •7.1. Статистический метод исследования. Термодинамический метод исследования. Термодинамические параметры. Равновесное состояние и процессы их изображения на термодинамических диаграммах
- •7.2. Основное уравнение молекулярно-кинетической теории газов
- •7.3. Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование абсолютной температуры. Связь основного уравнения мкт с уравнением Менделеева-Клайперона
- •7.4. Средняя скорость молекул. Поток молекул
- •7.5. Распределение молекул по скоростям. Закон Максвелла
- •7.6. Барометрическая формула.
- •7.7. Больцмановское распределение частиц в потенциальном поле. Закон Максвелла-Больцмана
- •7.8. Экспериментальный метод определения числа Авогадро
- •7.9. Эффективный диаметр молекулы. Число столкновений и средняя длина свободного пробега молекулы
- •7.10. Явления переноса в газах
- •7.10.1. Вязкость газов (внутреннее трение)
- •7.10.2. Закон Стокса
- •7.10.3. Теплопроводность газов
- •7.10.4. Диффузия газов
- •8. Термодинамика
- •8.1. Внутренняя энергия системы. Работа. Количество теплоты. Первое начало термодинамики
- •8.2. Степени свободы молекул. Распределение энергии по степеням свободы
- •8.3. Молекулярно-кинетическая теория теплоемкости газа
- •8.4.1. Изохорный процесс
- •8.4.2. Изотермический процесс
- •8.4.3. Изобарный процесс
- •8.5. Адиабатический процесс
- •8.7. Цикл Карно
- •8.8. Принцип действия тепловой и холодильной машин
- •8.9. Второе начало термодинамики
- •8.10. Приведенное количество тепла. Неравенство Клаузиуса
- •8.12. Статистический смысл второго начала термодинамики. Связь энтропии с термодинамической вероятностью
- •9. Агрегатные состояния и фазовый переход
- •9.1. Реальные газы. Уравнение Ван-дер-Ваальса
- •9.2. Экспериментальные изотермы. Критические состояния
- •9.3. Внутренняя энергия реального газа. Эффект
- •Библиографический список
- •Оглавление
4.3. Движение центра тяжести твердого тела
Абсолютно твердым телом называется тело, расстояние между двумя точками которого во время движения остается неизменным. Разобьем мысленно такое тело на бесконечно малые элементы, которые малы по сравнению с расстоянием до оси вращения. Каждый такой элемент тела мы можем рассматривать как материальную точку. Таким образом, мы сведем задачу о движении твердого тела к задаче о движении большого числа отдельных материальных точек.
Обозначим массу i–элемента через mi, его скорость через i. Запишем уравнение второго закона Ньютона для каждого из элементов:
![]() ,
,
где
![]() - сумма внутренних сил,
- сумма внутренних сил,![]() - внешняя сила, действующая на элемент
массы.
- внешняя сила, действующая на элемент
массы.
Складывая для всех элементов тела, получим
![]() ,
(4.4)
,
(4.4)
так как по третьему
закону Ньютона сумма всех внутренних
сил, действующих на отдельные элементы
тела
![]() .
.
Согласно (4.4) так же, как и для всякой системы материальных точек, производная по времени от общего импульса тела равна сумме всех внешних сил, действующих на тело.
Координаты центра масс твердого тела определяются следующим образом:
 ;
;
 ;
;
 ,
,
где
![]() - координаты элемента массыmi(рис.4.4).
- координаты элемента массыmi(рис.4.4).
Продифференцируем по времени эти выражения:
|
mi zi x
yi xi y Рис.4.4
|
|
Справа стоят
компоненты общего импульса системы по
трем осям координат. Слева – масса тела,
умноженная на соответствую-щие компоненты
скорости центра масс
![]() .
Складывая почленно, получим
.
Складывая почленно, получим
![]() ,
(4.5)
,
(4.5)
где
![]() - вектор скорости центра масс,m
- масса всего тела.
- вектор скорости центра масс,m
- масса всего тела.
Из выражения (4.5) следует, что твердое тело обладает таким же импульсом, каким обладала бы материальная точка массы, равной массе тела и движущаяся, как движется центр масс тела.
Подставляя (4.5) в уравнение (4.1), получим
![]() .
(4.6)
.
(4.6)
Поскольку масса тела есть величина постоянная, её можно вынести за знак дифференциала и уравнение движения центра масс твердого тела (4.6) примет следующий вид:
![]() .
(4.7)
.
(4.7)
Центр масс твердого тела движется так, как двигалась бы материальная точка той же массы под действием всех внешних сил, которые действуют на данное тело.
Умножим векторно
обе части уравнения (4.7) на
![]() :
:
![]() .
.
Правая часть этого уравнения есть момент сил, действующих на абсолютно твердое тело:
![]() .
.
Левая часть есть производная от момента импульса абсолютно твердого тела относительно выбранной оси
![]() .
.
Следовательно, и для абсолютно твердого тела уравнение моментов имеет следующий вид:
![]() .
(4.8)
.
(4.8)
4.4. Момент инерции тела относительно оси вращения
Моментом инерции тела относительно оси вращения называется сумма произведений элементарных масс на квадрат расстояния от оси вращения:
![]() .
.
Для тела с неравномерно распределенной массой элементарная масса mi
![]() ,
,
где i- плотность в данной точке,Vi- элементарный объем. Поэтому момент инерции тела будет равен
![]() .
.
Если =сonst, то
![]() .
.
Переходя к пределу получим, что
![]() .
.
|
z
dr b
Рис.4.5 |
Найдем момент инерции однородного диска относительно оси, перпендикулярной к плос-кости диска и проходящей через его центр (рис.4.5). Разобьем диск на кольцевые слои толщиной dr. Объем такого слоя равен V=b2rdr, где b - толщина диска, r – радиус кольцевого слоя. |
Поскольку диск однороден, то =сonst и
![]() ;
;
![]() ,
,
где R- радиус диска.
Произведение
![]() ,
поэтому момент инерции диска относительно
оси, перпендикулярной к плоскости и
проходящей через его центр будет равен
,
поэтому момент инерции диска относительно
оси, перпендикулярной к плоскости и
проходящей через его центр будет равен
![]() .
.
Для нахождения момента инерции диска относительно оси, не проходящей через его центр, воспользуемся теоремой Штейнера.
|
Момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, парал-лельной данной и проходящей через центр инерции тела и произведения массы тела на квадрат расстояния между осями (рис.4.6):
|
O O
O O Рис.4.6
|
В соответствии с этой теоремой, момент инерции диска относительно оси ООравен
![]() .
.
Приведем моменты инерции тел различной геометрической формы.
1. Длинный стержень,
толщина которого значительно меньше
длины
![]() .
Момент инерции относительно оси,
перпендикулярной к стержню и проходящий
через его середину
.
Момент инерции относительно оси,
перпендикулярной к стержню и проходящий
через его середину![]() (рис.4.7,а).
Относительно оси ОО(рис.4.7,б),
согласно теореме Штейнера
(рис.4.7,а).
Относительно оси ОО(рис.4.7,б),
согласно теореме Штейнера
![]() ,
,
т.е.
![]() .
.
2. Момент инерции
шара относительно оси, проходящей через
его центр (рис.4.8,а)![]() .
Относительно оси ОО(рис.4.8,б)
.
Относительно оси ОО(рис.4.8,б)![]() .
.
|
О а)
О
О О б) Рис.4.7 |
R
O О О а) б)
Рис.4.8 |
3. Момент инерции
полого цилиндра относительно оси,
проходящей через его центр
![]() .
.
4. Момент инерции
полого цилиндра (обруча) с внутренним
радиусом R1и внешнимR2относительно оси
цилиндра![]() для тонкостенного полого цилиндраR1R2=Rи I=mR2.
для тонкостенного полого цилиндраR1R2=Rи I=mR2.

 z
z

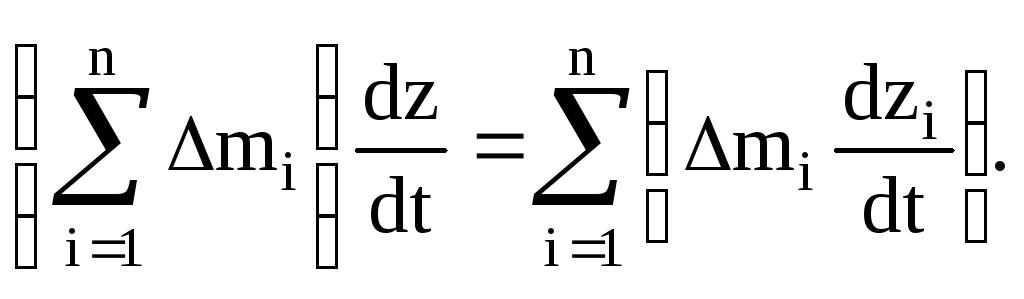


 О
О OО О
OО О