
- •1. Основы микросхемотехники ИС
- •1.1. Основные термины и определения
- •1.2. Этапы и направления развития ИС
- •1.3. Классификация ИС
- •1.3.4. Классификация по степени интеграции
- •1.4. Последовательность разработки ИС
- •2. Основы цифровой техники
- •2.3. Основные логические операции
- •2.4. Формы представления логической функции
- •2.5. Структурное проектирование цифровых схем комбинационного типа
- •3. Основные параметры и характеристики ЦИС
- •3.1. Основные параметры ЦИС
- •3.2. Характеристики ЦИС
- •3.3. Определение измеряемых параметров по характеристикам
- •4.1. Формирование биполярных транзисторов
- •4.3. Эквивалентная модель интегрального n–p–n биполярного транзистора
- •4.4. Режимы работы биполярного транзистора
- •4.6. Статические ВАХ транзистора
- •5. Диоды в интегральных схемах
- •5.1. Модель идеального диода
- •5.2. Эквивалентная схема интегрального диода
- •5.3. Аппроксимации ВАХ диода
- •5.4. Варианты реализации интегральных диодов
- •6. Пассивные элементы ИС
- •6.1. Основные параметры резисторов
- •6.2. Реализация интегральных резисторов
- •6.4. Реализация интегральных конденсаторов
- •7. Элементная база статических ЦИС на биполярных транзисторах
- •7.1. Резисторно-транзисторная логика (РТЛ)
- •7.1.1. Характеристики РТЛ
- •7.2. Эмиттерно-связанная логика (ЭСЛ)
- •7.2.1. Принцип работы
- •7.2.2. Входная характеристика
- •7.2.3. Передаточная характеристика
- •7.2.4. Выходная характеристика
- •7.2.6. Многоярусные ЭСЛ (МяЭСЛ)
- •7.3. Диодно-транзисторная логика
- •7.3.1. Расчет передаточной и входной характеристик
- •7.3.2. Выходная характеристика
- •7.3.3. Влияние нагрузки на логические уровни
- •7.4. Транзисторно-транзисторная логика
- •7.4.1. ТТЛ-элемент с простым инвертором
- •7.4.2. Передаточная характеристика
- •7.4.3. Входная характеристика
- •7.4.4. Выходная характеристика
- •7.4.6. Основные параметры
- •7.4.7. Многоэмиттерный транзистор
- •7.4.8. ТТЛ-элемент со сложным выходным каскадом
- •7.4.9. Модификация логического элемента
- •7.5. Интегральная инжекционная логика
- •7.5.2. Реализация логических функций
- •8. Полевые транзисторы
- •8.1. Типы полевых транзисторов
- •8.2. Определение физических параметров
- •8.3. модель полевого транзистора
- •8.4. Режимы работы и уравнения ВАХ полевого транзистора
- •9. Элементная база на полевых транзисторах
- •9.2. Передаточная характеристика и параметры инвертора с линейной нагрузкой
- •9.3. Передаточная характеристика и параметры инвертора с нелинейной нагрузкой
- •9.4. Передаточная характеристика и параметры инвертора с квазилинейной нагрузкой
- •9.5. Передаточная характеристика и параметры инвертора с токостабилизирующей нагрузкой
- •9.6. Передаточная характеристика и параметры комплементарного инвертора
- •9.8. Логические элементы на МОП-транзисторах
- •9.9. Определение эквивалентной крутизны группы переключающих транзисторов
- •9.11. Влияние параметров транзисторов на характеристики логического элемента
- •9.12. Сопряжение ТТЛ- и КМОП-схем
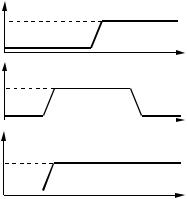
2.5. Структурное проектирование цифровых схем комбинационного типа
Комбинационными называются функциональные блоки, логическое состояние выходов которых зависит только от комбинации логических сигналов на входах в данный момент времени. Изготавливаются в виде МИС (И-НЕ, ИЛИ-НЕ и др.), либо СИС,
UA |
|
U1 |
|
U0 |
t |
UB |
|
U1 |
|
U0 |
t |
UF |
|
U1 |
|
U0 
t
Рис.2.3. Графическая форма представления логической функции ИЛИ
либо входят в состав БИС и СБИС. Для проектирования используется макроэлементный метод (IP блоки), включающий разработку структуры, схемы и топологии макроэлементов (функциональных узлов), а затем с помощью этих макроэлементов компонуется БИС.
Рассмотрим методику структурного проектирования комбинационного блока.
Исходными данными для проектирования комбинационного блока являются:
25

1)функциональное описание в виде таблицы истинности или алгебраического выражения;
2)требования к основным электрическим параметрам.
Задача структурного проектирования - получить наиболее простое (минимизированное) логическое выражение реализуемой функции и построить соответствующую структурную схему на заданной или выбранной элементной базе.
Минимизация логической функции заключается в упрощении ее алгебраического выражения. Чем меньше элементов требуется для ее выполнения, тем лучшие показатели по быстродействию, потребляемой мощности и занимаемой площади на кристалле будет иметь микросхема.
Минимизацию, т.е. упрощение логической функции, можно выполнить:
·либо с помощью преобразований алгебры логики
F= ABC + ABC = BC(A + A) = BC ;
·либо с помощью карты Карно.
Карта Карно используется для минимизации логической функции с небольшим количеством переменных (k £ 6). Для функции с большим количеством переменных декомпозицией можно выделить более простые ее составляющие, которые минимизируются с помощью карты Карно.
Структурное проектирование осуществляется поэтапно.
1. Функция приводится к СДНФ или СКНФ с помощью раскрытия скобок и преобразований по закону дуальности. Очень часто используется правило двойной инверсии:
F= (A + BC)(C + D) = (A + BC) + (C + D) = A × BC + C D =
=A × (B + C) + C D = A × (B + C) + C D = A B + AC + C D;
F= A(C + D) + BC = AC + AD + BC = AC × AD × BC =
=(A + C)(A + D)(B + C) = (A + C)(A + D)(B + C).
2.Заполняется карта Карно для полученной функции.
26
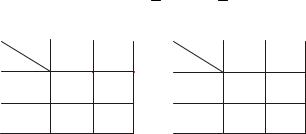
Если логическая функция имеет СДНФ, то заполняется карта Карно по 1 (рис.2.4,а) (так как функция равна 1, если хотя бы одно слагаемое равно 1).
|
|
|
|
|
|
|
|
|
F = AB + |
A |
|
B |
. |
|
|
|
|
|
|
ìA = 1 |
|
|
|
|
|
|
|
||
1) AB =1 |
í |
|
|
|
|
|
|
|
|
|
||||
îB = 1 , |
|
|
|
|
|
|
||||||||
|
|
|
|
|
ì |
|
|
ìA = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ïA =1 |
|
|
|
|
|
||||
|
|
|
|
|
í |
|
|
Þ í |
B = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
A B =1 |
ï |
|
|
î |
|
|
|
|
|
||||
2) |
îB =1 |
|
. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При остальных значениях входных логических переменных функция принимает значение 0.
Если логическая функция имеет СКНФ, то заполняется карта Карно по 0 (рис.2.4,б) (так как функция равна 0, если хотя бы один сомножитель равен 0).
F = (A + B)(A + B).
A
B 0 1
0 12 0
1 0 11
а
A
B 0 1
0 1 01
1 02 1
б
Рис.2.4. Пример заполнения карты Карно для функции XOR, представленной СДНФ (а) и СКНФ (б)
|
|
|
|
|
ì |
|
|
= 0 |
ìA =1 |
|
|
|
|
|
A |
||||
|
|
|
|
|
í |
|
|
|
Þ í |
|
|
+ B = 0 |
îB = 0 |
îB = 0 , |
|||||
1) |
A |
||||||||
|
|
|
|
|
ìA = 0 |
ìA = 0 |
|||
|
|
|
|
|
í |
|
|
|
Þ í |
|
|
|
|
|
|
|
|
||
2) |
A + |
B |
= 0 |
îB = 0 |
îB =1. |
||||
При остальных значениях входных логических переменных функция принимает значение 1.
27

3. Минимизацию функции можно проводить либо по 1, либо по 0. Как правило, минимизация, т.е. объединение соседних состояний, проводится в соответствии с элементным базисом. Проводится объединение соседних 2, 4, 8, 16 (2n) состояний. Объединяться могут клетки по строкам либо по столбцам, либо по квадратам. В результате объединения по правилу склеивания
( ABC + ABC = BC ) записываются те переменные, которые не изменялись при переходе из состояния в состояние. Чем крупнее объединение, тем меньше переменных остается в алгебраическом выражении функции. Одно состояние может войти в несколько разных объединений.
4. После минимизации функция считывается с карты Карно. В алгебраическом выражении функции будет столько слагаемых или сомножителей, сколько объединений было сделано. Например, при считывании по 1 записывается сумма минтермов в СДНФ
F = |
A |
|
C |
+ |
A |
|
B |
+ |
C |
|
D |
|
(рис.2.5,а); при считывании по 0 записыва- |
ется произведение |
макстермов переменных в СКНФ |
||||||||||||
F= (B + C)(A + C)(A + D) (рис.2.5,б).
5.Затем алгебраическое выражение функции преобразовывается к требуемому элементному базису с помощью правила двойной
AB |
00 |
|
01 |
|
10 |
|
|
AB 00 |
|
01 |
|
|
11 |
|
|
|
|
|
10 |
|
|||||||||
|
11 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
CD |
|
|
|
|
|
|
|
|
|
|
|
|
CD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00 |
|
1 |
|
|
|
1 |
1 |
1 |
|
3 |
00 |
|
|
0 |
|
|
|
0 |
|
3 |
|
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
01 |
|
|
|
|
1 |
|
|
|
2 |
|
|
||||||
01 |
|
1 |
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
1 |
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
1 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
0 |
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рис.2.5. Пример минимизации и считывания логической функции, представленной СДНФ (а) и СКНФ (б)
28
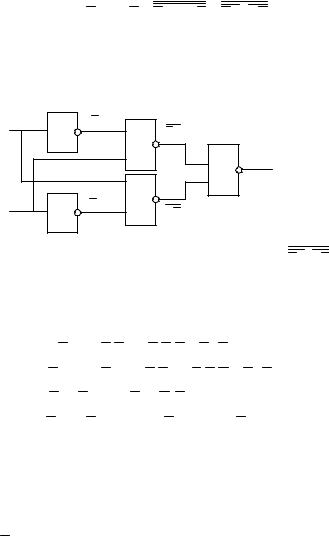
инверсии и теоремы де-Моргана. Например, для реализации XOR на логической функции И-НЕ получим
F = AB + AB = AB + AB = AB × AB.
6. Далее собирается комбинационная схема из логических элементов И-НЕ, НЕ (рис.2.6).
2.6.Примеры преобразований логических функций
1.Преобразование логической функции, представленной в
A |
1 |
A |
& |
AB |
|
|
|
|
|
|
|
|
|
|
|
& |
F |
|
|
|
|
|
|
|
1 |
|
& |
|
|
B |
B |
|
AB |
|
|
|
|
|
|
|
Рис.2.6. Структурная схема логической функции F = AB × AB
алгебраической форме, осуществляется с помощью булевой алгебры.
Например:
F= ABC + ABC + A BC + A B C + ABC =
=(ABC + ABC) + (ABC + A BC + A B C + ABC) =
=BC(A + A) + A[C(B + B) + C(B + B)]=
=BC ×1+ A(C + C) ×1 = BC + A ×1 = BC + A .
Получили минимизированную СДНФ функции.
2. Переход от алгебраической формы представления к табличной выполняется путем последовательной подстановки в данное ал-
гебраическое выражение всех q возможных наборов входных логических переменных и определения fi . У СДНФ функции F = BC + A количество входных логических переменных k = 3 (A, B,C) , поэтому количество возможных наборов входных ло-
29

гических переменных l = 2k = 23 = 8 . Следовательно, таблица истинности рисуется на три переменные с восемью наборами и заполняется последовательным перебором всех состояний
(табл.2.3).
Таблица 2.3
Заполнение таблицы истинности для логической функции F = BC + A
A |
B |
C |
F |
|||||||
0 |
0 |
0 |
F = 0×0 + |
|
|
|
= 0 +1 =1 |
|||
0 |
||||||||||
0 |
0 |
1 |
F = 0 ×1 + |
|
|
|
= 0 + 1 =1 |
|||
0 |
||||||||||
0 |
1 |
0 |
F =1× 0 + |
|
|
|
|
= 0 + 1 =1 |
||
0 |
||||||||||
0 |
1 |
1 |
F =1×1+ |
|
|
|
|
=1+1 =1 |
||
0 |
||||||||||
1 |
0 |
0 |
F = 0×0 +1 = 0 + 0 = 0 |
|||||||
1 |
0 |
1 |
F = 0×1+1 = 0 + 0 = 0 |
|||||||
1 |
1 |
0 |
F =1×0 +1 = 0 + 0 = 0 |
|||||||
1 |
1 |
1 |
F =1×1+1 =1+ 0 =1 |
|||||||
Наиболее быстрый способ составления таблицы истинности заключается в заполнении состояний, при которых СДНФ функция принимает значение 1.
F = BС + |
A |
|
BC = 1 |
|
|
|
|||
ìB = 1 |
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
íC = 1 |
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
îA = " - принимает любое значение (0,1) |
|
||||||||
|
|
ìA = 0 |
|
|
|
|
|
||
|
|
ï |
|
|
|
ìB = 0 |
ìB = 0 |
ìB = 1 |
ìB = 1 |
|
|
íB = " |
|
||||||
|
|
ï |
|
|
|
í |
í |
í |
í |
A = 1 |
îC |
= ", т.е. |
C = 0 |
C = 1 |
C = 0 |
C = 1 |
|||
|
|
|
|
î |
î |
î |
î |
||
Рассмотрим функцию F = BC + СD , у которой количество входных логических переменных k = 3 (B, C, D), т.е. количество воз-
30

можных наборов входных логических переменных равно l = 2k = 23 = 8 . Приведем функцию к СКНФ:
F = BC + СD = BC × CD = (B + C)(C + D).
Теперь можем заполнить таблицу истинности на три переменные с восемью наборами (табл.2.4).
Таблица 2.4
Таблица истинности для функции F = (B + C )(C + D)
B |
C |
D |
F |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
Поскольку функция представлена в СКНФ, то найдем те состояния входных переменных, при которых F = 0:
F = (B + С)(C + D)
|
|
|
|
|
ì |
|
= 0 |
||
|
|
|
|
|
B |
||||
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
íC = 0 |
||||
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
ïD = " |
||||
B + C = 0 |
|||||||||
î |
|
|
|
||||||
|
|
|
|
|
ìC = 0 |
||||
|
|
|
|
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
íD = 0 |
||||
|
|
|
|
|
ïB = " |
||||
C + D = 0 |
|||||||||
î |
|
|
|
||||||
ìB =1
ïíC =1
ïîD = ",т.е. D = 0, D =1
ìC = 0
ïíD = 1
ïîB = ", т.е. B = 0, B = 1
3. Считывание алгебраического выражения функции с таблицы истинности выполняется следующим образом. Если необходимо получить СДНФ функции, то из таблицы истинности считывают-
31

ся те состояния входных логических переменных, при которых функция принимает значение 1 (табл.2.5):
FСДНФ = ABC + AB C + ABC = ABC + ABC + AB C + ABC = = BC(A + A) + AC(B + B) = BC + AC.
Таблица 2.5
Таблица истинности для СДНФ
A |
B |
C |
F |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
FСКНФ = (A + B + C) × (A + B + C) × (A + B + C) × (A + B + C) × (A + B + C) =
=(A + B + C) × (A + B + C) × (A + B + C) × (A + B + C) × (A + B + C) × (A + B + C) =
=[( A + B) + C × C][( A + C) + B × B][(A + C) + B × B] = (A + B) × ( A + C) × (A + C).
Если требуется получить СКНФ функции, то из таблицы истинности считываются те состояния входных логических переменных, при которых функция принимает значение 0 (табл.2.5):
4. Заполнение карты Карно осуществляется следующим образом. Заданная функция приводится к СДНФ:
F= (AB) × (BC D ) × (B CD)(ABCD) = AB + BC D + B CD + ABCD
=AB + BC D + B CD + ABCD = FСДНФ.
32
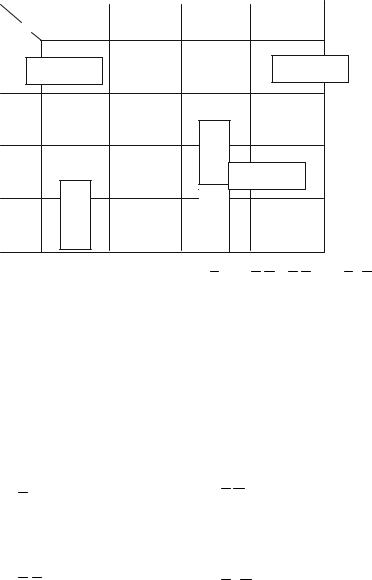
AB |
00 |
01 |
11 |
10 |
|
CD |
|||||
|
|
|
|
||
00 |
5 |
11,2 |
12 |
5 |
|
01 |
13 |
11 |
|
13 |
|
|
|
|
2 |
|
|
11 |
|
11 |
|
4 |
|
10 |
1 |
11 |
3 |
14 |
|
|
|
||||
Рис.2.7. Карта Карно для функции F = AB + BC D + B CD + ABCD |
|||||
|
|
(заполнение и считывание) |
|
||
В результате преобразования получается функция F в СДНФ на четыре входные переменные A,B,C,D. Рисуется карта Карно для четырех переменных (рис.2.7).
Приравнивая последовательно каждое слагаемое к 1, находятся те состояния входных переменных, при которых функция имеет значение 1.
ìA = 0
íB =1
AB =1 î
B CD = 1
ìB = 0 ïíC = 0 ïîD =1
BC D = 1
ABCD =1
ìB =1 ïíC = 0
ïîD = 0
ìA =1 ïïB = 0 íïC =1
ïîD = 0
33

Перед считыванием проводится упрощение логической функции. Если логическая функция записывается в СКНФ, то в карте Карно выполняется объединение соседних состояний с нулевыми значениями. В результате получается упрощенное выражение логической функции в СКНФ:
F = (A + B + C) × (A + B + D) × (A + B + C) × (A + C + D) × (B + C + D
.
34
