Министерство образования и науки Российской федерации

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

«Московский государственный институт электронной техники (технический университет)»

«УТВЕРЖДАЮ»

Декан факультета _ЭКТ_

______________ Путря М.Г.

«____» ______________200__г

Методические указания для подготовки к государственному экзамену по специальности по разделу «Моделирование технологических процессов».

для направления/специальности _210100.62 - Электроника и микроэлектроника

для факультета ЭКТ — Электроники и компьютерных технологий

форма обучения __очная_

КАФЕДРА ИЭМС — Интегральной электроники и микросистем

Составил:

д.т.н., проф. Крупкина Т.Ю.

Москва 2011

Содержание.

Введение………………………………………………………………………………... 1 Задачи курса «Моделирование технологических процессов» …………………… 2 Перечень типовых вопросов, выносимых на государственный экзамен………... 3 Методические материалы для подготовки к государственному экзамену ……… Литература…………………………..………………………………………………….

Введение

Развитие и использование математических моделей технологических процессов и создаваемых в результате их применения приборов является одной из основ современного подхода к проектированию интегральных схем и важной частью концепции компьютерно-интегрированного производства, т.е. имеет как научное, так и практическое значение. Необходимость моделирования технологических процессов и приборов обусловлена сложностью протекающих физических процессов, их многомерностью, нестационарным и неравновесным характером. С уменьшением критических размеров интегральных элементов роль моделирования многократно возрастает, т. к. усиливается взаимосвязь между электрофизическими характеристиками элементов и технологическими режимами изготовления интегральных схем и систем на кристалле.

Без изучения и освоения на практике принципов моделирования технологических процессов невозможно правильно спроектировать элементы интегральных схем, разработать технологию изготовления, спроектировать технологические маршруты и организовать производство. Знания в области моделирования технологических процессов позволяют на должном уровне выполнить необходимые исследования в ходе курсового проектирования по специальным дисциплинам и при работе над дипломным проектом.

Задачи курса «Моделирование технологических процессов».

Целью дисциплины является формирование знаний в области математического моделирования технологических процессов микроэлектроники, позволяющих глубже понимать сущность процессов, используемых в производстве изделий интегральной электроники, проектировать эти изделия на основе современных методов и с использованием современных компьютерных технологий.

В задачи изучаемой дисциплины входит:

• изучение основных физических явлений, используемых в процессах формирования элементов интегральных схем; математическое описание этих явлений с помощью основных уравнений, характеризующих процессы внедрения и перераспределения примеси в полупроводниковых материалах;

• изучение принципов численного моделирования технологических процессов и математических моделей основных технологических операций;

• формирование знаний в области достижений отечественной и зарубежной науки и техники в области математического моделирования технологических процессов микроэлектроники;

• формирование навыков по проведению численного моделирования процессов формирования основных интегральных структур, технологических маршрутов и отдельных технологических операций, анализу, систематизации и обобщению полученных расчетных данных, подготовки материалов для составления отчетов;

• обучение методам исследования объектов интегральной микроэлектроники на базе программных средств математического моделирования технологических процессов и современных компьютерных технологий.

Перечень типовых вопросов, выносимых на государственный экзамен

Ионная имплантация

1. Опишите основные механизмы торможения ионов при ионной имплантации. Приведите выражения, график зависимости от энергии иона

2. Чему равна полная средняя длина пробега иона в мишени? Поясните смысл параметров, входящих в уравнение.

3. Как рассчитывается проекция пробега иона в диффузионной модели Бирсака?

4. Что такое критический угол каналирования? Приведите выражение и графическую иллюстрацию.

5. Какие параметры должны учитываться в системе координат при моделировании ионной имплантации?

6. Аппроксимация распределения ионов в мишени по нормальному закону. Асимметричное распределение Гаусса. Приведите выражения, укажите смысл входящих параметров.

7. Параметры функции распределения Пирсон-IV. Проиллюстрируйте графически.

8. Приведите пример аналитической аппроксимации распределения ионов, учитывающей эффект каналирования.

Диффузия

9. Уравнения диффузии, определение коэффициента диффузии на макроскопическом и микроскопическом уровне.

10. Температурная зависимость коэффициента диффузии. Коэффициент диффузии для вакансионного механизма.

11. Основные уравнения модели связанной диффузии.

12. Граничные и начальные условия в моделировании диффузии.

13. Моделирование кластеризации примеси.

14. Модель кластеризации бора. Кластеры и преципитаты.

15. Модель кластеризации мышьяка.

16. Е-центры. Модель Файера-Цая для диффузии фосфора.

17. Примеры взаимного влияния примесей в процессе диффузии.

18. Особенности процесса постимплантационной диффузии. TED-эффект.

19. Особенности моделирования диффузии в поликристаллическом кремнии.

Окисление

20. Уравнение Дила-Гроува для термического окисления кремния. График зависимости толщины окисла от времени.

21. Константы линейного и параболического роста. Факторы, влияющие на значение констант.

22. Модель Массуда для начального этапа процесса окисления.

23. Основные процессы, учитываемые при численном моделировании окисления.

Травление, осаждение, фотолитография

24. Алгоритм струны при моделировании травления слоев.

25. Модель баллистического осаждения.

26. Основные этапы численного моделирования процесса литографии.

Методы численного моделирования

27. Запишите базовые уравнения численного моделирования полупроводниковых приборов в дрейфово-диффузионном приближении.

28. Запишите базовые уравнения численного моделирования полупроводниковых приборов для термодинамической модели.

29. Основные алгоритмы, используемые для дискретизации базовых уравнений при численном моделировании полупроводниковых приборов.

30. Перечислите основные факторы, определяющие сходимость численного решения.

Методические материалы для подготовки к государственному экзамену

1 Опишите основные механизмы торможения ионов при ионной имплантации.

При высоких энергиях ионов преобладает электронное торможение – неупругие столкновения со связанными электронами.

При низких энергиях имеет место электронное торможение и ядерное торможение – упругие столкновения с атомами, приводящие к частичной передаче кинетической энергии атомам.

Количественно эти механизмы характеризуются тормозной способностью – удельной потерей энергии атомом.

Ядерная тормозная способность

Sn(E) = - (1/N)(dE/dx)n =

Электронная тормозная способность

Se(E) = - (1/N)(dE/dx)e = kE ^1/2

где Е – энергия частицы, N – атомная плотность,

Tn – энергия, передаваемая при столкновении с атомом, Tn = Tmax sin2(φ/2),

Tmax – максимальная передаваемая энергия при лобовом столкновении,

Tmax = 4M1M2E/(M1+M2)², М1, М2 – массы иона и атома мишени, соответственно,

φ – угол рассеяния в системе центра масс, σ – дифференциальное сечение столкновения.

Рисунок 1 - Зависимость тормозной способности от энергии ионов

2 Чему равна полная средняя длина пробега иона в мишени?

Полная средняя длина пробега иона в мишени:

R =

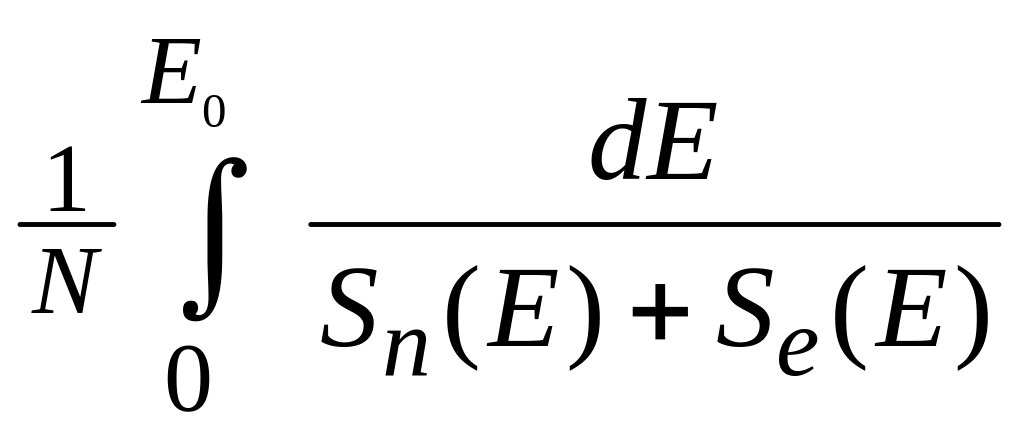
где Е0 – начальная энергия иона, Sn и Se – ядерная и электронная тормозная способность (предыдущий раздел).

3 Как рассчитывается проекция пробега иона в диффузионной модели Бирсака?

Средняя проекция пробега иона в диффузионной модели Бирсака.

Rp =

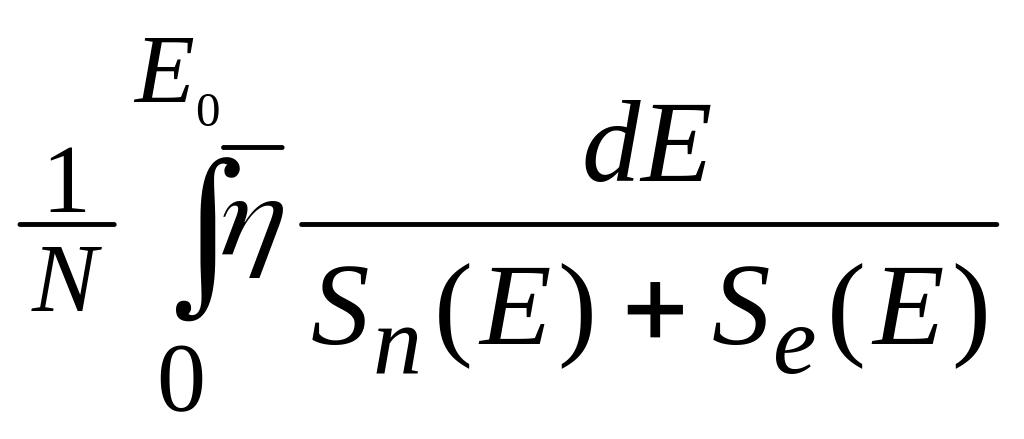
где - среднее значение направляющего косинуса ионной траектории, изменяющейся при столкновениях с атомами мишени, М1, М2 – массы иона и атома мишени, соответственно, Е0 – начальная энергия иона, Sn и Se – ядерная и электронная тормозная способность (вопрос 1);

= ;

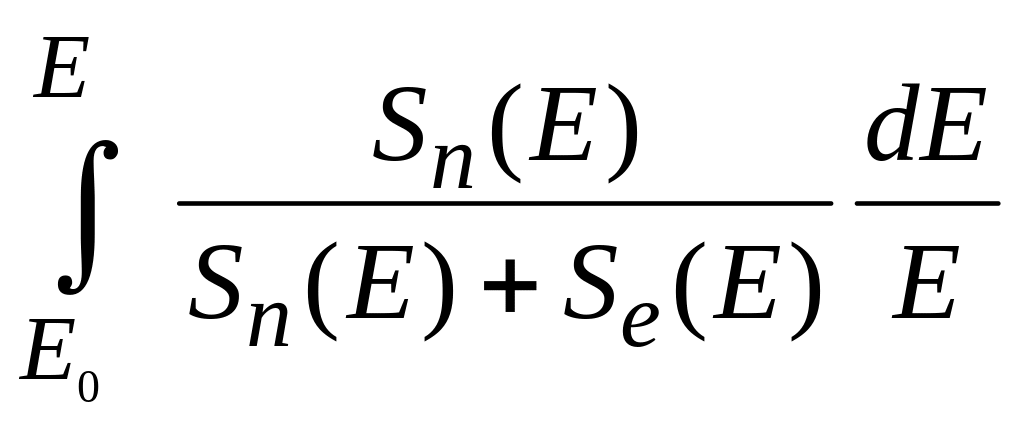
4 Что такое критический угол каналирования?

Критический угол каналирования – максимальный угол захвата ионов в канал при имплантации в кристаллическую подложку.

Ψкрит =

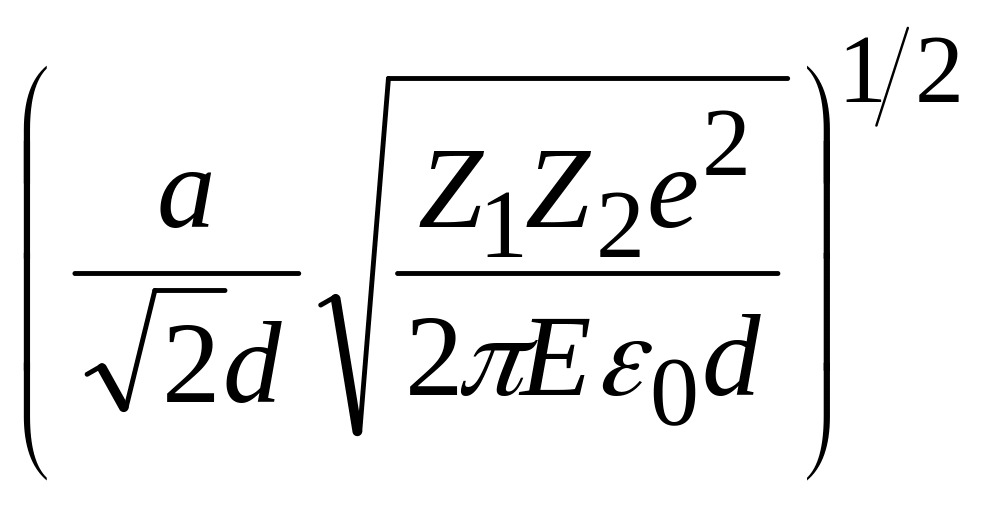
а – параметр экранирования порядка радиуса Бора, d – расстояние между атомами вдоль канала, Z1, Z2 – атомный номер иона и атома мишени, Е – энергия иона.

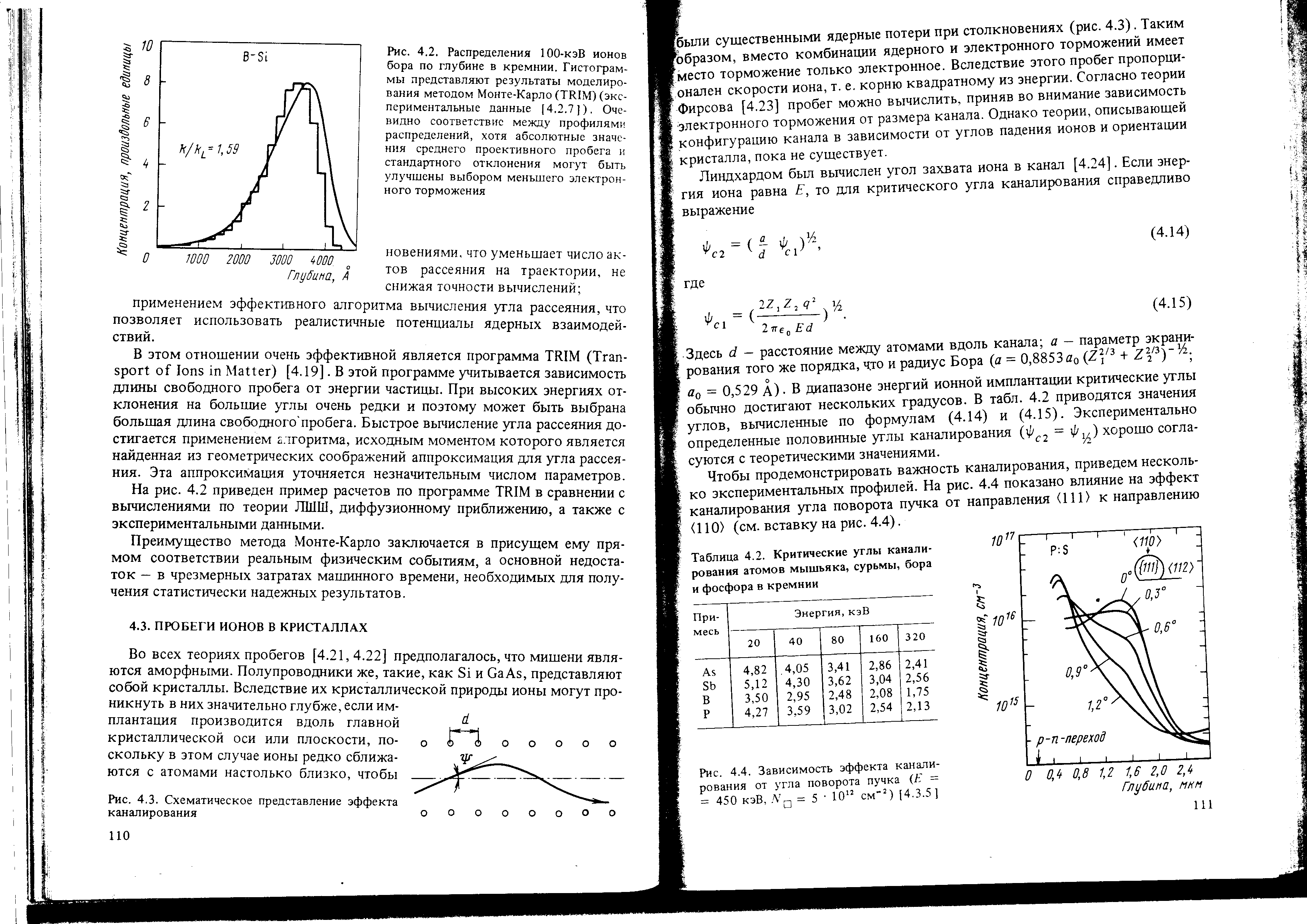
Рисунок 2 – Критический угол каналирования

5 Какие параметры должны учитываться в системе координат при моделировании ионной имплантации?

При моделировании ионной имплантации необходимо учитывать:

- параметры, определяющие положение пластины в установке ионной имплантации

tilt – угол наклона пластины, определяемый вращением вокруг базового среза,

rotation – угол вращения вокруг оси, перпендикулярной поверхности пластины;

- направление секущей линии при расчете двумерного сечения пластины относительно базового среза (задается координатами единичного вектора).

Стандартное положение пластины с углами Tilt = 7°, Rotation = -90° показано на рисунке 3.

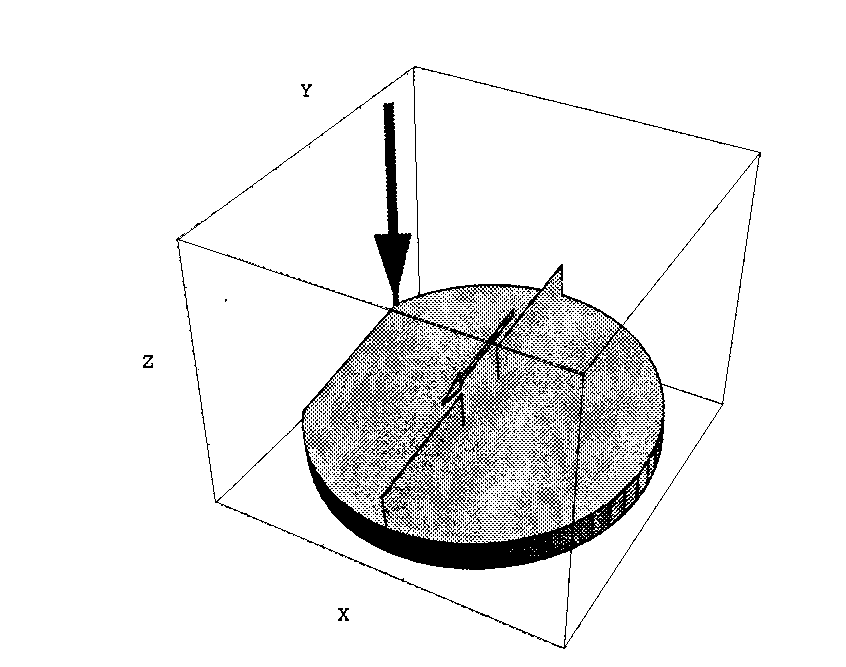
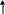
Рисунок 3 - Положение пластины в физической системе координат имплантера, задаваемое углами Tilt = 7°, Rotation = -90°, Cutline(0,0,1,0)

6 Аппроксимация распределения ионов в мишени по нормальному закону. Асимметричное распределение Гаусса.

Аппроксимация распределения ионов по нормальному закону

- распределение Гаусса:

N(x) = exp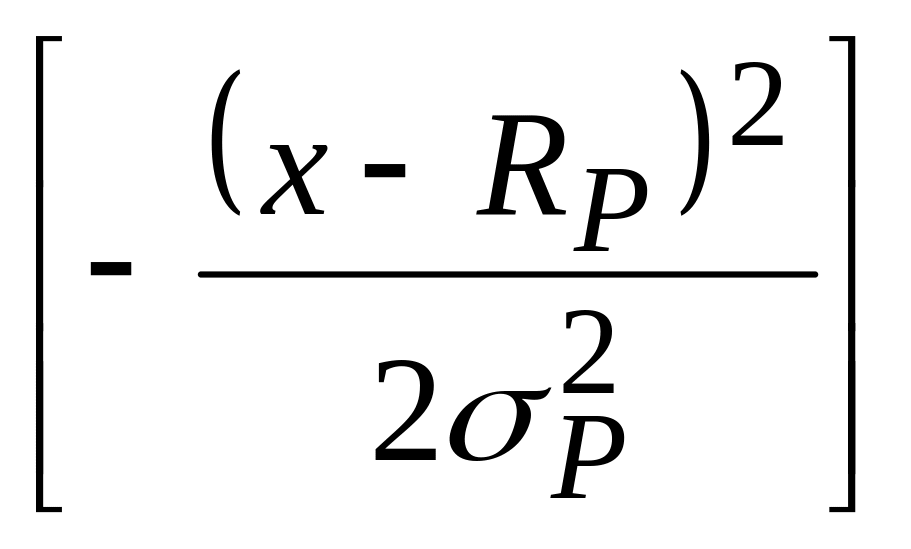

где D – доза имплантированной примеси, 1/ см-3, , - средняя проекция пробега ионов и среднеквадратичное отклонение проекции пробега, соответственно.

- двойное сопряженное распределение Гаусса (асимметричное):

N(x) =

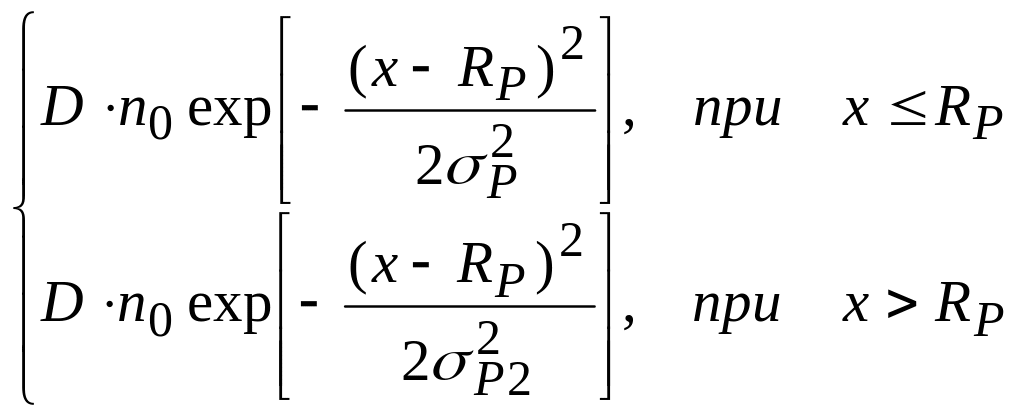
где = ;

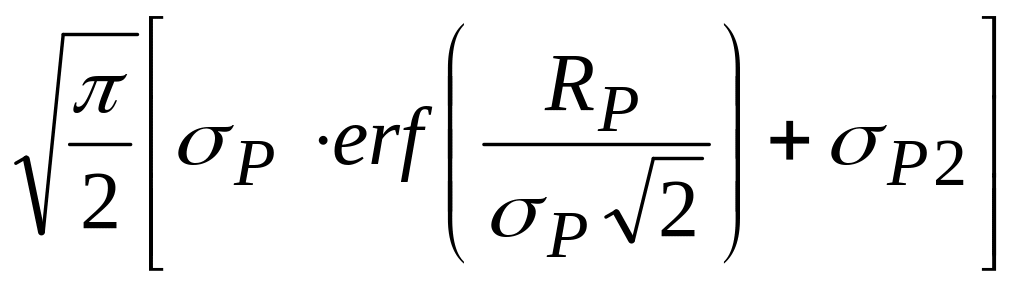7 Параметры функции распределения Пирсона-IV.

Функция распределения Пирсона-IV имеет 4 параметра, определяемые из первых четырех моментов

R_P = μ₁ = – средний проективный пробег, он же 1-ый момент функции распределения;

; i=2, 3, 4

σ_P = (μ₂)^1/2 – среднеквадратичное отклонение

- асимметрия;

эксцесс, характеризует плавность вблизи вершины.

Привести иллюстрацию функции распределения с γ = 0; N_MAX = N(R_P);

γ < 0; R_MAX > R_P;

γ > 0; R_MAX < R_P;

8 Приведите пример аналитической аппроксимации распределения ионов, учитывающей эффект каналирования.

распределение Гаусса с обобщенным экспоненциальным «хвостом»:

N(x) =

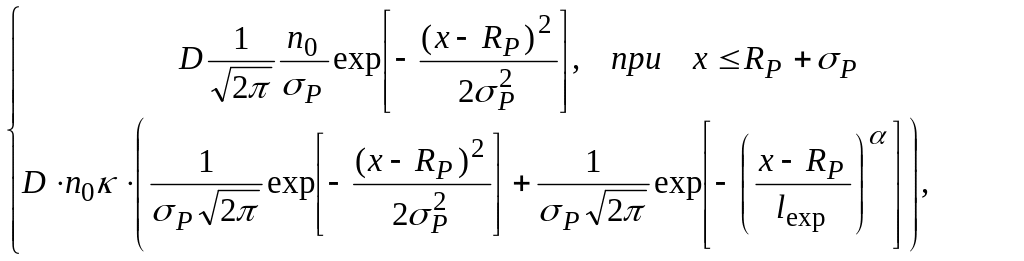
где D – доза имплантированной примеси, 1/ см-3, , - средняя проекция пробега ионов и среднеквадратичное отклонение проекции пробега, соответственно; k – коэффициент, обеспечивающий непрерывность в точке x = + ; n₀ – обратное значение нормы функции распределения, α, lexp – параметры распределения в «хвостовой» части. Привести иллюстрацию.

9 Уравнения диффузии, определение коэффициента диффузии на макроскопическом и микроскопическом уровне.

Первый закон Фика

,

где поток примеси, D – коэффициент диффузии, N – концентрация примеси.

В первый закон Фика входит коэффициент диффузии D в макроскопическом определении. В общем случае, это тензор 2-го ранга. Для симметричной кристаллической решетки кремния коэффициент диффузии может рассматриваться как скаляр.

В общем случае с учетом электрического поля

= - D gradN + ZμN_I E;

где Z – зарядовое состояние иона примеси, μ – подвижность примеси, N_I – концентрация электрически активной примеси, E – напряженность электрического поля.

Уравнение непрерывности для процесса переноса примеси с учетом электрических полей имеет вид:

Второй закон Фика вытекает из уравнения непрерывности для одномерного случая без учета электрических полей:

dN/dt = Dd²N/dx².

Для теоретического анализа микроскопических процессов в решетке удобно использовать микроскопическое определение коэффициента диффузии, например, компонента коэффициента диффузии по координате x как среднеквадратичное смещение атомов примеси за время Δt:

Dx= ( )² /Δt.