
- •Методические указания для подготовки к государственному экзамену по специальности по разделу «Моделирование технологических процессов».
- •10 Температурная зависимость коэффициента диффузии. Коэффициент диффузии для вакансионного механизма.
- •11 Основные уравнения модели связанной диффузии.
- •19 Особенности моделирования диффузии в поликристаллическом кремнии.
- •20 Уравнение Дила-Гроува для термического окисления кремния. График зависимости толщины окисла от времени.
- •Привести график X(t)
- •24 Алгоритм струны при моделировании травления слоев.
- •25 Модель баллистического осаждения.
- •26 Основные этапы численного моделирования процесса литографии.
- •27 Запишите базовые уравнения численного моделирования полупроводниковых приборов в дрейфово-диффузионном приближении.
- •28 Запишите базовые уравнения численного моделирования полупроводниковых приборов для термодинамической модели.
- •29 Запишите основные алгоритмы, используемые для дискретизации базовых уравнений при численном моделировании полупроводниковых приборов.
- •30 Перечислите основные факторы, определяющие сходимость численного решения.
19 Особенности моделирования диффузии в поликристаллическом кремнии.
Для разделения дозы, сегрегированной на границах, и дозы активной примеси внутри зерна используются коэффициенты, определяемые из геометрических моделей. Поликристаллический кремний рассматривается как набор малых монокристаллических областей, зерен, которые имеют различную кристаллографическую ориентацию, но формируют непрерывный слой. При моделировании разделяют процессы, которые идут в объеме зерен и на межзеренных границах. Границы зерен рассматриваются как объемные области с фиксированной толщиной δ. Форма зерна может быть выбрана либо столбиковая, с высотой H, равной толщине поликристаллического слоя (см. рисунок 6), либо кубическая, со стороной L.
H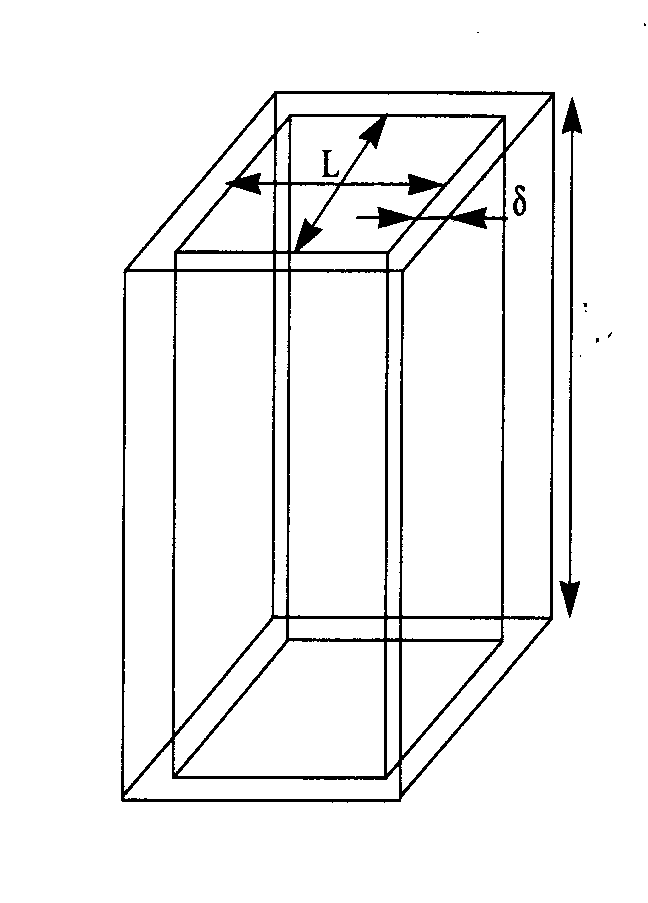
Рисунок 6 - Столбиковая модель зерна в поликристаллическом кремнии, L - размер зерна, δ – размер межзеренных областей, H - толщина поликристаллического слоя.
Доля объема поликристаллической пленки, приходящаяся на монокристаллические области внутри зерен выражается следующим образом:
- для столбиковой модели зерна
fg =
![]() ;
;
- для кубической модели зерна
fg =
![]() .
.
По коэффициенту fg рассчитывается доля межзеренных областей:
fgb = 1 - fg
Далее при моделировании высокотемпературных процессов в поликристаллическом кремнии учитывается рост зерен, приводящий к увеличению fg и уменьшению fgb, диффузия электрически активной примеси внутри монокристаллических зерен, электрически неактивной примеси вдоль границ и сегрегация примеси на поверхности зерен.
20 Уравнение Дила-Гроува для термического окисления кремния. График зависимости толщины окисла от времени.
Модель Дила-Гроува рассматривает процесс термического окисления кремния, как состоящий из двух этапов – массопереноса окислителя в растущем окисле и протекания химической реакции кремния с окислителем.
Модель рассматривает три потока. Привести иллюстрацию диаграммы высокотемпературного окисления кремния:
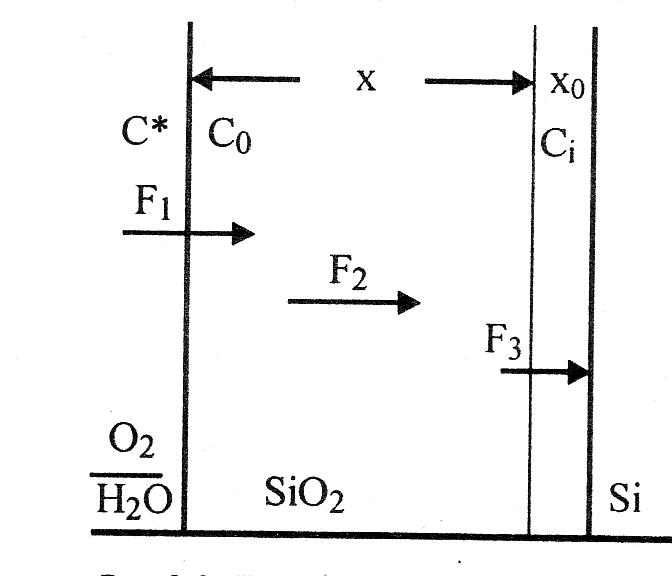
F1 = h(C*-C0) – массоперенос через внешнюю границу окисла, C*, C0 – концентрации окисляющих частиц;
F2 = D(C0 – Ci)/x – диффузия окислителя через окисел к границе раздела окисел/кремний.
F3 = kCi – химическая реакция на границе раздела окисел/кремний.
В условиях равновесия F1 = F2 = F3 , отсюда
![]() или
или
![]()
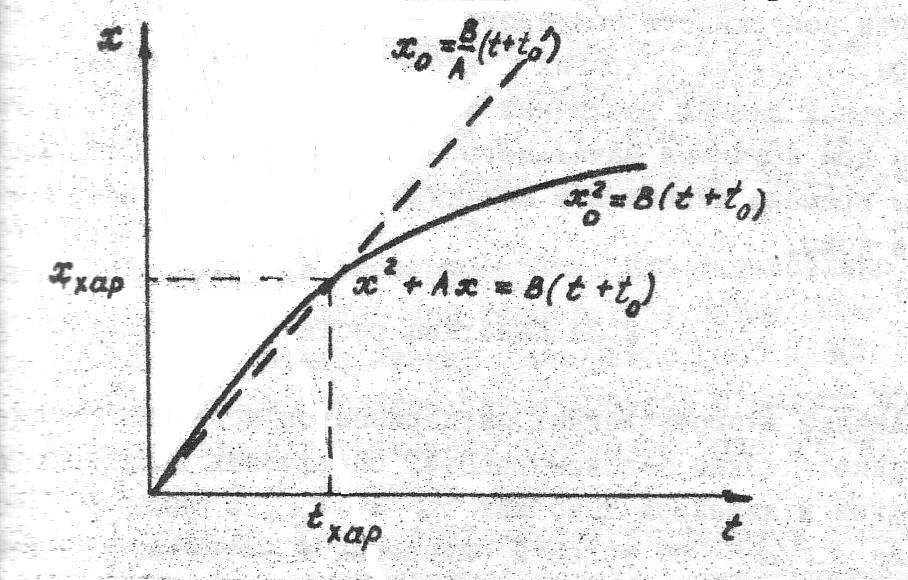
Интегрирование дает
x2 +Ax = B(t+t0)
или
![]()
Привести график X(t)
21 Константы линейного и параболического роста. Факторы, влияющие на значение констант.
В уравнение Дила-Гроува, описывающее рост окисла,
входят kP и kL – константы параболического и линейного роста, соответственно.
kP определяет диффузию окислителя через пленку,
kL определяет скорость химической реакции на границе раздела .
Влияющие факторы:
температура, по закону Аррениуса
kP = kP0 exp[-EP/kT],
kL = kL0 exp[-EL/kT].
-парциальное давление окислителя
kP от парциального давления зависит линейно, по закону Генри kP ~p;
kL ~pn; n=0.5 ÷ 1.0 в зависимости от температуры и окислительной среды.
наличие примеси в атмосфере: вода, натрий, хлор ускоряют окисление.
ориентация подложки: на kP практически не влияет;
kL (111) > kL (110) > kL (100).
22 Модель Массуда для начального этапа процесса окисления.
Для расчета тонких слоев окисла Массудом, Пламмером и Иреном была предложена модель, по форме близкая к модели Дила-Гроува (предыдущий вопрос), но позволяющая с более высокой точностью моделировать начальный этап окисления за счет введения дополнительных параметров С и τ, определяющих начальный этап роста окисла:
![]() .
.
Использование такой уточненной модели при моделировании роста подзатворного окисла дает результаты, хорошо совпадающие с экспериментальными данными.
23 Основные процессы, учитываемые при численном моделировании окисления.
Точное моделирование окисления и других термических операций, которые изменяют состав и структуру слоев должно включать моделирование следующих процессов:
- химические реакции на границах раздела слоев, состоящие из растворения частиц, - реакции частиц с материалом слоя, образование нового слоя;
- сегрегацию примеси на границах раздела слоев;
- диффузию примеси;
- экранирование потоков частиц слоями и границами раздела;
- механическую деформацию слоевой структуры как результат протекания химических реакций.
Для каждой границы раздела по коэффициентам протекающих химических реакций и соотношению удельных плотностей материалов слоев можно определить скорости образования/поглощения двух соседних слоев. Если на границе раздела скорости образования/поглощения компенсируют друг друга, то граница раздела просто движется через структуру. Если скорости не компенсированы, то реакция на границе является источником механических напряжений и деформаций.
Таким образом, расчет окислительного процесса подразделяется на несколько шагов:
- решение уравнения растворения – диффузии – химической реакции для частиц окислителя, т.е. расчет процесса диффузии частиц окислителя с граничными условиями на границах раздела в виде уравнений химических реакций/растворения;
- оценка скоростей образования и поглощения на границе раздела и определение граничных условий для расчета механических напряжений;
- расчет механических напряжений;
- вычисление граничных условий и решение уравнения диффузии примеси;
- расчет изменения толщин слоев;
- локальное обновление сетки в окрестности движущихся границ раздела, интерполяция концентраций, если необходимо, полное обновление сетки.
