27 Запишите базовые уравнения численного моделирования полупроводниковых приборов в дрейфово-диффузионном приближении.

Уравнение Пуассона div (εּgradψ) = -ρ;

Уравнения непрерывности: = div Jn + (G – R);

= div Jр + (G – R);

Уравнения переноса Jn = - qμ nּgrad φ ;

Jp = - qμ pּgrad φ ;

где ε – диэлектрическая проницаемость; ψ – электростатический потенциал; ρ – плотность объемного заряда; ρ = -qּ(n – p + N); n, p – концентрация электронов и дырок; N – алгебраически суммарная концентрация электрически активной примеси; Jn, Jp – плотность электронного и дырочного тока; (G – R) – суммарный вклад процессов генерации – рекомбинации носителей; μ , μ -подвижности электронов и дырок; φ , φ - квазиуровни Ферми для электронов и дырок.

28 Запишите базовые уравнения численного моделирования полупроводниковых приборов для термодинамической модели.

В термодинамическом приближении учитываются термоэлектрические эффекты, связанные с неоднородным распределением температуры.

Уравнение Пуассона div (εּgradψ) = -ρ;

Уравнения непрерывности: = div Jn + (G – R);

= div Jр + (G – R);

Уравнения переноса Jn = - qμ n (grad φ + grad T)

Jp = - qμ p (grad φ + grad T)

где ε – диэлектрическая проницаемость; ψ – электростатический потенциал; ρ – плотность объемного заряда; ρ = -qּ(n – p + N); n, p – концентрация электронов и дырок; N – алгебраически суммарная концентрация электрически активной примеси; Jn, Jp – плотность электронного и дырочного тока; (G – R) – суммарный вклад процессов генерации – рекомбинации носителей; μ , μ - подвижности электронов и дырок; φ , φ - квазиуровни Ферми для электронов и дырок, P_n, P_p – величины термоэдс для электронов и дырок, Т – температура (Т_n=T_p=T_L)

29 Запишите основные алгоритмы, используемые для дискретизации базовых уравнений при численном моделировании полупроводниковых приборов.

- метод конечных разностей (МКР);

• метод конечных элементов (МКЭ)

• триангуляция Делоне

В методе конечных разностей сетка состоит из линий, параллельных осям координат. Шаг сетки может меняться.

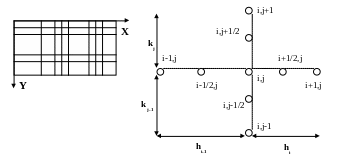
а)

б)

Рисунок 9 – Метод конечных разностей: а – вид сетки; б – схема дискретизации.

+ …

В методе конечных элементов сетка треугольная или комбинированная прямоугольно-треугольная.

Рисунок 10 Вид сетки при использовании метода конечных элементов.

Значение функции внутри элемента:

Для треугольника u^a(x,y) = a₀ + a₁x + a₂y;

для прямоугольника u^a(x,y) = a₀ + a₁x + a₂y + a₃xy;

значения коэффициентов определяются по значениям функции в узлах сетки.

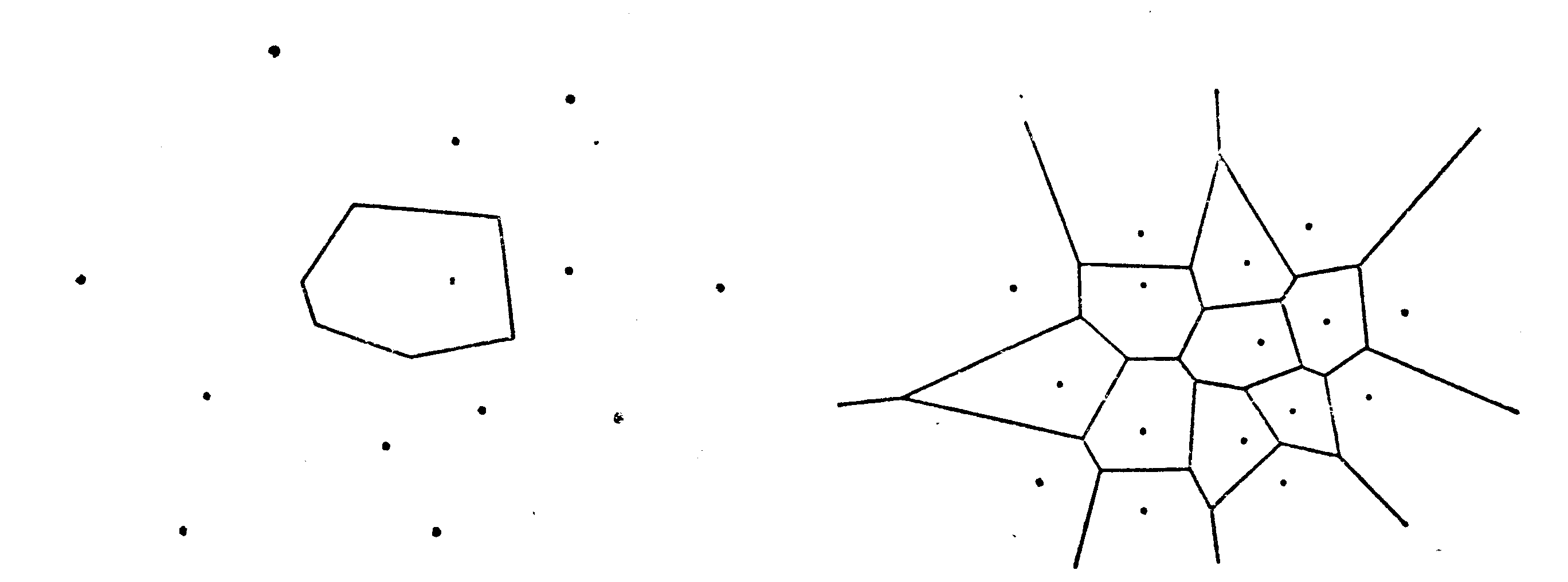
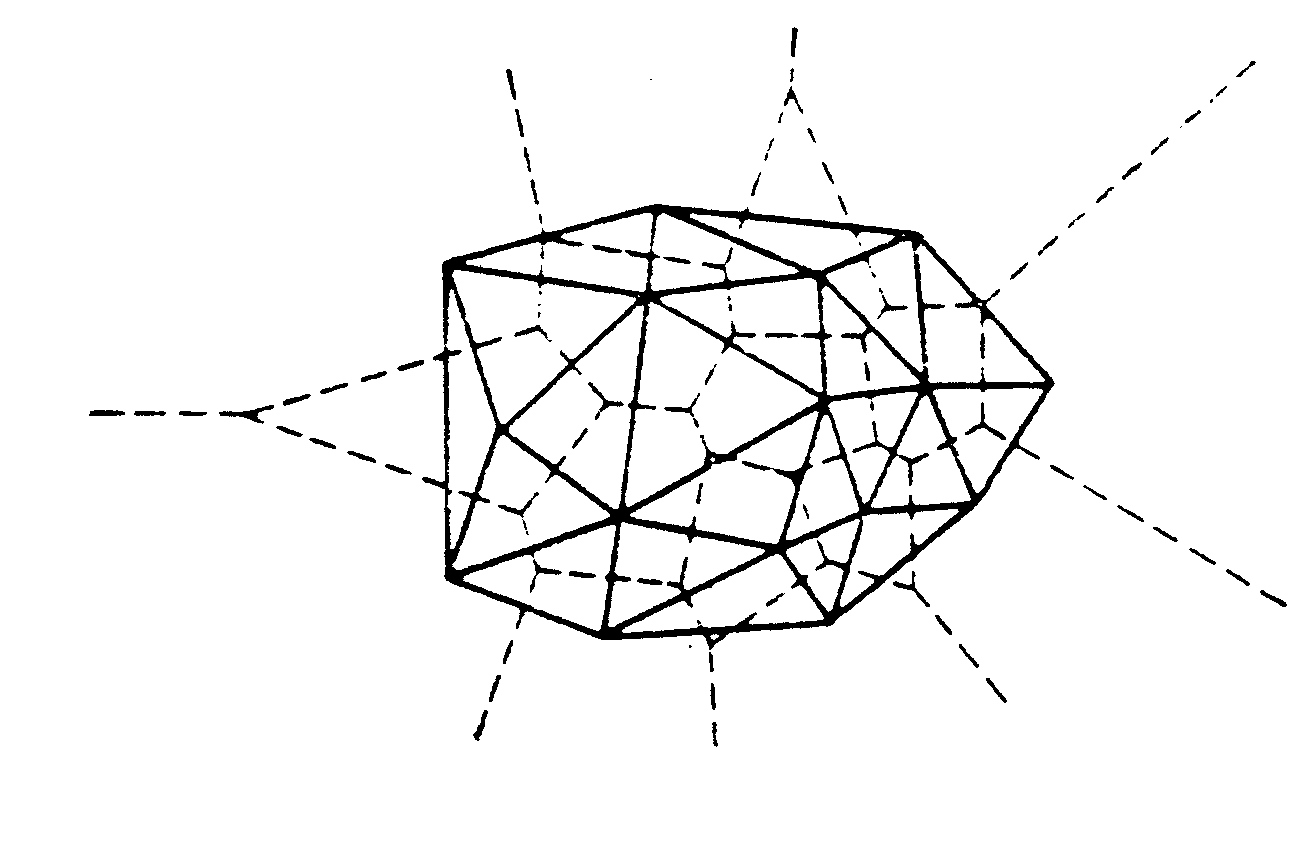
Триангуляция Делоне – построение, ортогональное разбиению Дирихле:

а)	б)

Рисунок 11 – Построение сетки методом триангуляции Делоне: а- разбиение Дирихле; б - триангуляция Делоне.

30 Перечислите основные факторы, определяющие сходимость численного решения.

Базовые дифференциальные уравнения для моделирования полупроводниковых приборов после дискретизации могут быть представлены как система большого числа нелинейных алгебраических уравнений F(x)=0.

Система может быть решена итеративно методом Ньютона

.

Точность вычислений может быть потеряна при расчете правой части и при расчете Якобиана. Количественно распространение ошибки вычислений задается коэффициентом усиления ошибки, который определяется для функции y(x) следующим образом:

Сходимость зависит от:

- разрядности вычислительной системы (машинная точность);

- коэффициента усиления ошибки при расчете правой части;

- коэффициента усиления ошибки при расчете Якобиана;

- особенностей решаемой физической проблемы

Литература

1. Королев М.А., Крупкина Т.Ю., Ревелева М.А. Технология, конструкции и методы моделирования кремниевых интегральных микросхем. Ч.1 Технологические процессы изготовления кремниевых интегральных схем и их моделирование. М., БИНОМ. Лаборатория знаний. 2007.

2. Королёв М. А., Крупкина Т. Ю., Путря М. Г., Шевяков В. И. Технология, конструкции и методы моделирования кремниевых интегральных микросхем, Ч. 2.- БИНОМ. Лаборатория знаний, 2009.

3. Артамонова Е.А., Балашов А.Г., Ключников А.С., Красюков А.Ю., Поломошнов С.А. Под ред. Крупкиной Т.Ю. Лабораторный практикум по курсу «Моделирование в среде TCAD». Ч.1 Введение в приборно-технологическое моделирование М.: МИЭТ, 2009

29