
- •Е.А.Коган
- •и естественно-научным дисциплинам
- •Москва 2010
- •Настоящее пособие посвящено двум важным и тесно связанным между собой разделам математики: обыкновенным дифференциальным уравнениям и вариационному исчислению.
- •Подробное изложение теории дифференциальных уравнений и вариационного исчисления содержится во многих учебниках и пособиях, некоторые из которых, рекомендуемые студентам втузов для самостоятельного изучения, приведены в списке литературы.
- •1.1. Основные понятия
- •Обыкновенное дифференциальное уравнение n-го порядка в самом общем виде записывается так:
- •Для дифференциальных уравнений первого порядка различают общее, частное и особое решения, а также общий, частный и особый интегралы.
- •Поэтому общее решение дифференциального уравнения можно определить как множество всех частных решений уравнения.
- •Особым решением дифференциального уравнения называется решение, которое не может быть получено из общего решения ни
- •при одном частном значении произвольной постоянной.
- •Часто при интегрировании уравнения первого порядка не удается найти его общее решение в явном виде, а получается конечное (не дифференциальное) соотношение вида
- •Знание изоклин позволяет во многих случаях даже для не интегрируемых явно дифференциальных уравнений получить графическое решение задачи Коши и выявить характер интегральных кривых.
- •Пример. Построить методом изоклин интегральную кривую уравнения
- •Таким образом, изоклинами данного уравнения являются концентрические окружности с центром в начале координат, причëм угловые коэффициенты касательных к искомым интегральным кривым равны радиусам этих окружностей С.
- •Очевидно, это уравнение с разделëнными переменными. Интегрируя его, получим
- •Следовательно, общий интеграл уравнения будет
- •Тогда
- •Тогда уравнение примет вид
- •Дифференциальное уравнение вида
- •называется приводящимся к однородному. В частности, к этому классу относится уравнение вида
- •В результате уравнение приводится к однородному
- •Возвращаясь к старой переменной, получим
- •Общее решение уравнения примет вид
- •После разделения переменных получим
- •Тогда уравнение (1.18) примет вид
- •Следовательно,
- •Подставляя (1.19) и (1.20) в (1.16), получим общее решение уравнения (1.12) в виде (1.15).
- •Уравнение вида
- •Следовательно, его общий интеграл, а значит, и общий интеграл уравнения (1.24) имеет вид
- •В результате общее решение уравнения будет иметь вид
- •После интегрирования получим
- •Следовательно, общее решение уравнения (2.18) будет
- •Далее ищем решение уравнения (2.17) в форме, аналогичной по структуре выражению (2.19), но произвольную постоянную в (2.19) заменяем неизвестной функцией
- •Подставляя (2.20) в (2.17), получим
- •В качестве практического примера применения метода понижения порядка рассмотрим задачу об осесимметричном изгибе упругих круговых пластин.
- •Определителем Вронского или вронскианом называется функциональный определитель вида:
- •Поэтому теорема о структуре общего решения линейного однородного дифференциального уравнения n-го порядка может быть переформулирована так:
- •а общее решение запишется в виде
- •Если известно общее решение однородного линейного дифференциального уравнения, соответствующего заданному неоднородному, то его частное решение может быть найдено методом вариации произвольных постоянных (методом Лагранжа).
- •Рассмотрим его реализацию для линейных дифференциальных уравнений второго порядка:
- •Интегрируя дифференциальные уравнения первого порядка (2.66), находим
- •Пример. Решить уравнение
- •Определитель этой системы
- •Интегрируя уравнения (2.71), находим
- •Подставляя (2.72) в (2.70), получим общее решение уравнения в виде
- •Рассмотрим линейное однородное дифференциальное уравнение второго порядка
- •Пример. Найти собственные значения и собственные функции однородной краевой задачи для уравнения (2.90) при граничных условиях
- •Общее решение уравнения согласно (2.92) имеет вид
- •Вычисляем
- •Раскрывая определитель, получим уравнение относительно параметра
- •корни которого являются собственными значениями задачи:
- •Уравнением Эйлера называется линейное уравнение вида
- •Пример. Решить уравнение
- •Уравнение (2.103) есть уравнение Эйлера второго порядка. Применим замену независимой переменной и производных по формулам (2.101), (2.102). Тогда уравнение примет вид
- •Его общее решение
- •Эти решения находятся методом подбора (см. выше) и имеют вид
- •Поэтому общее решение уравнения (2.104) будет
- •Пример. Решить задачу Коши для уравнения
- •Общее решение уравнения имеет вид
- •Убедимся в этом на примере системы двух уравнений относительно двух неизвестных функций
- •Будем искать частное решение однородной системы в виде
- •Пример. Решить методом Эйлера систему
- •Характеристическое уравнение системы
- •Общее решение однородной системы (3.18) запишется в виде
- •Этот метод применим к решению систем неоднородных линейных уравнений n-го порядка. Ограничимся для простоты нормальной системой двух линейных уравнений с постоянными коэффициентами
- •Пусть общее решение однородной системы уравнений известно:
- •Пример. Решить систему
- •Принимаем частное решение системы (3.31) в виде
- •Интегрируя эти уравнения, получим
- •Общее решение системы запишется в виде:
- •Пусть требуется решить краевую задачу для уравнения
- •Будем искать решение задачи в виде
- •Задача сводится к решению дифференциального уравнения
- •Выбранные функции удовлетворяют всем перечисленным выше требованиям. Они линейно независимы, непрерывно дифференцируемы и удовлетворяют граничным условиям (4.12).
- •Решение методом Бубнова
- •Как видим, ошибка, полученная при решении методом Бубнова в двучленном приближении, составляет сотые доли процента.
- •Решение методом наименьших квадратов
- •Решение методом коллокаций
- •В результате находим
75
|
−4A + 2C =1, |
|
|
|
A −4B + 4C + 2D = 0, |
|
|
|
2A + 4C = 0, |
|
|
|
−4A −2B +C −4D = 0. |
Из первого и третьего уравнений системы следует: A = −0,2, |
|
C = 0,1. |
Поэтому из второго и четвертого уравнений находим |
B = 0,13, |
D = 0,16. Таким образом, искомое частное решение за- |
пишется в виде
y = (−0,2x +0,13)cos 2x +(0,1x +0,16)sin 2x.
Складывая его с общим решением однородного уравнения, окончательно получим общее решение исходного уравнения
y= C1 +C2e−x + (−0,2x +0,13)cos 2x +(0,1x +0,16)sin 2x.
2.4.2.Метод вариации произвольных постоянных
Если известно общее решение однородного линейного дифференциального уравнения, соответствующего заданному неоднородному, то его частное решение может быть найдено методом вариации произвольных постоянных (методом Лагранжа).
Рассмотрим его реализацию для линейных дифференциальных уравнений второго порядка:
y′′+ a1 y′+ a2 y = f (x). |
(2.59) |
Сначала находим общее решение соответствующего линейного однородного уравнения L(y) = 0 в виде
y0 = C1 y1 + C2 y2, |
(2.60) |
где C1 и C2 - произвольные постоянные, y1 , |
y2 - частные линейно |
независимые решения однородного уравнения.
Далее ищем решение неоднородного уравнения (2.59), аналогичное по структуре (2.60), но произвольные постоянные в (2.60) заменяем неизвестными функциями, а именно принимаем
y = C1 (x)y1 + C2 (x)y2. |
(2.61) |
Тогда y′ = C1′(x)y1 +C1 (x)y1′ +C2′(x)y2 +C2(x)y2′.

76
Так как функции C1 (x) и C2(x) произвольны, то можно принять,
что они должны удовлетворять условию: |
|
C1′(x)y1 +C2′(x)y2 = 0. |
(2.62) |
Тогда y′ = C1 (x)y1′ +C2(x)y2′ и, следовательно, |
|
y′′ = C1′(x)y1′ +C1 (x)y1′′+C2′(x)y2′ +C2(x)y2′′. |
(2.63) |
Подставляя теперь значения производных в уравнение (2.59), получим
C1 (x)(y1′′+ a1 y1′ + a2 y1 )+C2(x)(y2′′ + a1 y2′ + a2 y2 )+ |
(2.64) |
||
+C1′(x)y1′ +C2′(x)y2′ = f (x). |
|||
|
|||
Учитывая, что функции y1 |
и y2 являются решениями одно- |
||
родного уравнения (2.59), и, следовательно, |
|
||
y1′′+ a1 y1′ + a2 y1 = 0, |
y2′′ + a1 y2′ + a2 y2 = 0, |
|
|
приходим к равенству |
|
|
|
C1′(x)y1′ +C2′(x)y2′ = f (x).
Таким образом, чтобы выражение (2.61) было решением неоднородного уравнения (2.59), неизвестные функции C1 (x) и
C2(x) должны удовлетворять следующей системе дифференциальных уравнений
C′(x)y |
|
+C′ |
(x)y |
|
= 0, |
(2.65) |
|||
1 |
1 |
2 |
|
|
|
2 |
= f (x). |
||
C1′(x)y1′ +C2′(x)y2′ |
|
||||||||
Определитель этой системы - определитель Вронского |
|
||||||||
W = |
|
y1 |
y2 |
|
≠ 0, |
|
|||
|
|
|
|||||||
|
|
|
y2′ y2′ |
|
|
|
|
|
|
так как функции y1 и y2 |
линейно независимы. Поэтому система |
||||||||
(2.65), рассматриваемая как система линейных алгебраических уравнений относительно С1′(x), С2′(x), имеет решение и притом
единственное. Применяя формулы Крамера11, его можно предста-
11 К р а м е р Габриэль (31.07.1704 – 04.01.1752) – швейцарский математик.
77
вить в виде
C1′(x) = − |
y2 f (x) |
, |
C2′(x) = |
y1 f (x) |
. |
(2.66) |
|
|
|||||||
W |
|||||||
|
|||||||
|
|
|
W |
|
|||
Интегрируя дифференциальные уравнения первого порядка (2.66), находим
С (x) = − |
∫ |
y2 f (x) |
dx +C , |
C (x) = |
∫ |
y1 f (x) |
dx + C . |
(2.67) |
|||||||||
|
|||||||||||||||||
|
|
||||||||||||||||
1 |
|
W |
|
1 |
|
|
2 |
|
|
W |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставляя (2.67) |
в (2.61), |
получим общее решение неод- |
|||||||||||||||
нородного уравнения в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
∫ |
y2 f (x) |
|
|
|
∫ |
y1 f (x) |
|
|
|||
|
y = C1 y1 + C2 y2 |
− y1 |
W |
|
dx + y2 |
W |
dx. |
(2.68) |
|||||||||
|
|
|
|
|
|
|
|
||||||||||
Последние два слагаемых в правой части формулы (2.67) определяют частное решение неоднородного уравнения (2.59).
Таким образом, если известна фундаментальная система решений соответствующего линейного однородного уравнения y1 , y2, то общее решение неоднородного уравнения может быть
найдено с помощью квадратур (то есть неопредёленных интегралов от этих решений).
Замечание. Метод вариации произвольных постоянных является общим методом, пригодным для построения решения линейных неоднородных дифференциальных уравнений (как с переменными, так и с постоянными коэффициентами) при произвольной непрерывной правой части. Но он является принципиально более сложным, чем метод подбора, так как его реализация связана с интегрированием дифференциальных уравнений первого порядка. Поэтому для линейных неоднородных уравнений с постоянными коэффициентами и с правыми частями специального вида, указанными в таблице 2, проще применять метод подбора частного решения.
Пример. Решить уравнение
|
′′ |
|
′ |
e−2x |
|
|
y |
+ 4 y |
+ 4 y = x . |
(2.69) |
|||
|
|
1). Находим общее решение соответствующего однородного уравнения
78
y′′+ 4 y′+ 4 y = 0.
Составляем характеристическое уравнение k 2 + 4k + 4 = 0.
Его корни k1 = k2 = −2. |
Следовательно, частные линейно незави- |
||||
симые решения равны |
y = e−2x , |
y |
2 |
= xe−2x , |
а общее решение |
|
1 |
|
|
|
|
y0 = C1e−2x +C2xe−2x .
2). Так как правая часть неоднородного уравнения (2.69) не относится ни к одному из рассмотренных в таблице 2 случаев, то частное решение находим методом вариации произвольных постоянных. Принимаем
y = C (x)e−2x + C |
2 |
(x)xe−2x , |
(2.70) |
1 |
|
|
где C1 (x) и C2 (x) - неизвестные (варьируемые) функции. Тогда
их производные C1′ (x) и C2′(x) могут быть найдены из решения системы (2.65):
′ |
(x)e |
−2x |
|
|
′ |
|
−2x |
= 0, |
|
|
|
|
|
||
C1 |
|
|
+ C2 (x)xe |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
−2x |
|
|
− 2C1′(x)e−2x + C2′(x)(e−2x − 2xe−2x ) = e |
x |
. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определитель этой системы |
|
|
|
|
|
|
|
|
|
||||||
|
W = |
|
|
e−2x |
xe |
−2x |
|
= e−4 x . |
|
|
|
||||
|
|
|
|
|
|
|
|||||||||
|
− |
2e−2x |
e−2x |
|
− 2xe−2x |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
Поэтому для определения варьируемых функций согласно |
|||||||||||||||
(2.66) получаем дифференциальные уравнения вида |
|
|
|||||||||||||
C1′(x) = − xe−2xe−2x |
= −1, |
|
C2′(x) = e−2xe−2x |
= |
1 . |
(2.71) |
|||||||||
|
xe−4 x |
|
|
|
|
|
|
|
xe−4 x |
|
x |
|
|||
Интегрируя уравнения (2.71), находим |
|
|
|
|
|
||||||||||
C1 (x) = −x + C1 , |
C2 (x) = ln x + C2. |
|
|
(2.72) |
|||||||||||
Подставляя (2.72) в (2.70), получим общее решение уравнения в виде
y = e−2x [C1 + C2x + x(lnx −1)].
79
2.5.Вынужденные колебания линейной системы
содной степенью свободы без учета сил сопротивления
Клинейным дифференциальным уравнениям с постоянными коэффициентами сводятся многие задачи о механических и электрических колебаниях.
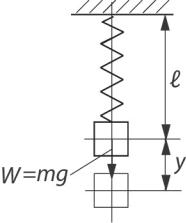
1) В качестве первого практического примера применения изложенной теории рассмотрим задачу о вынужденных колебаниях линейной системы с одной степенью свободы без учета сил сопротивления. Такой системой моделируются вертикальные перемещения груза массой m на пружине (см. рис. I.8). Массой пружины по сравнению с массой груза пренебрегается.
Если сообщить грузу некоторую начальную скорость и начальное отклонение, то под действием восстанавливающей силы упругости пружины система будет совершать колебания относительно положения статического равновесия, называемые собст-
венными или свободными колебаниями.
Рис. I.8
Удлинение пружины при действии статически приложенного груза W = mg равно
δст = mg |
, |
(2.73) |
k |
|
|
где k - коэффициент жëсткости пружины (груз, вызывающий ëе удлинение, равное единице) [16].
Если y - вертикальное перемещение колеблющегося груза
относительно положения статического равновесия (оно считается положительным, если направлено вниз), то уравнение движения
80
груза при его свободных колебаниях согласно второму закону Ньютона запишется в виде
|
|
|
|
|
m d 2 y = mg −k(y +δст ) |
|
||
|
|
|
|
|
|
dt2 |
|
|
или после подстановки выражения (2.73) |
|
|||||||
|
|
|
|
|
|
d 2 y + p2 y = 0, |
(2.74) |
|
где |
|
|
|
|
|
dt2 |
|
|
|
k |
|
|
g |
|
|
||
t - время, а |
p2 = |
= |
|
- квадрат круговой частоты собственных |
||||
m |
|
|||||||
|
|
|
δст |
|
||||
колебаний системы.
Пусть кроме силы веса и силы натяжения пружины на груз действует периодическая возмущающая сила P(t) = F sin ωt , вы-
зывающая вынужденные колебания системы (F – амплитуда, ω - частота вынужденных колебаний),
Тогда дифференциальное уравнение движения груза запишется в виде
md 2 y = mg −k(y +δст )+ F sin ωt dt2
или
m d 2 y + ky = F sin ωt. dt2
Полагая q = mF , получим окончательно уравнение вынуж-
денных колебаний одномассовой системы в виде линейного неоднородного дифференциального уравнения с постоянными коэффициентами второго порядка:
y′′+ p2 y = q sin ωt. |
(2.75) |
|
Решаем сначала однородное уравнение |
y′′+ p2 y = 0. |
Ха- |
рактеристическое уравнение, ему соответствующее: k 2 + p2 |
= 0, |
|
имеет мнимые корни k1,2 |
= ±pi . Поэтому общее решение одно- |
|
родного уравнения запишется в виде |
|
|
y0 |
= C1 cos pt +C2 sin pt. |
(2.76) |

81
Полагая C1 = Asinϕ, C2 = Acosϕ, можно представить решение (2.76) в виде
y0 = Asin(pt +ϕ).
Это решение описывает собственные колебания массы m относительно положения статического равновесия. Как видно, колебания являются незатухающими и происходят по синусои-
дальному закону с амплитудой A, периодом τ = 2pπ = 2π 
 mk и на-
mk и на-
чальной фазой ϕ. При этом величина, обратная периоду - так на-
зываемая техническая частота колебаний (число колебаний в секунду), равна
ν=τ1 = 2pπ
иизмеряется в герцах. Тогда число колебаний в 1 мин. будет рав-
но
|
60p |
|
60 |
|
|
|
|
|
300 |
|
, |
n = |
= |
|
g |
= |
|||||||
2π |
2π |
δст |
|
|
|
||||||
|
|||||||||||
|
|
|
|
|
fст |
||||||
где fст - в см. Этой формулой пользуются в расчëтах в тех случа-
ях, когда система может быть сведена к системе с одной степенью свободы.
Частное решение уравнения (2.75) ищем методом подбора в
виде
y = B cosωt +C sin ωt.
Находя неопределëнные коэффициенты B и C, получим
y |
|
= |
F sin ωt |
|
|
= |
q sin ωt |
|
(2.77) |
|||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
ω |
2 |
|
|
|
|
|
ω2 |
|
|
||
|
|
|
mp2 |
− |
|
p2 |
− |
|
||||||||
|
|
|
1 |
|
2 |
|
|
1 |
|
2 |
|
|
||||
|
|
|
|
|
|
p |
|
|
|
|
|
p |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и окончательно, общее решение уравнения колебаний запишется в виде
y = C1 cos pt +C2 sin pt + |
|
q |
|
|
|
sin ωt. (2.78) |
|
p2 |
|
ω2 |
|
||||
|
|
||||||
|
1− |
|
2 |
|
|
||
|
|
|
p |
|
|
||
|
|
|
|
|
|
||
Последнее слагаемое описывает так называемый установив-

82
шийся режим вынужденных колебаний системы с частотой ω.
Подставляя в (2.77) выражения для p2 |
и |
q, получим |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
y = |
|
q sin ωt |
|
= |
|
m sin ωt |
|
= |
F |
|
|
1 |
|
sin ωt. (2.79) |
|||||||||
|
|
|
|
ω2 |
|
|
|
|
k |
|
|
|
ω2 |
||||||||||
|
p |
2 |
|
|
|
k |
|
ω2 |
|
1 |
− |
|
|||||||||||
|
|
|
− |
|
2 |
|
|
|
|
|
− |
|
2 |
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
1 |
|
p |
|
|
|
|
1 |
|
p |
|
|
|
|
|
|
p |
|
||||
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
||||
Множитель |
|
F |
характеризует перемещение, которое вызы- |
||||||||||||||||||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вает максимальная возмущающая сила, если она приложена ста-
тически, а множитель kдин = |
1 |
характеризует динамич- |
|
|
1−ω2 / p2 |
||
ность действия этой силы. Абсолютная величина этого множите-
ля называется коэффициентом динамичности.
Как видно из полученного решения, когда отношение ω / p →1, коэффициент динамичности и амплитуда колебаний
неограниченно возрастают. Это явление совпадения частоты возмущающей силы с частотой собственных колебаний системы на-
зывается резонансом.
2) Вынужденные колебания упруго подвешенного груза могут быть вызваны также другим способом, например, если верхнему концу пружины задать в вертикальном направлении простое гармоническое движение (см. рис. I.8)
y1 = C sin ωt. |
(2.80) |
Решение этой задачи дано С.П.Тимошенко12 [16].
Тогда удлинение пружины в произвольный момент времени будет равно y +δст − y1, а соответствующая сила упругости пру-
жины: mg + k(y − y1 ) (перемещение груза y при этом в любой
момент времени отсчитывается от положения равновесия, в котором y1 = 0). Поэтому уравнение движения подвешенного на пру-
жине груза запишется в виде
12Т и м о ш е н к о Степан Прокофьевич (22.12.1878 –29.05.1972)
–российский ученый и инженер в области механики деформируемого твердого тела.
83
|
m d 2 y = mg −k(y +δ |
ст |
− y ) |
|
|
|
||||
|
dt2 |
|
|
|
1 |
|
|
|
||
или |
|
|
|
|
|
|
|
|
||
|
d 2 y |
|
|
|
|
|
|
|||
|
m |
+ k(y − y )= 0. |
(2.81) |
|||||||
|
|
|||||||||
|
|
dt |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
||
Подставляя y |
в уравнение |
|
(2.81) и обозначая |
q = C |
, полу- |
|||||
|
|
|||||||||
1 |
|
|
|
|
|
|
|
m |
||
чим |
|
|
|
|
|
|
|
|
||
d 2 y |
|
|
|
|
|
|
|
|
||
|
+ p2 y = q sin ωt. |
(2.82) |
||||||||
|
dt2 |
|
|
|
|
|
|
|
|
|
Уравнение (2.82) совпадает с уравнением (2.75) при F = Ck. Следовательно, заданное гармоническое перемещение верхнего конца пружины C sin ωt можно рассматривать как эквивалентное
приложению возмущающей силы Ck sin ωt. Поэтому установив-
шийся режим вынужденных колебаний при перемещении верхнего конца пружины по принятому гармоническому закону будет описываться равенством, аналогичным равенству (2.79):
y = |
F 1 |
sin ωt = C |
1 |
sin ωt. |
(2.83) |
|||||
|
|
|
|
|
|
|||||
k 1− |
ω2 |
1− |
ω2 |
|||||||
|
|
|
|
|||||||
|
|
|
p2 |
|
|
|
p2 |
|
|
|
Используя решение задачи 2), легко получить решение следующей задачи [16]:
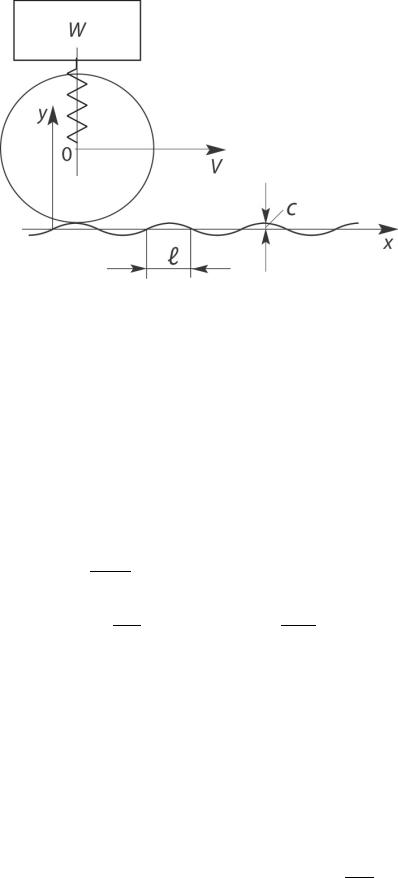
3) Пусть колесо катится с постоянной горизонтальной скоростью V =18 м/ с по неровной дороге, профиль которой задан
уравнением y = C sin |
πx |
, где C = 2,5см, а |
l = 90см (см. рис. I.9). |
|
l |
|
|
Найти амплитуду вынужденных вертикальных колебаний груза W = mg , связанного пружиной с осью колеса, если статическое
удлинение пружины под действием груза составляет δст = 9,8см.
Рассматривая свободные |
|
вертикальные колебания груза |
||||
W на пружине, найдем квадрат угловой частоты этих колебаний |
||||||
p2 = |
g |
|
= |
981=100 |
1 |
. |
|
|
сек2 |
||||
δст |
|
9,8 |
|
|||
84
Рис. I.9
Центр O катящегося колеса совершает вертикальные колебания ввиду неровности профиля дороги.
Пусть в начальный момент времени t = 0 точка касания колеса с дорогой находится в начале координат y = 0. Тогда, учи-
тывая, что y =Vt , получим для вертикальных колебаний этой точки равенство y = C sin πVtl . Поэтому вынужденные колебания груза можно определить из равенства (2.83) после подстановки в него значений p2 =100 сек1 2 , C = 2,5см,
ω= πlV =180090π = 20π сек1 ..
Врезультате амплитуда вынужденных колебаний колеса
будет равна (в этих вычислениях масса колеса не учитывается)
ymax = |
|
|
|
2,5 |
|
|
= 0,066см. |
|
|
1− |
(20π)2 |
|
|
||
|
|
||||||
|
|
|
|
100 |
|
|
|
Как видно, при заданной скорости движения вертикальные колебания колеса лишь в очень малой степени передаются грузу.
При уменьшении скорости V , в конце концов, при πlV = p можно

85
придти к резонансу; при этом будут очень сильные колебания груза.
2.6.Вынужденные колебания линейной системы
содной степенью свободы с учетом сил сопротивления
Если колеблющееся тело при движении испытывает сопротивление, пропорциональное скорости (это простейший случай так называемого вязкого трения, при котором сила трения
R = c dydt ), и кроме того, на него действует возмущающая сила
F sin ωt , то уравнение вынужденных колебаний системы с одной степенью свободы записывается в виде [16]
d 2 y |
+ 2n dy |
+ p2 y = |
F sin ωt , |
(2.84) |
||||
dt2 |
|
dt |
|
m |
|
|||
где |
|
k |
|
|
|
c |
|
|
|
p2 = |
, |
2n = |
. |
(2.85) |
|||
|
|
|
||||||
|
|
m |
|
|
m |
|
||
В (2.85) c–постоянная, равная величине демпфирующей силы при скорости, равной единице.
Однородное уравнение, соответствующее уравнению (2.85), описывает малые свободные колебания с учетом вязкого трения.
Характеристическое уравнение λ2 + 2nλ + p2 = 0 имеет кор-
ни λ |
= −n ± |
|
n2 − p2 |
. Будем различать три случая. |
1,2 |
|
n > p (случай большого сопротивления), то оба |
||
1) |
Если |
|||
корня действительны и отрицательны. Общее решение однородного уравнения запишется в виде
y0 = C1eλ1t +C2eλ2t = C1e(−n+
 n2−p2 ) t +C2e(−n−
n2−p2 ) t +C2e(−n−
 n2−p2 ) t =
n2−p2 ) t =
=e−nt (C1e
 n2−p2 t +C2e−
n2−p2 t +C2e−
 n2−p2 t ).
n2−p2 t ).
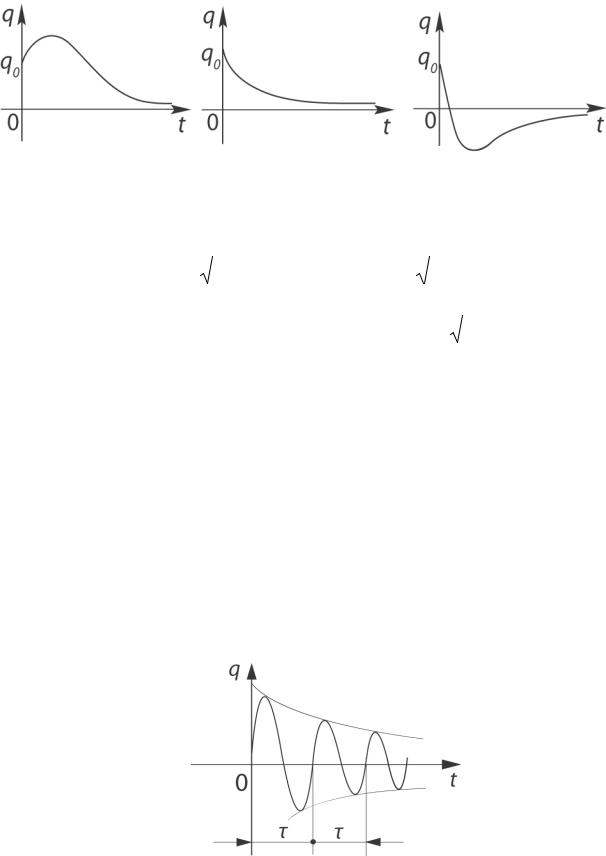
Сростом времени t отклонение y0 → 0, то есть система
асимптотически приближается к исходному невозмущëнному равновесному состоянию. Движение при этом не будет колебательным, а носит так называемый апериодический характер, хотя может реализовываться по – разному (см. рис. I.10).
86
Рис. I.10
2) Если n < p (случай малого сопротивления), то корни характеристического уравнения будут комплексно сопряжëнными:
λ = −n +i p2 −n2 , |
λ |
2 |
= −n −i p2 |
−n2 |
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
λ = −n +ir, |
|
λ |
2 |
= −n −ir, |
|
где |
r = |
|
p2 −n2 |
. (2.86) |
||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Общее решение уравнения (2.86) |
при этом будет |
|
|
|
||||||||
y |
0 |
= C e−nt cos rt +C |
e−nt sin rt , |
(2.87) |
||||||||
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
и если принять C1 = Asinϕ, C2 = Acosϕ, (где |
A,ϕ - постоянные), |
|||||||||||
оно может быть приведено к виду |
y0 |
= Ae−nt sin(rt +ϕ). |
||||||||||
Множитель e−nt убывает со временем, поэтому при малом трении происходят собственные колебания с амплитудой, убывающей со временем, так называемые затухающие колебания (см.
рис. I.11).
Частное решение неоднородного уравнения (2.84) находим методом подбора. Принимаем
y = M sin ωt + N cosωt, |
(2.88) |
Рис. I.11

87
где M и |
N - неопределëнные коэффициенты. Подставляя (2.88) |
||||||||
в уравнение (2.84) и приравнивая коэффициенты при |
sin ωt и |
||||||||
cosωt, получим |
|
|
|
|
|
||||
M = |
P |
|
p2 −ω2 |
N = − |
P |
|
2nω |
. (2.89) |
|
|
|
|
, |
|
|
|
|||
m |
(p2 −ω2 )2 + 4n2ω2 |
m |
(p2 −ω2 )2 + 4n2ω2 |
||||||
Поэтому общее решение уравнения вынужденных колебаний линейной системы при гармоническом возмущении с учетом (2.87), (2.89) запишется в виде
y= y0 + y = e−nt (C1 cos rt +C2 sin rt)+ M sin ωt + N cosωt.
2.7.Колебания независимой подвески13
Построить график вертикального смещения оси колеса легкового автомобиля массой mк = 30 кг, если для его крепления ис-
пользуется независимая рычажная подвеска со следующими характеристиками: коэффициент демпфирования амортизатора
k = 3 103 н сек/ м; жесткость пружины c =1,7 105 н/ м. Пред-
полагается, что внешняя сила, действующая на колесо, изменяются по закону:
P(t) = P0 + Pc cosωt, где P0 =850кг, Pс = 58кг, ω = 33 гц.
При этом P0 - постоянная (статическая) составляющая силы (реакция от дороги), а Pc cosωt - зависящая от времени динамиче-
ская составляющая нагрузки (обусловленная неровностями дороги).
В расчетах не учитывать упругость шины и инерционные характеристики подвески колеса.
Схематично независимая подвеска колеса показана на рис.I.12.
13 Общая задача о вертикальных колебаниях автомобиля и его агрегатов подробно рассмотрена Е.А.Лопаницыным (см. “Избранные проблемы прикладной механики и математики”. Сб. научных работ кафедры “Прикладная и вычислительная математика”, посвященный 80-летию чл.-корр. РАН Э.И.Григолюка. М.: МГТУ
“МАМИ”, 2003. 320 с.).

88
Пренебрегая вращательными движениями колеса вокруг оси подвески, будем учитывать только вертикальные перемещения колеса yк = yп . Массу подвески отнесëм к массе колеса.
Подвеска (рессора) моделируется линейно – упругим элементом (пружиной) жесткостью c, а амортизатор – демпфером с коэффициентом демпфирования k. Поэтому сила, действующая на колесо со стороны подвески, складывается из силы, пропор-
Рис. I.12
циональной перемещению (это сила упругости пружины cyп ) и
силы, пропорциональной скорости (силы демпфирования амортизатора: kdyп / dt). Следовательно, суммарное усилие, передаю-
щееся от подвески на колесо, будет равно
Fп = cyп + k dydtп .
Дифференциальное уравнение движения колеса под действием сил, действующих со стороны подвески и шины (см. рис. ), запишется в виде
mк d 2 yк = P(t)− Fп −mк g. dt2
Если масса колеса измеряется в кг, перемещение – в см, а силы P(t) и Fп - в кг, то уравнение приводится к виду
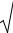
|
|
89 |
|
|
d 2 yк = g |
|
1 |
[P(t)− F |
] −1 , |
|
|
|||
dt2 |
|
п |
|
|
mк |
|
|
||
где g = 981см/ сек2.
Подставляя в для усилий P(t) и
d 2 yк dt2
это уравнение приведенные выше выражения Fп , получим
= g |
|
1 |
P + P cosωt −cy |
|
−k dyк |
−1 . |
||
|
|
к |
||||||
|
|
|
0 |
c |
|
|
||
|
mк |
|
|
|
dt |
|
||
После элементарных преобразований приходим к неоднородному линейному дифференциальному уравнению второго порядка:
d 2 y |
к +b |
dy |
к +b y |
к |
= b cosωt +b , |
||
dt2 |
|
||||||
1 |
dt |
2 |
3 |
4 |
|||
коэффициенты которого равны
kg |
|
cg |
|
|
Pc g |
|
|
|
P0 |
|
|
|
|
|
|
|
|
||||
b1 = m |
, |
b2 = m |
, |
b3 = |
, |
b4 |
|
|||
m |
= g m |
−1 . |
||||||||
к |
|
к |
|
|
к |
|
|
|
к |
|
Характеристическое уравнение для соответствующего однородного уравнения при заданных значениях параметров имеет комплексные сопряжëнные корни
k =α ± βi, где |
α = − |
b |
, β = |
|
|
b12 −4b2 |
|
. |
1 |
|
|
|
|||||
|
||||||||
|
|
|
||||||
12 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||
Частное решение неоднородного уравнения колебаний находится методом подбора.
В результате общее решение уравнения колебаний колеса запишется в виде
|
αt |
|
αt |
|
|
b3 |
2 |
|
|
yк (t) = C1e |
|
cos βt +C2e |
|
sin βt + |
|
|
|
[(b2 −ω |
)cosωt + |
|
|
(b ω)2 |
+(b |
−ω2)2 |
|||||
|
|
|
|
1 |
2 |
|
|
|
|
+b1ωsin ωt] +b2−1b4 .
Определяя далее произвольные постоянные C1 и C2 из начальных условий:
yк (0) = 0, yк′(0) = 0,
представим окончательно точное решение задачи в виде
yк (t) = a0 + a1 cosωt + a2 sin ωt +eαt (a3 cos βt + a4 sin βt),
