94

P = nπ 2.

EI l

Следовательно, чтобы стержень сохранял криволинейную форму равновесия, необходимо, чтобы сжимающая сила принимала значения

Число n =1,2,...в данной задаче имеет смысл числа полуволн си-

нусоиды (2.94), по которой происходит искривление оси стержня.

Из формулы (2.97) следует, что существует множество значений сжимающей силы P, при которых возможны различные искривлëнные формы равновесия продольно сжатого стержня. Наименьшее значение сжимающей силы, соответствующее n = 1,

называется критической (эйлеровой) силой и равно

P = π 2EI . l2

Пример. Найти собственные значения и собственные функции однородной краевой задачи для уравнения (2.90) при граничных условиях

Общее решение уравнения согласно (2.92) имеет вид y = C1 cos 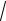λx +C2 sin λx.

Подставляя эти величины в граничные условия, после элементарных преобразований получим систему линейных однородных алгебраических уравнений относительно C1 и C2 :

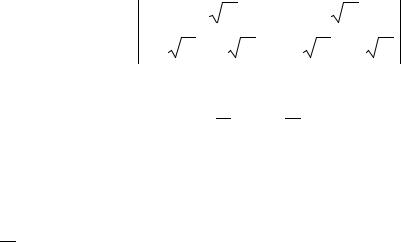
95

Ненулевое решение еë существует тогда и только тогда, к о- гда определитель системы равен нулю:

Раскрывая определитель, получим уравнение относительно параметра λ :

λ (cos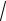λ −1) = 0,

корни которого являются собственными значениями задачи:

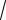λ = 2πn, n =1,2,..., в систему линейных однородных алгебраических уравнений относительно C1 и C2 , находим C2 = 0. Соот-

ветствующие собственные функции с точностью до множителя будут y = cos 2πnx.

2.9. Дифференциальные уравнения с переменными коэффициентами

Если коэффициенты ai (x), (i =1,2,...,n) линейного неоднородного уравнения

y(n) + a1 (x) y(n−1) + a2(x) y(n−2) + an−1 (x) y′+ an (x) y = f (x) (2.98)

и его правая часть f(x) представляют собой функции, которые определены и непрерывны на заданном интервале, то рассмотренные выше теоремы о структуре общего решения линейного неоднородного уравнения и соответствующего ему однородного уравнения остаются справедливыми. Остаются в силе также принцип суперпозиции решений для неоднородного уравнения и метод вариации произвольных постоянных. Но при этом нельзя искать фундаментальную систему решений однородного уравнения рассмотренным выше методом.

Одним из простейших линейных дифференциальных уравнений с переменными коэффициентами является уравнение Эйлера.

96

2.9.1. Уравнение Эйлера

Уравнением Эйлера называется линейное уравнение вида

xn y(n) + a1xn−1 y(n−1) + a2xn−2 y(n−2) + + an−1xy′+ an y = f (x). (2.100)

Как видно, уравнение Эйлера является уравнением с переменными коэффициентами специального вида, и оно приводится к уравнению с постоянными коэффициентами заменой независимой переменной x.

…………………………………

и подставляя (2.101) и (2.102) в (2.100), получим уравнение с постоянными коэффициентами относительно функции y(t).

В общем случае, для уравнения (2.99) формулы перехода (2.102) примут вид:

…………………………………..

Уравнение (2.103) есть уравнение Эйлера второго порядка. Применим замену независимой переменной и производных по формулам (2.101), (2.102). Тогда уравнение примет вид

и после упрощений получим линейное неоднородное уравнение с постоянными коэффициентами

Его общее решение

y = y0 + y1 + y2,

где y0 - общее решение соответствующего однородного уравнения:

y0 = C1e−t +C2 t e−t ,

y1 - частное решение неоднородного уравнения

y2 - частное решение неоднородного уравнения

Эти решения находятся методом подбора (см. выше) и имеют вид

y1 = 2, y2 = 0,25et .

Поэтому общее решение уравнения (2.104) будет

Теперь, чтобы от решения (2.105) перейти к общему решению исходного уравнения (2.103), возвращаемся к переменной x по формуле (2.101). В результате получим общее решение исходного уравнения (2.103) в виде

ческому уравнению относительно k.

Простому корню k1 характеристического уравнения соответствует частное решение xk1 , а m-кратному действительному

Если коэффициенты дифференциального уравнения действительны, а характеристическое уравнение имеет комплексные сопряженные корни кратности m, то уравнение Эйлера будет иметь 2m частных линейно независимых решений вида:

В общем случае решения уравнения с переменными коэффициентами (2.98) строятся приближёнными методами. Одним из эффективных приближённых методов является метод степенных рядов [5,9,10].

Рассмотрим два варианта применения этого метода:

1)метод степенных рядов в форме метода неопределённых коэффициентов;

2)разложение решения задачи Коши в степенной ряд с помощью формулы Тейлора16.

16Т е й л о р Брук (18.08.1685 – 29.12.1731) – английский математик.