47

сле разделения переменных к интегралу ∫(y4 +C1 )−1/ 2 dy от так

называемого дифференциального бинома [15], который в данном случае вообще не выражается через элементарные функции.

В качестве практического примера применения метода понижения порядка рассмотрим задачу об осесимметричном изгибе упругих круговых пластин.

2.1.1. Осесимметричный изгиб круговой пластины

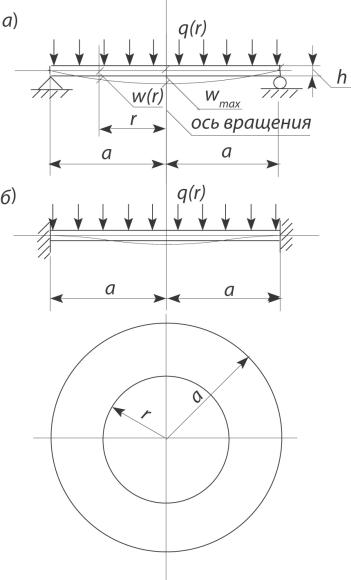
Пусть тонкая упругая круговая пластина радиуса a и толщиной h нагружена внешним равномерно распределëнным давлением (рис. I.6). Случай а) соответствует свободному опиранию на внешнем контуре, случай б) – жëсткому защемлению.

Рис. I.6

48

Как известно, дифференциальное уравнение осесимметричного изгиба тонкой упругой круговой пластины может быть записано в виде [17, 21]

где

w-прогиб пластины, r - текущий радиус, q - интенсивность внеш-

гости и коэффициент Пуассона8 материала пластины). Уравнение (2.32) представляет собой неоднородное линей-

ное дифференциальное уравнение 4-го порядка с переменными коэффициентами и может быть проинтегрировано методом понижения порядка.

Действительно, последовательно интегрируя уравнение

8 П у а с с о н Симеон Дени (21.06.1781 – 25.04.1840) – французский математик, механик и физик.

чательное выражение для общего решения в принятой в теории пластин форме

слагаемое в формуле (2.33), представляющее собой частное решение неоднородного уравнения (2.32), приводится к виду

Dq ∫drr ∫rdr∫drr ∫rdr = Dq ∫drr ∫rdr∫2r dr = Dq ∫drr ∫r43 dr =

Окончательно прогиб круговой пластины, нагруженной равномерно распределëнным поперечным давлением, будет равен

Можно показать, что внутренние силовые факторы: радиальный изгибающий момент M r и поперечная сила Qr выражают-

ся через прогиб по формулам [17, 21]:

50

С учетом (2.34) выражения (2.35) приводятся к виду

Ещë два условия для определения произвольных постоянных следуют из рассмотрения условий в центре пластины (при

r = 0).

Во-первых, из условия ограниченности прогиба в центре необходимо принять

(так как при r → 0 ln r неограниченно возрастает, а прогиб w r=0

должен быть конечной величиной).

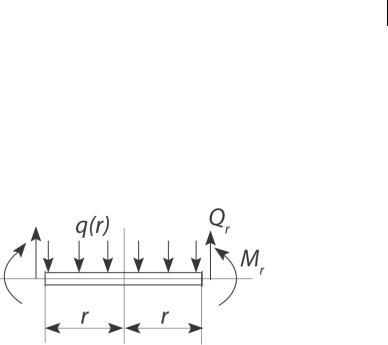
Во-вторых, выделяя из пластинки круг малого радиуса r и заменяя действие отброшенной части внутренними силовыми факторами – изгибающим моментом и поперечной силой, равномерно распределëнными по контуру сечения, из условия равновесия выделенной части пластины (см. рис. I.7) получим формулу для Qr :

Приравнивая выражения (2.36) и (2.39), находим

51

С учетом (2.38), (2.40) выражения (2.34) и (2.36) примут вид

Теперь из граничных условий на внешнем контуре пластины получим систему уравнений для определения постоянных интегрирования C1 и C2 :

а его максимальное значение в центре пластины (при r = 0) равно

Б) Для жестко защемлëнной по внешнему контуру круговой пластины условия в центре, очевидно, будут такими же, как и для свободно опëртой пластины, а на внешнем контуре должны быть равны нулю прогиб и угол поворота сечения:

52

из которой находим

В результате зависимость прогиба защемлëнной пластины от радиуса будет определяться выражением

а максимальное значение прогиба в центре пластины будет равно

2.2. Линейные однородные дифференциальные уравнения n-го порядка. Общие свойства решений

Линейным дифференциальным уравнением n - го порядка называется уравнение

y(n) + a1 (x)y(n−1) + a2(x)y(n−2) + + an−1 (x)y′+ an (x)y = f (x), (2.41)

содержащее неизвестную функцию и все её производные до n-го порядка включительно в первой степени. Если все коэффициенты уравнения постоянны: ai = const (i =1,2,...,n), то оно называется

линейным дифференциальным уравнением с постоянными коэффициентами. Если хотя бы один из коэффициентов ai является

функцией от x, то уравнение (2.41) будет уравнением с переменными коэффициентами.

Если правая часть уравнения f (x) ≡ 0, то уравнение (2.41) принимает вид

y(n) + a1 y(n−1) + a2 y(n−2) + + an−1 y′+ an y = 0,

и называется линейным однородным дифференциальным уравнением, в противном случае – линейным неоднородным.

Левая часть уравнения (2.41) называется линейным диф-

ференциальным оператором и обозначается через

53

С учетом обозначения (2.42) линейное однородное дифференциальное уравнение n - го порядка может быть записано в компактной форме:

Свойства оператора Ln (y).

1. Ln (Cy) = CLn (y), где C – некоторое число. Это свойство назы-

вают свойством однородности оператора.

2. Ln (y1 + y2) = Ln (y1 )+ Ln (y2) - это свойство называют свойством

аддитивности оператора.

ной комбинации функций, равен линейной комбинации операторов, взятых от этих функций (напомним, что линейной комбинацией функций называется сумма произведений функций на различные постоянные числа, то есть выражение вида С1 y1 +C2 y2 + +Cn yn ).

Используя свойства оператора Ln (y), легко показать, что

справедливы следующие свойства решений линейного однородного дифференциального уравнения:

1. Если функция y(x) является решением линейного однородного дифференциального уравнения Ln (y) = 0, то функция Cy(x), где C – произвольная постоянная, также является решением этого уравнения.

2.Если функции y1 (x) и y2(x) являются решениями линейного однородного дифференциального уравнения Ln (y) = 0, то сум-

ма функций y1 (x)+ y2(x) также является решением этого уравнения.

3.Если y1 (x), y2(x), , ym (x)- какие либо частные решения урав-

нения Ln (y) = 0, то любая их линейная комбинация с произ-

m

вольными коэффициентами ∑Ci yi также будет решением

i=1

этого уравнения.

54

Действительно, на основании свойств однородности и аддитивности линейного дифференциального оператора можно записать:

+C2Ln (y2)+...+Cm Ln (ym ).

Так как функции y1 (x), y2(x), , ym (x) являются частными решениями уравнения Ln (y) = 0, то все слагаемые в правой части

m

довательно, ∑Ci yi также является решением уравнения.

i=1

Последнее свойство называется принципом суперпозиции (наложения) решений линейных однородных дифференциальных уравнений n - го порядка.

Заметим также, что линейное однородное дифференциальное уравнение Ln (y) = 0 всегда имеет тривиальное решение

y ≡ 0.

В теории линейных дифференциальных уравнений важную роль играют понятия линейной независимости и линейной зависимости функций.

Пусть имеется система функций y1 (x), y2(x), , yn (x), определëнных на некотором интервале (a,b), и пусть C1, C2, , Cn - различные действительные числа.

Система функций называется линейно независимой, если линейная комбинация этих функций С1 y1 +C2 y2 + +Cn yn = 0

тогда и только тогда, когда все коэффициенты линейной комбинации C1 = C2 =...= Cn = 0. В противном случае система функций

линейно зависима.

Если система функций линейно зависима, то по крайней мере одна из них является линейной комбинацией других. Если,

например, C1 ≠ 0, то из условия С1 y1 +C2 y2 + +Cn yn = 0 следует