Пример. Решить методом Эйлера систему

Пример. Решить методом Эйлера систему

Характеристическое уравнение системы

Этот метод применим к решению систем неоднородных линейных уравнений n-го порядка. Ограничимся для простоты нормальной системой двух линейных уравнений с постоянными коэффициентами

Пусть общее решение однородной системы уравнений известно:

Интегрируя эти уравнения, получим

Характеристическое уравнение системы

Общее решение однородной системы (3.18) запишется в виде

Пусть общее решение однородной системы уравнений известно:

Пример. Решить систему

Принимаем частное решение системы (3.31) в виде

Интегрируя эти уравнения, получим

Общее решение системы запишется в виде:

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный машиностроительный университет "МАМИ"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

диф 1.pdf

Скачиваний:

121

Добавлен:

05.06.2015

Размер:

2.19 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 1917 18 19 > Следующая >>>

				113
	y (x)			y (x)		y	(x)
	11			12		1n
	y21(x)			y22 (x)		y2n (x)
Y1			Y 2
Y1	(x) = .	,	Y 2	(x) = .		, ,Y n (x) = .
	.			.		.
	.			.		.

	yn1 (x)			yn 2	(x)	yn n		(x)

образуют фундаментальную систему решений этой системы. Следовательно, общее решение однородной системы диф-

ференциальных уравнений запишется в виде

Y (x)=C1 Y1 (x)+C 2Y 2(x)+…+C n Y n (x)

или

y1 (x) = C1 y11 (x) + C2 y12 (x) + + Cn y1n (x),

y2(x) = C1 y21(x)+C2 y22(x)+ +Cn y2n (x),

…………………………………………….

yn (x) = C1 yn1 (x) + C2 yn 2 (x) + + Cn yn n (x),

где C1, C2,…,Cn

- произвольные постоянные.

y′

= −4 y

+ y

(3.18)

Принимаем

y2′ = −2y1 − y2.

y =α

e k x,

=α

e k x

(3.19)

Подставляя (3.19)

в (3.18),

получим систему

(−4 − k)α1

+α2 = 0,

(3.20)

+ (−1 − k)α2 = 0.

− 2α1

− 4 − k

= 0.

− 2

−1 − k

Следовательно,

(−4 −k)(−1−k)+2 = 0

или

k 2

+ 5k + 6 = 0.

Корни уравнения k1 = −2, k2 = −3 - действительны и различны.

										114
Подставляя k1		= −2 в (3.20), получим
							− 2α1 +α2												= 0,				(3.21)
								2α1 +α2											= 0.				(3.21)
							−	2α1 +α2											= 0.
Система (3.21) совместная,																но			неопределённая.				Полагая
α1 =α11 =1, находим α2					=α21			= 2.							Поэтому
			y				= e−2x ,								y		21		= 2e−2x .				(3.22)
				11													21
Подставляем теперь в систему (3.20)																		k2 = −3. Получим
							−α		1		+α					2		= 0,					(3.23)
									1							2							(3.23)
							−	2α1 + 2α2 = 0.
Решение этой системы принимаем в виде α1 =α12																				=1, α2			=α22 =1.
При этом			y				= e−3 x ,									y			=e−3 x .
			y				= e−3 x ,									y		22	=e−3 x .				(3.24)
				12														22
Общее решение однородной системы (3.18) запишется в виде
y		(x) = C y			(x)+C					2		y		(x)					= С e−2x +C		e−3 x ,
1		1	11							2		12							1	2
y	2	(x) = C y		21		(x)+C					2	y	22			(x) = 2С e−2x +C						e−3 x .	(3.25)
	2	1		21							2		22						1		2

3.3. Метод вариации произвольных постоянных

y10	= C1 y11	+C2 y12	,	(3.27)
y20 = C1 y21 +C2 y22,				(3.27)
y20 = C1 y21 +C2 y22,

где С1 , C2 - произвольные постоянные, а y11 , y21, y12 , y22 - част-

ные решения однородной системы, соответствующие различным корням характеристического уравнения.

115

В соответствии с методом вариации частное решение неоднородной системы отыскивается в форме, аналогичной по структуре общему решению однородной системы, но произвольные постоянные в ( 3.27) заменяются неизвестными функциями, то есть принимается

y1 = C1 (x) y11 + C2 (x) y12,
y2 = C1 (x) y21 + C2 (x) y22.	(3.28)

Подстановка (3.28) в ( 3.26) приводит к следующей системе двух дифференциальных уравнений первого порядка относитель-

но производных от неизвестных функций						C1 (x), C2 (x):
	C′(x)		y	+C′	(x) y	=		f	(x),		(3.29)
		1	11	2	12			1
	C1′(x) y21 + C2′(x) y22 = f2 (x).
Разрешая систему (3.29) по формулам Крамера, получим
два дифференциальных уравнения первого порядка
С1′(x) =	f1 y22	− f2 y12		, С2′(x) =				f2 y11 − f1 y21		.	(3.30)
	y11 y22	− y12 y21
							y11 y22 − y12 y21

Интегрируя эти уравнения, находим варьируемые функции С1 (x), C2 (x) и подставляем их в (3.28). Общее решение системы

(3.26) запишется в виде

y1 = y10 + y1 ,

y2 = y20 + y2.

Пример. Решить систему
y′ = −4 y		+ y		+ x,	(3.31)
1	1		2		(3.31)
y′ = −2y1 − y2 + 3x.
Общее решение однородной системы, согласно					(3.25),
имеет вид

y10 = C1 y11 +C2 y12 = С1 e−2x +C2 e−3x ,

y	20	= C y			21	+C	2	y	22	= 2С e−2x +C					2	e−3x .	(3.32)
	20		1		21		2		22		1				2
Принимаем частное решение системы (3.31) в виде
		y		= C (x)e−2x + C							2	(x)e−3 x ,
			1			1					2
		y	2	= 2C (x)e−2x + C									2	(x)e−3 x .			(3.33)
			2			1							2

116

Подставляя (3.33) в ( 3.31), получим после элементарных преобразований

C1′(x)e−2x + C2′(x)e−3 x = x,2C1′(x)e−2x + C2′(x)e−3 x = 3x.

Решение этой системы приводит к дифференциальным уравнениям первого порядка с разделяющимися переменными:

e−3x

e−2x

C1′(x) =

3x e−3x

= 2xe2x ,

C2′(x) =

2e−2x

= −xe3x .

e−2x

e−3x

e−2x

e−3x

2e−2x e−3x

				С1 (x)				= 2∫xe				2x			dx	= e		2x						−		1
				С1 (x)				= 2∫xe							dx	= e					x			−		2		,
																										2
				С2 (x)				= −∫xe					3 x		dx	=	e3 x						1		− x
				С2 (x)				= −∫xe							dx	=		3					3		− x				.
Поэтому																		3					3
Поэтому
y1 = C1 (x)e				−2x			+ C2 (x)e				−3 x			= x −			1			+		1		1			− x					=		2x
y1 = C1 (x)e							+ C2 (x)e							= x −			2			+		3			3		− x					=			3
																	2					3			3										3
y2 = 2C1 (x)e			−2x			+ C2 (x)e				−3 x										1				+		1			1						=
y2 = 2C1 (x)e						+ C2 (x)e								= 2 x −						2				+		3			3	− x					=
																				2						3			3
Общее решение системы запишется в виде:
y		= y					+ y		= C e−2x +C										e−3 x					+ 2x −							7		,
y		= y					+ y		= C e−2x +C										e−3 x					+ 2x −									,
	1				10			1			1						2									3				18
																										3				18
y	2	= y			20		+ y	2	= 2C e−2x +C											2	e−3 x + 5x − 8.
	2				20			2				1								2									3			9
																													3			9

−187 , 53x − 89.

3.4. Задача о свободных вертикальных колебаниях автомобиля

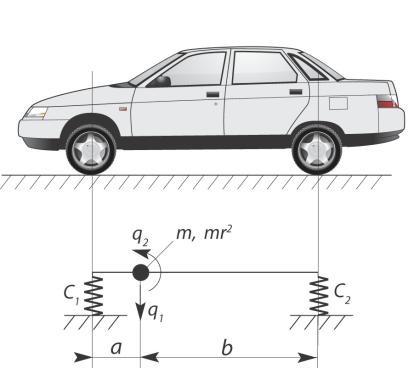
Эта задача подробно рассмотрена в [18]. Динамическая схема автомобиля показана на рис. I.15.

117

Рис. I.15

Будем предполагать, что вертикальные колебания автомобиля происходят параллельно его плоскости симметрии, деформациями кузова по сравнению с осадками опор можно пренебречь, поэтому на динамической схеме автомобиля горизонтальный стержень, моделирующий кузов автомобиля, можно считать абсолютно жестким.

Введëм следующие обозначения: m- масса кузова,

C1,C2 - приведëнные жесткости передней и задней подвесок автомобиля,

I p = mr 2 - момент инерции кузова относительно поперечной оси,

проходящей через центр тяжести (r - радиус инерции),

a,b - расстояния от передней и задней опор до центра тяжести, q1 - вертикальное перемещение центра тяжести (q1 > 0, если на-

правлено вниз),

q2 - угол поворота стержня относительно центра тяжести (q2 > 0,

если поворот происходит против хода часовой стрелки). Рассматриваемая система обладает двумя степенями свобо-

ды.

118

Так как осадки упругих опор равны

q1 + aq2

(для передней

опоры) и

q1 −bq2 (для задней опоры), то кинетическая и потен-

циальная энергия системы равны

П =

C (q + aq

(q −bq

1 1

∂T

Так как

= m

dq1

dt2

∂

∂T

= I

dq2

p dt2

∂q

∂

∂П

= C

(q + aq

)

(q −bq

= C a(q + aq

)−C

b(q −bq

∂q

то уравнения Лагранжа относительно обобщëнных координат

и q2 [22]

∂T

∂П

(i =1,2)

−

= − ∂

∂

примут вид:

m d 2q1					+(C	+C	)q +(C a −C				b)q	2		=
		dt	2		1	2		1	1	2		2
		dt
		d 2q2
I	p	d 2q2			+(C a −C			b)q	+(C a2	+C			b2
	p	dt		2		1	2	1	1		2
		dt

(3.34)

)q2 = 0.

В результате приходим к системе двух обыкновенных линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами.

Будем искать частные решения этой системы в виде

q1 = A1 sin(pt +ϕ),

q2 = A2 sin(pt +ϕ).

(3.35)

Тогда подставляя (3.35) в (3.34), получим систему линейных однородных алгебраических уравнений относительно амплитуд A1 и A2 :

119

(C		+C	2	−mp2 )A +(C a −C					b)A = 0,
	1		2			1	1	2			2		(3.36)
					b)A +(C a2		+C	b2 − I			p2 )A	= 0.	(3.36)
(C a −C					b)A +(C a2		+C	b2 − I		p	p2 )A	= 0.
	1			2	1	1	2			p	2
Система (3.36) имеет тривиальное решение												A1 = A2 = 0, ко-

торое соответствует отсутствию колебаний и реализуется только при однородных начальных условиях

q1 = q2 = dqdt1 = dqdt2 = 0.

Это решение, очевидно, не представляет физического инте-

реса.

Ненулевые (нетривиальные) решения системы (3.36) существуют при условии равенства нулю определителя системы

C +C

−mp2

C a −C

= 0.

(3.37)

C a −C

C a2

b2 − I

Раскрывая этот определитель, получим частотное уравне-

ние:

(a +b)2

C a2

C C

(3.38)

−

+ 1

1 2

= 0.

I p

mI p

Каждому из его корней соответствует определëнное соо т- ношение между амплитудами, определяющее собственную форму колебаний. Это соотношение можно найти из любого из уравнений системы (3.36), например, из первого

	A	=	mp2 −(C			+C			)	.	(3.39)
	2		1					2
	A		1				b	2
	A		C a −C				b
1			1			2
Рассмотрим различные частные случаи.
1) Первый частный случай.
Пусть			r =
					,						(3.40)
				ab	,						(3.40)

то есть радиус инерции равен среднему геометрическому величин a и b. Это соотношение реализуется, если расстояние a +b между осями колес заметно меньше общей длины автомобиля.

При выполнении условия (3.40) частотное уравнение (3,38) принимает вид

			120
	p4 − (C1a +C2b)(a +b) p2			+ C1C2(a +b)2 = 0.			(3.41)
	mab				m2ab
Дискриминант этого биквадратного уравнения равен
D =	(C1a +C2b)2(a +b)2	−	4C1C2(a +b)2		=	(a +b)2(C1a −C2b)2		.

	(mab)2		m2ab			(mab)2

Следовательно, уравнение (3.41) будет иметь действительные и различные корни

p2	=	C1 (a +b)	,	p2	=	C2(a +b)	.	(3.42)


1		mb		2		ma

Подставляя эти корни поочередно в соотношение (3.39), получим:

- для первой формы колебаний (при p2 = p2 )
				C1 (a +b)		1
	A21		m	C1 (a +b)	−(C +C		)		1 .
			m	mb	−(C +C		)
		=		mb		1 2		=		(3.43)
	A	=		C a −C		b		=		(3.43)
	A			C a −C		b			b
11			1		2

Здесь вторые индексы обозначают номер рассматриваемой собственной формы;

- для второй формы колебаний (при p2						= p22 )
	A22		m C1 (a +b)	−(C +C			)		1 .
	A22	=	ma			1 2		= −		(3.44)
	A	=	C a −C		b			= −		(3.44)
	A		C a −C		b				a
12			1	2

Эти формы показаны на рис. 1.16.

Из соотношений (3.43), (3.44) следует, что A11 = bA21 - вертикальное перемещение сосредоточенной массы при том, что пра-

вая пружина недеформирована, а A21- угол поворота стержня; при

колебаниях по второй форме недеформирована левая пружина, из (3.44) следует A12 = −aA22, поэтомуA22 теперь угловое перемеще-

ние стержня.

Таким образом, особенностью рассматриваемых форм колебаний является неподвижность одной подвески автомобиля при колебаниях другой подвески. Практически это означает, что подвески автомобиля являются независимыми, то есть колебания одной подвески не передаются другой. При этом свободные коле-

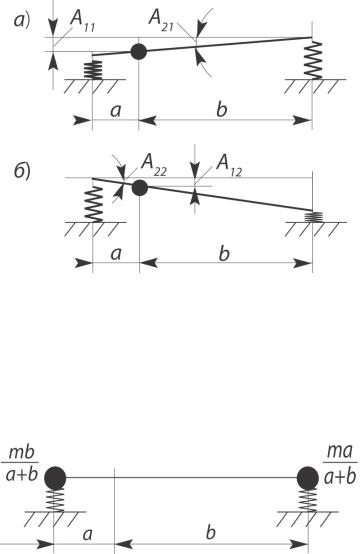
121

бания каждой из подвесок характеризуются различными частотами.

Рис. I.16

Свойства такой системы наглядно изображаются схемой, показанной на рис. I.17 (здесь масса m распределяется обратно пропорционально расстояниям от центра масс автомобиля, а моменты масс относительно центра тяжести одинаковы).

Рис. I.17
2) Второй частный случай:
C1a = C2b.	(3.45)

Тогда уравнения (3.36) разделяются и принимают вид

A (C +C			2	−mp2) = 0,					(3.46)
1	1		2
A (C a2		+C			b2	− I	p	p2) = 0.	(3.47)
2	1			2			p

Независимость уравнений (3.46) и (3.47) означает, что при соблюдении условия (3.45) могут происходить чисто вертикальные колебания без поворотов (подпрыгивание) (рис. I.18а) или чисто угловые колебания при неподвижном центре тяжести (га-

лопирование) (рис I.18б).

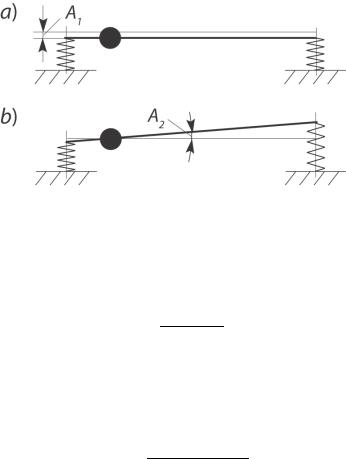
122

Рис. I.18

В первом случае (подпрыгивание без поворотов) имеем A1 ≠ 0, A2 = 0. Тогда из (3.46) следует C1 +C2 −mp2 = 0.

Поэтому квадрат первой частоты будет равен p2 = p12 = C1 m+C2 .

Во втором случае (угловые колебания при неподвижном центре тяжести) A1 = 0, A2 ≠ 0. Поэтому из уравнения (3.47) сле-

дует выражение для квадрата второй частоты p2 = p22 = C1a2 I+p C2b2 .

Таким образом, частоты подпрыгивания и галопирования различны. Формы таких колебаний показаны на рис. I.18.

3) Случай равенства обеих частот.

Частотное уравнение (3.38) будет иметь равные корни, если его дискриминант равен нулю. Это приводит к следующему условию:

					2			2	2			2
				C1a	2	+C2b		2			4C1C2(a +b)
C +C		2	+	C1a		+C2b				−	4C1C2(a +b)		= 0.	(3.48)
C +C			+							−			= 0.	(3.48)
	1					r	2				r	2
						r					r

Легко убедиться в том, что условие (3.48) выполняется, если одновременно выполняются условия (3.40) и (3.45).

Итак, если параметры динамической схемы автомобиля удовлетворяют условиям (3.40) и ( 3.45), то единственная собственная частота колебаний будет определяться формулой

p2	= p2	= 1		+C2 + C1a	2	+C2b		2			= C1 +C2 ,
p2	= p2	= 1	C1	+C2 + C1a		+C2b					= C1 +C2 ,
1	2	2		m	mr		2		r2		m
		2		m	mr				r2	=ab	m
									C a=C		b
								1		2

	123
следовательно,
p =		C1 +C2	.
p =			.
		m

Заметим, что схема автомобиля, у которого частоты p1 и p2

равны, считается более рациональной с точки зрения комфортности езды, так как в этом случае сильные колебания возникают лишь при некоторой единственной частоте толчков, тогда как в случае p1 ≠ p2 сильные колебания могут происходить при двух

разных значениях частот.

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1617 / 1917 18 19 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.09.20193.2 Mб2Диплом Н.Бакаевой.doc
#
05.06.2015344.58 Кб26диплом на 5.doc
#
19.09.2019364.03 Кб3ДИПЛОМ оконч.doc
#
31.07.20194.12 Mб60дипломная работа Алексея Симакова.docx
#
23.11.201928.11 Кб5Дискретная матетатика.docx
#
05.06.20152.19 Mб121диф 1.pdf
#
22.09.201986.53 Кб1ДМИТРИЕВ !.doc
#
27.03.2016342.37 Кб62Дневник по производственной практике(ПОО) для студентов 08.03.01, 08.05.01.pdf
#
27.09.201974.75 Кб1Дневник, отчет, отзыв.doc
#
27.03.201614.85 Кб22Добровольная сертификация продукции.docx
#
05.06.201526.63 Кб20док.docx

= a21y1 + a22 y2 + f2 (x).

= a21y1 + a22 y2 + f2 (x).