70

Приравнивая коэффициенты в обеих частях получившегося тригонометрического равенства при cos 2x и sin 2x , приходим к

системе

−4A −4B = 0,

4A −4B = 3,

а общее решение запишется в виде

Характеристическое уравнение k 2 − 2k + 4 = 0 имеет комплексные сопряжëнные корни: k1 =1 + 3i , k2 =1 − 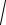3i . Поэтому част-

ные линейно независимые решения уравнения (2.58) будут (см. таблицу 1, случай 2a)

а общее решение однородного уравнения запишется в виде

y0 = ex (C1 cos 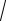3x + C2 sin 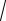3x).

2). Находим частное решение неоднородного уравнения методом подбора. Сравниваем правую часть f (x) = (x + 2)e3 x c общим выражением (1) из таблицы 2: f (x) = Pn (x)eα x . Очевидно, что в данном случае n=1, α = 3. Так как α ≠ k j (j=1,2), то m = 0.

Поэтому принимаем (см. таблицу 2, случай 1А):

y = R1 (x)e3x = (Ax + B)e3x ,

где A и B - неопределëнные коэффициенты. Находим их, используя стандартную процедуру:

71

4y = (A x + B) e3 x ,

−2 y′ = (3A x + A +3B )e3 x , 1 y′′ = (9A x +6A +9B)e3 x .

y′′− 2y′ + 4 y = (7A x + 4A + 7B)e3 x = (x + 2)e3 x .

Сокращая на e3 x и приравнивая коэффициенты при одинаковых степенях x, получаем:

Общее решение уравнения:

Соответствующее ему характеристическое уравнение k 2 + 4 = 0 имеет мнимые корни k1,2 =± 2i . Поэтому частные решения урав-

нения будут (см. таблицу 1, случай 2б) y1 = cos 2x, y2 = sin 2x . Общее решение примет вид: y0 = C1 cos 2x + C2 sin 2x.

2). Находим сначала частное решение неоднородного уравнения y′′+ 4 y = 5sin 2x.

Сравнивая f1 (x) = 5sin 2x с выражением (см. таблицу 2, случай 2) f (x) = M cos β x + N sin β x , определяем β = 2.

Сравниваем β i = 2i с корнями k1,2. Так как β i = k1 = 2i, то m =1. Поэтому принимаем y1 = x(Acos 2x + Bsin 2x).

Тогда

y1′′ +4 y1 = −4Asin 2x +4B cos 2x = 5sin 2x.

Приравнивая коэффициенты при sin 2x и cos 2x, получим A = -5/4, B = 0. Следовательно,

y1 = −54 xcos 2x.

3). Далее находим частное решение уравнения y′′ + 4 y = −cos x.

Сначала находим общее решение заданного линейного неоднородного дифференциального уравнения второго порядка.

торое имеет два одинаковых действительных корня: k1 = k2 = 3.

Поэтому общее решение однородного дифференциального уравнения запишется в виде

y0 = C1e3x + C2xe3x .

73

Частное решение неоднородного дифференциального уравнения находим методом подбора, принимая (см таблицу 2, случай

3А):

Поэтому общее решение исходного дифференциального уравнения примет вид:

y = e3x (C1 +C2x)− 12e2x (cosx +sin x).

Далее находим произвольные постоянные из граничных условий.

В результате решение краевой задачи запишется в виде:

74

щее решение однородного уравнения будет иметь вид:

y0 = C1 +C2e−x .

Сравнивая правую часть уравнения f (x) = x cos 2x с общим выражением, при котором применим метод подбора (случай 3 из таблицы 2): f (x) = P(x)eax cos βx +Q(x)eax sin βx, находим n = 0,

α = 0, β = 2. Так как число α + βi = 2i не совпадает с корнями характе-

ристического уравнения, то m = 0. Следовательно, частное решение ищем в виде

y = Rn (x)eα x cos βx +Tn (x)eα x sin βx.

Подставляя найденные значения n,α,β , получим

y = (Ax + B)cos 2x +(Cx + D)sin 2x.

Подставляем это решение в уравнение

y = (Ax + B)cos 2x +(Cx + D)sin 2x.

y′ = (2Cx + A + 2D)cos 2x +(−2Ax −2B +C)sin 2x,

y′′ = (−4Ax −4B + 4C)cos 2x +(−4Cx −4A −4D)sin 2x .

Поэтому

y′′+ y′ = (−4Ax −4B + 4C)cos 2x +(−4Cx −4A −4D)sin 2x +

+(2Cx + A + 2D)cos 2x +(−2Ax −2B +C)sin 2x = x cos 2x.

После приведения подобных членов получим

[(−4A + 2C)x + A −4B + 4C + 2D]cos 2x +[−(2A + 4C)x −4A −2B −

−4D +C]sin 2x = x cos 2x.

Приравниваем сначала коэффициенты в левой и правой частях последнего равенства при cos 2x и sin 2x :

−4A + 2C)x + A −4B + 4C + 2D = x,

−(2A + 4C)x −4A −2B −4D +C = 0.

Приравнивая теперь коэффициенты при одинаковых степенях x в левой и правой частях полученных равенств, получим систему 4- х алгебраических уравнений относительно неопределëнных к о- эффициентов: