
tjurin_teorija_verojatn_978-5-94057-540-5_1
.pdf§ 2. Распределение Пуассона |
151 |
|
|
Суммирование этого ряда можно начинать со значения m =1, так как при m =0 слагаемое mp(m, λ) равно 0. Поэтому
∞ |
λm |
∞ |
λm−1 |
|
EX = e−λ mX=1 m m! |
= λe−λ mX=1 |
|
. |
|
(m −1)! |
||||
Введем новый индекс суммирования k, положив k =m −1. Тогда согласно соотношению (2.1.2) получаем
EX = λe−λ X∞ λk = λe−λeλ = λ·1 = λ. k!
k=0
По определению дисперсии DX =EX2 −(EX)2. Так как EX нам уже известно, осталось вычислить EX2 . Проще вычислить EX( X −1), что мы и сделаем ниже. Если же мы будем знать EX( X −1), то будем знать и EX2 , так как
EX( X −1) = EX2 −EX.
Итак, вычисляем:
X∞
EX( X −1) = m(m −1) p(m, λ).
m=0
Здесь обращаются в 0 два первых слагаемых (при m =0 и m =1), а потому суммирование можно начинать со значения m =2. Поэтому
|
∞ |
∞ |
||
|
λm |
= λ2 e−λ mX=2 |
λm−2 |
|
EX( X −1) |
= e−λ mX=2 m(m −1) m! |
|
. |
|
(m −2)! |
||||
Введем новый индекс суммирования k, положив k =m −2. Тогда
EX( X −1) = λ2 e−λ X∞ λk = λ2 . k!
k=0
Поскольку DX =EX( X −1) +EX −(EX)2, получим, что
DX = EX( X −1) +EX −(EX)2 = λ2 +λ−λ2 = λ.
Упражнения
1. Случайная величина X имеет распределение Пуассона с пара-
метром λ=1. Вычислите P5 mP( X =m) (т. е. часть суммы, составля-
m=0
ющей математическое ожидание случайной величины X). Велико ли различие между полученной величиной и EX?
2. Случайная величина X имеет распределение Пуассона с параметром λ. Вычислите EX( X −1)( X −2).

152 Глава 3. Некоторые важные распределения вероятностей
Распределение суммы независимых случайных величин, распределенных по Пуассону. Распределение вероятностей суммы независимых случайных величин отличается от распределений суммируемых величин. При этом, как правило, изменяется сам тип распределения суммируемых величин. Так, если рассмотреть в качестве случайной величины число очков, выпадающих на одной правильной игральной кости, то все возможные значения этой величины равновероятны. Однако распределение суммы двух таких независимых случайных величин, т. е. распределение суммы очков, выпавших при двух бросках игральной кости, уже не является равномерным. Одни значения суммы имеют меньшие вероятности, а другие — большие. (Распределение суммы числа очков, выпавших при двух бросках игральной кости, приведено в п. 1.2 гл. 2.)
Во многих практических задачах, связанных с распределением Пуассона, приходится рассматривать суммы независимых случайных величин, распределенных по Пуассону. Оказывается, что сумма независимых случайных величин, распределенных по Пуассону, тоже распределена по Пуассону.
Теорема 2.1.1. Пусть случайные величины X1 и X2 распределены по Пуассону с параметрами λ1 и λ2 соответственно. Тогда случайная величина X1 + X2 распределена по Пуассону с параметром λ1 +λ2.
Доказательство. Ясно, что сумма X1 + X2 может принимать только целые неотрицательные значения, потому что таковы и ее слагаемые X1 и X2 . Поэтому, чтобы узнать распределение величины X1 + X2, надо вычислить P( X1 + X2 =m) для каждого m =0, 1, … Складывая целые неотрицательные числа, в результате можно получить m только одним из перечисленных ниже способов:
m = 0 +m = 1 +(m −1) = … = (m −1) +1 = m +0.
Поэтому событие ( X1 + X2 =m) есть сумма непересекающихся собы-
тий вида ( X1 =k, X2 =m −k), где k =0, 1, …, m. Следовательно,
P( X1 + X2 = m) = P( X1 = 0, X2 = m) +P( X1 = 1, X2 = m −1) +… |
|
… +P( X1 = m, X2 = 0). |
(2.1.5) |
Поскольку случайные величины X1 и X2 независимы, независимы |
|
и события ( X1 =k) и ( X2 =m −k), а потому |
|
P( X1 = k, X2 = m −k) = P( X1 = k)P( X2 = m −k). |
(2.1.6) |

§ 2. Распределение Пуассона |
153 |
|
|
Вспомним теперь, что случайные величины X1 и X2 распределены по Пуассону, а потому
|
λk |
|
|
|
λm−k |
|
|||
P( X1 = k) = e−λ1 |
1 |
, |
P( X2 |
= m −k) = e−λ2 |
|
2 |
|
. |
(2.1.7) |
k! |
(m |
− |
k)! |
||||||
|
|
|
|
|
|
|
|
|
|
Соединив соотношения (2.1.5), (2.1.6) и (2.1.7), получим, что для m =0, 1, … справедливо равенство
|
|
|
m |
λk |
|
λm−k |
|
||
P( X1 + X2 = m) = e−(λ1 |
+ |
λ2 ) |
Xk=0 |
1 |
|
|
2 |
. |
(2.1.8) |
|
k! (m |
−k)! |
|||||||
Домножим (и разделим) каждое слагаемое под знаком суммы в фор-
муле (2.1.8) на один и тот же множитель |
|
m! |
|
. Тогда |
|
|||||||||||||
(λ1 +λ2 ) |
m |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
(λ |
|
+ |
λ |
) |
m m |
|
m! |
|
|
k |
λ |
m−k |
|
||
P( X1 + X2 = m) = e−(λ1 |
+ |
λ2 ) |
1 |
|
|
Xk=0 |
|
|
|
λ |
|
|
|
|||||
|
|
2 |
|
|
|
|
|
1 2 |
. |
(2.1.9) |
||||||||
|
|
|
m! |
|
|
k!(m −k)! |
(λ1 +λ2 )m |
|||||||||||
Присмотревшись к сумме, участвующей в соотношении (2.1.9), замечаем, что она (по формуле бинома) равна
|
λ |
|
λ |
|
m |
1 |
+ |
2 |
= 1. |
||
λ1 +λ2 |
λ1 +λ2 |
Следовательно, для всякого m =0, 1, … справедливо равенство
P( X1 + X2 = m) = e−(λ1 +λ2 ) (λ1 +λ2 )m , m!
что и требовалось доказать.
Следствие. Пусть случайные величины X1, X2, …, Xn независимы и распределены по Пуассону с параметрами λ1, λ2, …, λn соответственно. Тогда случайная величина X1 + X2 +… + Xn распределена по Пуассону с параметром λ1 +λ2 +… +λn.
Упражнения
1. Магазин работает десять часов в сутки. Случайные величины X1, X2, …, X10 — количество посетителей магазина в течение первого, второго и т. д. часа работы. Известно, что каждая из этих величин имеет распределение Пуассона с параметром λ1, λ2, …, λ10 соответственно. Укажите распределение числа посетителей магазина за сутки. Чему равно среднее число посетителей магазина за сутки?

154 Глава 3. Некоторые важные распределения вероятностей
Таблицы. Для распределений Пуассона составлены как таблицы вероятностей (2.1.1), так и таблицы накопленных вероятностей, т. е. функций распределения
x |
m |
|
|
|
|
P( X ¶ x) = mX=0 e−λ λm! . |
(2.1.10) |
|
Для целых неотрицательных x и различных значений λ>0 такие таблицы можно найти, например, в [4, 18, 21], а также в других сборниках статистических таблиц.
В книге [4], например, даны подробные таблицы для p(m, λ). Значения λ изменяются с шагом 0,1 в пределах от 0,1 до 15,0; значения m изменяются с единичным шагом в тех пределах, где p(m, λ) >5 ·10−7 . Более подробные таблицы для p(m, λ) даны в книге [18], где λ изменяется до 205.
Как и для биномиальных распределений, таблицы для пуассоновских вероятностей сейчас не столь необходимы, как это было в прошлом. Теперь для хорошего карманного калькулятора прямое вычисление вероятности p(m, λ) не представляет большого труда.
Таблицы функций распределения (2.1.10) весьма полезны и сейчас. Например, в [21] приведены таблицы накопленных вероятностей (2.1.10) для λ = 0,01(0,01) 1(0,05) 5(0,10) 10(0,50) 20(1,00) 30(5,00)50, точность которых не ниже чем 0,5 ·10−4 .
Для математической статистики часто необходимы вероятности вида P( X ¾x). Эти вероятности можно получить с помощью таблиц для функции (2.1.10), поскольку для целых x ¾0 справедливо равенство
P( X ¾ x) = 1 −P( X ¶ x −1).
Связь с другими распределениями. 1. Выше, в § 1 настоящей главы, уже была указана связь между распределением Пуассона и биномиальным распределением: при больших n и малых p действует приближенное равенство
Cm pm(1 −p)n−m ≈ λm e−λ для m = 0, 1, …,
n m!
где λ=np. Это соотношение есть следствие следующего предельного утверждения.
Теорема 2.1.2. Для всякого m =0, 1, … выполняется равенство
lim |
m |
p |
m |
(1 −p) |
n−m = |
e |
−λ λm |
(2.1.11) |
n→∞, p→0 |
Cn |
|
|
m! , |
если существует lim np =λ>0.
n→∞, p→0
§ 2. Распределение Пуассона |
155 |
||
|
|
|
|
Доказательство. Заметим, что |
|
|
|
Cm |
= n(n −1)…(n −m +1) |
, |
|
n |
m! |
|
|
а (1 −p)n−m можно записать в виде
(1 −p)n−m = (1 −p)n(1 −p)−m = eln(1−p)n (1 −p)−m = enln(1−p) (1 −p)−m.
С учетом сделанных замечаний перепишем Cnm pm(1 −p)n−m в виде
Cnm pm(1−p)n−m = [(np)(np−p)…(np−(m−1) p))]enln(1−p)(1−p)−m m1! .
Для вычисления предела этого выражения при n →∞, p →0 воспользуемся тем, что предел произведения равен произведению пределов (когда те существуют).
Очевидно, что первые m сомножителей в пределе дают λm и что
предел функции |
(1 |
− p) |
−m |
равен 1. Для вычисления |
|
lim |
0 e |
nln(1−p) |
||
|
n |
→ |
∞, p |
→ |
|
|||||
|
|
|
|
|
|
|
|
|
||
заметим, что n ln(1 −p) →−λ и что ex — непрерывная функция переменной x. Поэтому
(1 −p)n = enln(1−p) → e−λ.
Собранные вместе, эти результаты доказывают соотношение (2.1.11). 2. Распределение Пуассона с параметром λ>9 может быть прибли-
жено нормальным распределением со средним λ и дисперсией λ. Эта аппроксимация основана на следующей предельной теореме.
Теорема 2.1.3. Пусть случайная величина X распределена по Пуас-
сону с параметром λ. Тогда при λ→∞ распределение случайной вели- p
чины ( X −λ)/ λ сходится к стандартному нормальному распределению N(0, 1).
Эта теорема означает, что равномерно по z R1 при λ→∞ выпол-
няется соотношение
P Xp−λ ¶ z → Φ(z), (2.1.12)
λ
где Φ(z) — функция стандартного нормального распределения (о нормальном распределении см. п. 4 этой главы).
С учётом свойств нормального распределения отсюда следует, что равномерно по x1 <x2 при λ→∞ выполняется соотношение
|
h |
|
x2 −λ |
|
|
x1 −λ |
i |
|
|
P( x1 |
¶ X ¶ x2) − Φ |
|
pλ |
−Φ |
|
pλ |
|
→ 0. |
(2.1.13) |
|
|
|
|
|
|
|
|
|
|
Данная теорема может быть доказана непосредственно (доказательства мы не приводим), а может быть получена как следствие центральной предельной теоремы. (О центральной предельной теореме см. гл. 4.)

156 Глава 3. Некоторые важные распределения вероятностей
Как это принято, приведенную теорему о пределе вероятностей истолковывают как способ приближенного вычисления вероятно-
стей: считают, что если «λ достаточно велико», то |
|
P( x1 ¶ X ¶ x2) ≈ Φ x2p−λλ −Φ x1p−λλ . |
(2.1.14) |
Вопрос о том, сколь велико должно быть λ, чтобы соотношение (2.1.14) можно было использовать для приближенных вычислений, зависит от того, какую точность в приближенном равенстве (2.1.14) мы готовы признать удовлетворительной. Практика статистических применений с принятыми там требованиями точности и вычислительные эксперименты привели к указанной выше рекомендации о применении нормальной аппроксимации.
Упражнения
1.Обозначим через X число посетителей магазина в течение недели. Из наблюдений известно, что X имеет распределение Пуассона
спараметром λ=7000. Используя нормальное приближение, вычислите вероятность событий: а) P( X ¶6800); б) P(6850 ¶X ¶7150).
2.Число опасных гидрометеорологических явлений (ураганов, градов, паводков, лавин и т. п.) в течение года на территории России распределено по Пуассону со средним значением 350 (это примерный округленный показатель). Используя нормальное приближение, вычислите вероятность того, что число подобных явлений в течение года превысит: а) 380 1; б) 400.
2.2.Компьютерный практикум
Вэтом пункте обсуждаются расчеты на компьютере в пакете EXCEL вероятностей пуассоновского распределения двух типов: вероятности конкретного исхода P( X =k) и накопленной вероятности P( X ¶ k), а также и методы моделирования случайной величины, распределенной по закону Пуассона.
2.2.1. Вычисление вероятностей. Вычисление вероятностей событий вида P( X = k) для случайной величины X, имеющей распределение Пуассона, мы уже обсуждали в п. 2.6 гл. 1. Для этих целей в EXCEL используется функция ПУАССОН. Эта же функция используется и для вычисления вероятностей вида P( X ¶k). Напомним, что функция ПУАССОН входит в группу функций Статистические и имеет три аргумента: X — в этом поле вводится значение k, которое может
1 По данным Росгидромета число опасных гидрометеорологических явлений в 2006 г. составило 387. Это рекордное значение за последние пятнадцать лет.
§ 2. Распределение Пуассона |
157 |
|
|
принимать пуассоновская случайная величина (число происшедших событий), Среднее — в этом поле вводится параметр распределения Пуассона λ. Третьим аргументом функции, который нужно ввести в поле Интегральная, является значение 0 (ЛОЖЬ) или 1 (ИСТИНА). Этот аргумент задает вид вычисляемой вероятности: при 0 это вероятности вида P( X =k), при 1 — вероятности вида P( X ¶k).
Пример 3.2.1. Предположим, что мимо дома в дневные часы проезжает в среднем 15 автомобилей в минуту. Пусть случайная величина X — число автомобилей, проехавших мимо дома в минуту, и эта величина имеет закон распределения Пуассона. Чему равны следующие вероятности:
1)P( X =k), k =0, 1, 2, …, 30?
2)P(10 ¶X ¶20)?
Вычислим вероятности P( X =k) для заданного массива из 31 элемента: k = 0, 1, …, 30. Для этого сначала подготовим массив с заданными значениями, поместив эти значения, например, в ячейки A1—A31. Затем, поместив курсор в ячейку B1, вызовем процедуру вставки функции, нажав левую клавишу мыши на поле fx . В открывшемся окне мастера функций выберем в поле Категория: значение
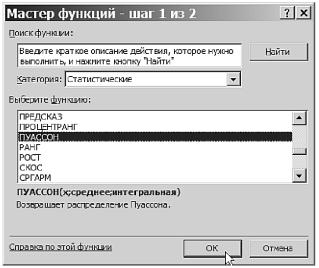
Статистические, в а поле Выберите функцию: — ПУАССОН. Заполнение полей указано на рис. 3.15.
Рис. 3.15. Заполнение полей для вызова функции ПУАССОН
158 Глава 3. Некоторые важные распределения вероятностей
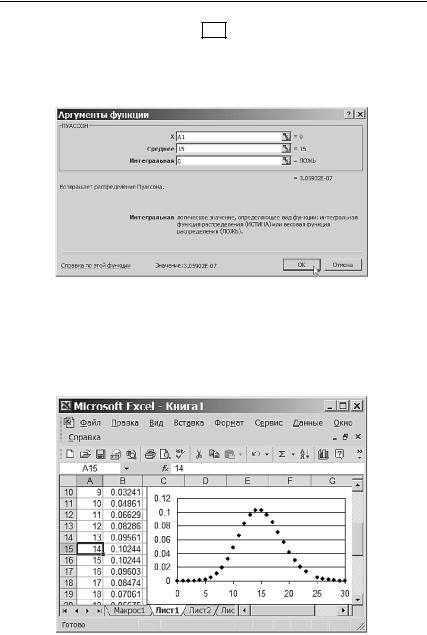
Подтвердив выбор кнопкой OK , перейдем к вводу аргументов этой функции, как показано на рис. 3.16. В поле Среднее нужно ввести параметр λ, который в нашем примере равен 15. В поле Интегральная введем 0 (ЛОЖЬ), что соответствует вычислению вероятности конкретного исхода.
Рис. 3.16. Заполнение полей для ввода аргументов функции ПУАССОН
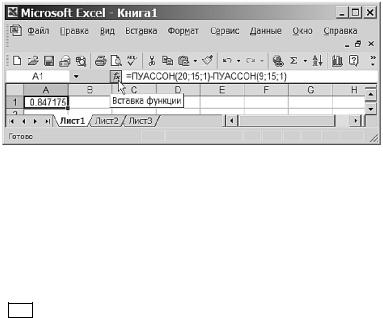
Затем скопируем соответствующую функцию в ячейки столбца B (для результатов вычислений), протянув маркер заполнения до нужной ячейки. Результаты вычислений и график, построенный средствами EXCEL, изображены на рис. 3.17.
Рис. 3.17. Результаты вычисления вероятностей P( X = k), k = 0, 1, …, 30, с помощью функции ПУАССОН и график соответствующих вероятностей
§ 2. Распределение Пуассона |
159 |
|
|
Как видно из рис. 3.17, в этом примере наибольшая вероятность, приблизительно равная 0,1, достигается при двух значениях: k =14 и k = 15. Чтобы вычислить P(10 ¶ X ¶20), можно воспользоваться функцией ПУАССОН, если выразить искомую вероятность P(10 ¶ X ¶ ¶20) =P( X ¶20) −P( X ¶9) =F(20) −F(9) через функцию распределения F в двух точках (20 и 9). Для вычисления функции распределения в качестве третьего аргумента функции ПУАССОН следует выбрать 1 (ИСТИНА). Таким образом, отметив курсором ячейку для помещения результата вычислений (например, A1) и введя в поле вставки функции fx выражение = ПУАССОН(20; 15; 1) −ПУАССОН(9; 15; 1), получим искомую вероятность, равную 0,847 после округления. Результат вычислений приведен на рис. 3.18.
Рис. 3.18. Результат вычисления вероятности P(10 ¶ X ¶ 20) с помощью функции
ПУАССОН
2.2.2. Моделирование пуассоновского распределения. Вызовем знакомую нам процедуру Генерация случайных чисел из меню Анализ данных и выберем в открывшемся окне в поле Распределение: Пуассона. В поле Лямбда= введем значение параметра этого распределения
λ. Заполним также поля Число_переменных:, Число_случайных_чисел: и Выходной_интервал:. После утверждения заданных значений клавишей OK получим в электронной таблице сгенерированную последовательность пуассоновских величин.
Пример 3.2.2. Смоделируем 50 значений пуассоновской случайной величины с параметром λ=0,365. Например, этими значениями могут быть количества страховых случаев в год, заключенных по 50 страховым договорам, если среднее число страховых случаев в год равно параметру λ = 0,365. (Обратите внимание на то, что в этом примере параметр λ не является целым числом. Обсуждение этого примера и объяснение, почему мы взяли λ=0,365, приведено ниже
160 Глава 3. Некоторые важные распределения вероятностей
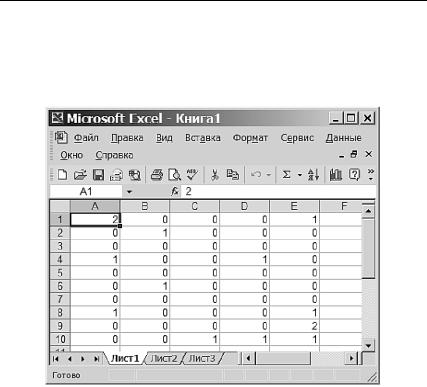
в § 3 гл. 4, где показано, как вычисление биномиальных вероятностей можно заменить вычислением пуассоновских вероятностей.) На рис. 3.19 изображена сгенерированная последовательность из 50 чисел, распределенных по закону Пуассона с параметром λ=0,365.
Рис. 3.19. Сгенерированная последовательность из 50 чисел, распределенных по закону Пуассона с параметром λ=0,365
Обратите внимание на то, что в этом случайном эксперименте ни по одному из 50 страховых договоров не наступило более двух страховых случаев, по 10 договорам наступил один страховой случай и лишь по двум договорам — два страховых случая.
2.3. Задачи
1. Пусть X1 и X2 — две независимые одинаково распределенные по Пуассону случайные величины. Найдите условное распределение величины X1 при фиксированном значении X1 + X2 , т. е. вычислите P( X1 =k |X1 + X2 =n). (Здесь k, n — неотрицательные целые числа.)
2. Насекомое откладывает случайное число яиц. Предположим, что число яиц распределено по Пуассону с параметром λ. Каждое яйцо дает развитие новому насекомому, и пусть p — вероятность того, что оно достигнет взрослого состояния. Предполагая взаимную
