
tjurin_teorija_verojatn_978-5-94057-540-5_1
.pdf§ 1. Биномиальное распределение |
131 |
|
|
личина X — число девушек среди выбранных студентов. Укажите распределение случайной величины X. Вычислите вероятность событий: а) P( X =4); б) P( X <2); в) P( X ¶3).
4. Вероятность того, что пассажир, купивший авиабилет, по различным причинам не полетит рейсом, указанным в билете, равна 0,01. В самолете 200 мест. Считая, что все пассажиры ведут себя независимо друг от друга, укажите распределение случайной величины X — числа пассажиров, летящих своим рейсом.
Математическое ожидание и дисперсия. Покажем, что для случайной величины X, имеющей биномиальное распределение, справедливы равенства
EX = np, DX = npq. |
(1.1.2) |
По определению математического ожидания
n |
|
EX = Xk=0 kP( X = k | n, p); |
(1.1.3) |
по определению дисперсии DX =EX2 −(EX)2, причем
Xn
EX2 = k2 P( X = k | n, p).
k=0
Но вычисления по этим формулам довольно сложны, и проще (и правильнее) поступать иначе. Введем для каждого отдельного испытания Бернулли случайную величину Y , которая может принимать только два значения: Y =1, если испытание закончилось «успехом», и Y =0, если «неудачей». Пронумеруем отдельные испытания Бернулли числами 1, 2, …, n и те же номера дадим соответствующим им случайным величинам Y : Y1 , Y2 , …, Yn. Теперь X — число успехов в n испытаниях — можно представить как X =Y1 +Y2 +… +Yn. Случайные слагаемые в этой формуле независимы (потому что независимы испытания Бернулли) и одинаково распределены. Поэтому по свойствам математических ожиданий и дисперсий
EX = E(Y1 +Y2 +… +Yn) = EY1 +EY2 +… +EYn = nEY1, DX = D(Y1 +Y2 +… +Yn) = DY1 +DY2 +… +DYn = nDY1.
Далее, EY1 =1 ·p +0 ·q = p,
DY1 = EY12 −(EY1)2 = p −p2 = pq.
Из этого следуют формулы (1.1.2) и (1.1.3).

132 Глава 3. Некоторые важные распределения вероятностей
Упражнения
1.Игральную кость бросают 6 раз. Пусть случайная величина X равна числу выпавших шестерок в этом эксперименте. Найдите математическое ожидание и дисперсию величины X.
2.В студенческой группе 15 девушек и 5 юношей. Из этой группы случайным образом выбирают 4 студентов. Пусть случайная величина X — число девушек среди выбранных студентов. Укажите математическое ожидание и дисперсию случайной величины X.
3.Тест проверки знаний содержит 30 вопросов на разные темы. На каждый вопрос даны четыре варианта ответов, лишь один из которых правильный. Найдите среднее число правильных ответов, если отвечающий выбирает ответ случайно, не читая его содержание. Найдите дисперсию числа правильных ответов, выбираемых указанным выше способом.
4.Вероятность встретить заданный признак у обследуемого респондента равна p = 0,4. Найдите математическое ожидание и дисперсию числа респондентов, обладающих этим признаком, при опросе 20 человек.
5.Нарисуйте график зависимости дисперсии биномиальной случайной величины как функции от параметра p. При каком значении p дисперсия биномиальной случайной величины будет наибольшей при фиксированном значении n? (Это упражнение имеет важное значение при расчете объема социологической выборки. Мы обсудим эту тему в § 3 гл. 4.)
6.Случайные величины X и Y имеют биномиальные распределения: X — с параметрами n =10 и p =0,2, а Y — с параметрами n =10
иp =0,4. Дисперсия какой из этих случайных величин больше?
7.Случайные величины X и Y имеют биномиальные распределения: X — с параметрами n =10 и p =0,3, а Y — с параметрами n =10
иp =0,6. Дисперсия какой из этих случайных величин больше?
Таблицы. Для биномиального распределения, как и для других распределений вероятностей, есть два типа таблиц.
В таблицах первого типа приводятся вероятности P( X = k) при различных значениях p и n. Например, в книге [4] приведены таблицы значений P( X =k |n, p) (с пятью десятичными знаками) для n от 5 до 30 с шагом по n, равным 5 (краткое обозначение: n =5(5)30), и p =0,01; 0,02 (0,02); 0,10 (0,10); 0,50. Последнее выражение для p означает, что в таблицах есть значения для p =0,01, для p =0,02, далее p изменяется с шагом 0,02 до 0,10, и со значения p =0,1 оно изменяется с шагом 0,1 до 0,5.

§ 1. Биномиальное распределение |
133 |
|
|
В таблицах второго типа даны значения накопленных вероятностей биномиального распределения, т. е. значения
Xk
P( X ¶ k | n, p) = P( X = m | n, p).
m=0
Например, в книге [21] вероятности P( X ¶k |n, p) даны для n=1(1)25, p = 0,005 (0,005); 0,02 (0,01); 0,10 (0,05); 0,30 (0,10); 0,50, для
k=0(1)n.
Вописаниях таблиц обычно можно найти указания, как поступать, если интересующие нас значения n и/или p в данных таблицах отсутствуют (см., например, [4]).
Замечание. Значения вероятностей P( X =k) биномиального распределения с параметром p >0,5 легко получить, зная соответствующие вероятности при p <0,5. Действительно, если вероятность «успеха» p >0,5, то вероятность «неудачи» q =1 −p <0,5. Поменяв названия «успех» и «неудача» одно на другое, мы сведем случай p > 0,5 к p <0,5. Другими словами,
P( X = k | n, p) = P( X = n −k | n, 1 −p).
Это свойство учитывается при составлении статистических таблиц биномиального распределения.
Приближенные вычисления. Табличные значения для вероятностей P( X =k |n, p) и P( X ¶k |n, p), как было указано выше, обычно приводятся для значений n, не превышающих 25—30. Однако во многих практических задачах значение n может быть существенно большим. В этом случае прибегают к приближенным вычислениям. Однако сам способ этих вычислений зависит не только от значения n, но и от величины p. Ниже будут рассмотрены два возможных способа приближенных вычислений и указаны ситуации, в которых их следует применять.
1. Нормальное приближение (нормальная аппроксимация). Биномиальное распределение с параметрами n и p может быть приближено нормальным распределением со средним np и дисперсией npq=np(1 −p), если выполняются условия np(1 −p) ¾5 и 0,1 ¶p¶0,9. При условии np(1 −p) ¾25 эту аппроксимацию можно применять вне зависимости от значения p.
Указанная аппроксимация основана на математическом факте, называемом теоремой Муавра—Лапласа (см. п. 3.1 гл. 4).
Пусть X — число успехов в n испытаниях Бернулли и p — вероятность успеха. Тогда при n →∞ и фиксированном p распределение случайной величины ( X −np)/pnpq сходится к стандартному нормальному распределению N(0, 1).

134 Глава 3. Некоторые важные распределения вероятностей
Это означает, что в указанных условиях равномерно по z полняется соотношение
|
X −np |
|
Φ |
|
||
|
|
|
|
|
||
P pnpq ¶ z → |
|
(z), |
||||
R1 вы- (1.1.4)
где Φ(z) — функция распределения вероятностей стандартного нормального закона. О нормальных распределениях смотрите § 4 этой главы.
Из соотношения (1.1.4) и свойств нормального распределения следует,
|
h |
|
x2 |
−np |
|
x1 −np |
i |
|
|
|
P( x1 ¶ X ¶ x2) − |
Φ |
|
pnpq |
− |
Φ |
pnpq |
|
→ 0 |
(1.1.5) |
|
|
|
|
|
|
|
|
|
|
|
|
что равномерно по x1 <x2 при n →∞. Как это принято, теорему Муав- ра—Лапласа (1.1.4) о пределе вероятностей истолковывают как способ приближенного вычисления этих вероятностей: считают, что «если n достаточно велико», то
|
X −np |
¶ |
z ≈ |
Φ |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а |
P pnpq |
|
|
|
(z), |
|
x1 −np |
|
|
|||||||||
|
|
|
Φ |
|
x2 −np |
|
|
Φ |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
P( x1 ¶ X ¶ x2) ≈ |
|
|
pnpq |
|
− |
|
pnpq |
. |
(1.1.6) |
||||||||
Последняя формула означает, что при больших n вместо биномиального распределения можно использовать нормальное распределение N(np, npq). Более точное приближение дают формулы «с поправкой на непрерывность»: для целых x1 <x2 имеем
|
Φ |
x2 |
−np +0,5 |
|
|
Φ |
|
x1 |
np −0,5 |
|
|
||||
P( x1 ¶ X ¶ x2) ≈ |
|
|
|
|
|
|
− |
|
|
|
− |
. |
(1.1.7) |
||
|
p |
|
|
|
|
p |
|
|
|||||||
|
npq |
|
|
npq |
|||||||||||
Вопрос о том, как велико должно быть n, чтобы эти соотношения можно было использовать для приближенного вычисления, совсем не прост. Ответ на него зависит не только от n, но и от p, и от того, какую точность в приближенном равенстве (1.1.6) мы готовы признать удовлетворительной. (Иными словами, меньше чего должно быть различие между левой и правой частями в формуле (1.1.6), чтобы на это различие не обращать внимание.) Практика статистических применений с принятыми там требованиями точности и вычислительные эксперименты привели к указанным выше рекомендациям о пределах применимости нормальной аппроксимации.
2. Пуассоновское приближение. Биномиальное распределение с параметрами n и p может быть приближено распределением Пуассона с параметрами np, если p <0,1 и n достаточно велико.
Эта аппроксимация основана на следующей теореме. Пусть X — число успехов в n испытаниях Бернулли, p — вероятность успеха.
§ 1. Биномиальное распределение |
135 |
|
|
Предположим, что n →∞, p →0, причем λ = np при этом остается постоянным. Тогда
P( X = m) → e−λ λm для m = 0, 1, … m!
(О распределении Пуассона и доказательстве этой теоремы см. § 2 настоящей главы.)
Как принято в математике, эти результаты о пределах вероятности используют для приближенного вычисления этих вероятностей: считают, что «если n достаточно велико, а p достаточно мало», то
m |
|
|
P( X = m) ≈ e−λ λm! , |
m = 0, 1, …, |
(1.1.8) |
x |
m |
|
P( X ¶ m) ≈ e−λ mX=0 |
|
|
λm! , x = 0, 1, … |
(1.1.9) |
Как и в случае нормальной аппроксимации, ответ на вопрос о границах для n, p и pn, при которых можно пользоваться приближенными равенствами (1.1.8) или (1.1.9), зависит от требований точности. Приведенная выше рекомендация простая, но довольно грубая.
По вопросу о точности нормального или пуассоновского приближений приведем мнение авторов книги [4]. (В цитате изменены номера упоминаемых формул.) «Основной недостаток приближенных формул (1.1.7) и (1.1.9) — малая точность при тех значениях n, которые характерны для большинства практических приложений. Недостатком нужно считать отсутствие четких рекомендаций, в каких случаях следует применять формулу (1.1.7), а в каких — (1.1.9). В силу указанных причин, например, при n <200 обе эти формулы пригодны лишь для грубых, ориентировочных расчетов». Это было написано в 1965 г. В настоящее время приближенные формулы для вычисления биномиальных вероятностей нужны только для действительно больших n. Для «умеренных» n точные значения можно получить с помощью компьютера.
Упражнения
1.Правильную монету подбрасывают n =100 раз. Вычислите приближенно вероятность того, что число выпавших гербов меньше:
а) 30 (является ли это событие практически невозможным?); б) 40; в) 45. Какую из описанных аппроксимаций для этого надо
использовать?
2.Случайная величина X имеет биномиальное распределение вероятностей с параметрами n =36 и p =1/2. С помощью нормальной аппроксимации вычислите вероятность события ( X > 24). Является

136 Глава 3. Некоторые важные распределения вероятностей
ли это событие практически невозможным? (Свяжите эту задачу
сописанным выше примером исследования воздействия препарата на скорость реакции человека. Какое решение следует, на ваш взгляд, принять, если число успехов в этом эксперименте превысит 24?)
3.Вероятность того, что пассажир, купивший авиабилет, по различным причинам не полетит рейсом, указанным в билете, равна 0,01. В самолете 200 мест. Авиакомпания продала на рейс 202 билета. Вычислите вероятность того, что у компании не возникнет проблем
сотправкой пассажиров на этом рейсе, т. е. число зарегистрировавшихся пассажиров не превысит числа мест в самолете.
4.В выборочном социологическом опросе было опрошено 1500 избирателей. При этом 6% из них заявили, что будут голосовать за некоторую партию. Используя нормальное приближение, вычислите вероятность того, что во время выборов за эту партию проголосует менее 5% процентов электората.
1.2.Компьютерный практикум
Вэтом пункте обсуждаются методы моделирования биномиально распределенной случайной величины X, расчет на компьютере в пакете EXCEL вероятностей биномиального распределения двух типов: вероятности конкретного исхода P( X = k) и накопленной P( X ¶k) при различных значениях параметров n и p.
1.2.1. Моделирование серии испытаний Бернулли с произвольной вероятностью успеха в одном испытании. Рассмотрим задачи, связанные с моделированием результатов независимых испытаний, которые можно описать схемой испытаний Бернулли. В п. 1.3 гл. 1 мы уже имели дело с такими испытаниями. Там был рассмотрен эксперимент, имитирующий бросание симметричной монеты. Было показано, что такой эксперимент легко осуществить на компьютере, сгенерировав последовательность из единиц (успех) и нулей (неудача) заданной длины (число экспериментов). Вы уже знаете, что
вEXCEL для моделирования такого эксперимента нужно вызвать команду Анализ данных, которая вызывается из главного меню панели управления Сервис. В появившемся после вызова этой команды окне
всписке Инструменты анализа следует выбрать процедуру Генерация случайных чисел, как было показано на рис. 1.5 и рис. 1.6. Применим эту же процедуру для генерирования случайных последовательностей
виспытаниях Бернулли с другим параметром p (в эксперименте с бросанием монеты p =0,5).
Пример 3.1.1. Смоделируем результаты тройного теста, о котором идет речь в упражнении 3 п. 3.2 гл. 1. В этом упражнении дегустатору
§ 1. Биномиальное распределение |
137 |
|
|
чая несколько раз предъявляются три чашки чая, две из которых с чаем одного сорта, а третья — с чаем другого сорта. Дегустатор должен определить чашку, в которой чай отличается. Результаты этих испытаний можно записать в виде последовательности единиц (правильное определение) и нулей (ошибочное определение); причем если в результате одного эксперимента дегустатор выбирает чашку чая наугад, то вероятность успеха (правильного ответа) равна p =1/3. Если дегустатор может различать сорта чая, то вероятность правильного ответа в одном испытании должна быть больше 1/3. Предполагая, что за время испытаний, которые проходят в одних и тех же условиях, способность дегустатора различать сорта чая не меняется, мы приходим к схеме испытаний Бернулли с вероятностью успеха в одном испытании p. Смоделируем результаты этих испытаний в двух случаях:
1)дегустатор выбирает ответ случайным образом с вероятностью p =1/3;
2)дегустатор способен с большой вероятностью, например, с вероятностью p =0,9 определить чашку с отличающимся сортом чая.
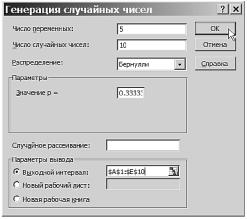
Предположим, что было проведено 5 экспериментов в серии из 10 испытаний в каждом эксперименте для двух разных p. Вызвав процедуру Генерация случайных чисел, заполним все поля, как и в примере п. 1.3 гл. 1 (см. рис. 1.7), изменив только значение вероятности, поставив в поле Значение p = число 0,33333 (в этом поле нужно обязательно ввести число, а не выражение). Результаты моделирования
Рис. 3.2. Окно задания параметров процедуры для моделирования пяти экспериментов по 10 серий в каждом при p =0,33333

138 Глава 3. Некоторые важные распределения вероятностей
Рис. 3.3. Результаты генерирования случайных последовательностей Бернулли
будут помещены в 5 первых столбцов A −E начиная с ячейки A1. Заполнение окна для моделирования пяти экспериментов по 10 серий испытаний в каждом с p =0,33333 показано на рис. 3.2.
Затем вызовем ту же процедуру с другим значением p =0,9. Результаты этого моделирования будут записаны в ячейки столбцов G −K начиная с ячейки G1, так что эксперименты с различными p разделены пустым столбцом. Результаты генерирования десяти последовательностей длины 10 каждая для двух различных p изображены на рис. 3.3.
Обсудим результаты моделирования тройного теста. Обратите внимание на то, что в первом блоке экспериментов (при p = 1/3), хотя общее число правильных ответов во всех пяти экспериментах невелико (12), в отдельных экспериментах результаты подвержены сильной изменчивости — в них число правильных ответов изменялось от 1 до 5. У дегустатора-эксперта (с p =0,9) число правильных ответов в одном эксперименте большое — от восьми до десяти.
1.2.2. Моделирование биномиально распределенной случайной величины. Покажем, как в пакете EXCEL смоделировать случайные величины, распределенные по биномиальному закону. Для моделирования биномиально распределенной случайной величины можно было бы использовать уже известный нам метод генерирования последовательности испытаний Бернулли (он рассмотрен выше на примере теста дегустатора). Получив серию успехов и неудач при

§ 1. Биномиальное распределение |
139 |
|
|
заданном числе испытаний n, нужно вычислить число успехов в этой последовательности (например, сложить результаты всех испытаний, если мы кодируем единицей успех, а нулем — неудача). Такая случайная величина — число успехов в n испытаниях Бернулли с вероятностью успеха в одном испытании p — распределена по биномиальному закону с параметрами n и p. Однако в EXCEL можно генерировать случайные величины, распределенные по биномиальному закону, непосредственно. Напомним, что генерация случайных чисел производится вызовом одноименной процедуры из меню Анализ данных (оно вызывается из главного меню Сервис). Вызвав окно Генерация случайных чисел, заполним в нем соответствующие поля.
Пример 3.1.2. Смоделируем, например, 5 серий биномиально распределенных случайных величин с одними и теми же параметрами n =100, p =0,2. Для этого в поле Число переменных: введем 5, в поле Число случайных чисел: поставим 1, в поле Распределение: выберем из предлагаемых распределений Биномиальное. В следующей части окна введем два параметра биномиального распределения, заполнив соответствующие два поля. В поле Значение p = введем 0,2, а в поле Число испытаний = введем 100. Результаты вычислений поместим в ячейки первых пяти столбцов, задав в поле Выходной интервал: адрес ячеек электронной таблицы для записи результатов вычисления. Результат заполнения полей процедуры показан на рис. 3.4.
Рис. 3.4. Заполнение полей для вызова процедуры генерации пяти биномиально распределенных случайных величин
140 Глава 3. Некоторые важные распределения вероятностей
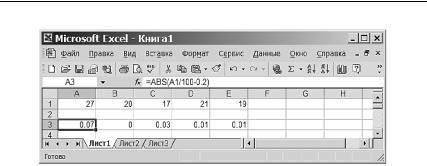
Рис. 3.5. Результаты генерации пяти биномиально распределенных случайных величин
На рис. 3.5 в первой строке электронной таблицы приведены результаты этого моделирования.
Проанализируем полученные результаты. Из первой строки таблицы (см. рис. 3.5) видно, что все числа разные. В третьей строке таблицы мы дополнительно записали абсолютные величины отклонений
частот успехов от истинного значения вероятности успеха в одном |
|||
испытании, т. е. величины |
X |
−p , вызвав соответствующую матема- |
|
n |
|||
|
|
|
|
тическую функцию ABS. Это |
отклонения |
наблюдаемых частот собы- |
|
тия (числа успехов, поделенного на число испытаний) от теоретического значения p вероятности успеха. Только в одном случае из пяти
эти отклонения превосходят заданную ошибку ǫ=0,05. Ниже мы вы- |
|||||
числим вероятность события P |
|
X |
−p |
¾0,05 |
. Она окажется равной |
n |
|||||
|
|
|
|
|
|
примерно 0,26. |
|
|
|
|
|
1.2.3. Вычисление биномиальных вероятностей вида P( X =k). Как уже было сказано в § 1 этой главы, биномиальное распределение — это распределение числа успехов в n испытаниях Бернулли с вероятностью успеха в одном испытании p. Оно зависит от этих двух параметров — n и p. Случайная величина, распределенная биномиально, может принимать n +1 значение: 0, 1, …, n.
Пример 1. Пусть p =0,5 и n =10. Число успехов при этих параметрах может принимать только целые значения от 0 до 10 включительно. Поэтому подготовим сначала в электронной таблице столбец с этими значениями: 0, 1, 2, …, 10. Затем с помощью статистической функции БИНОМРАСП создадим новый столбец из вероятностей, соответствующих этим значениям. Эта функция входит в группу статистических функций. Вызов функций из этой группы мы уже рассматривали в гл. 1, п. 2.6. Напомним, как это можно сделать. Поместим
