
tjurin_teorija_verojatn_978-5-94057-540-5_1
.pdf
|
|
|
§ 4. Нормальное распределение |
|
|
181 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
0,5 |
0,68 |
1 |
1,2 |
1,5 |
1,65 |
2 |
2,3 |
2,6 |
3 |
|
|
||||||||||
Φ( x) |
0,5000 0,6915 0,7517 0,8413 0,8849 0,9332 0,9505 0,9773 0,9893 0,9953 0,9987 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
выполните следующие упражнения. (Далее под Z понимается стандартная нормальная случайная величина.)
1.Найдите P(Z ¶0,5) и P(Z ¾0,5).
2.Найдите P(Z ¶2,6) и P(Z ¾2,6).
3.Найдите P(Z ¶−0,5) и P(Z ¾−0,5).
4.Найдите P(−2,3 ¶Z ¶2,3).
5.Найдите P(0,5 ¶Z ¶1,2).
6.Найдите P(−0,5 ¶Z ¶1,65).
7.Найдите P(−2,3 ¶Z ¶−0,5).
8.Найдите P(|Z −1|¾0,5).
9.Для p = 0,75 найдите приблизительное значение квантили xp стандартного нормального распределения.
10.Для p =0,25 найдите приблизительное значение квантили xp стандартного нормального распределения.
11.Для p =0,95 найдите приблизительное значение квантили xp стандартного нормального распределения.
12.Для p =0,975 найдите приблизительное значение квантили xp стандартного нормального распределения.
Математическое ожидание, дисперсия и другие числовые характеристики. Заметим, что достаточно знать, каковы моменты (математическое ожидание, дисперсия и т. д.) стандартной нормальной случайной величины Z N(0, 1), чтобы сказать, каковы моменты величины N(a, σ2 ). Действительно, если X N(a, σ2 ), то согласно соотношению (4.1.5) можно считать X линейной функцией случайной величины Z N(0, 1):
X = a +σZ.
Поэтому по свойствам математических ожиданий и дисперсий
EX = a +σEZ, DX = σ2 DZ.
Математическое ожидание EZ вычисляется легко
+∞ |
+∞ |
|
|
|
|
|
EZ = Z |
xϕ( x) dx = Z |
x |
x2 |
|
||
p |
|
πe− |
2 dx = 0, |
|||
2 |
||||||
−∞ −∞

182 Глава 3. Некоторые важные распределения вероятностей
так как подынтегральная функция xϕ( x) нечетная (как можно увидеть (−x)ϕ(−x) =−xϕ( x)). Как известно, интеграл от любой нечетной функции по симметричной области равен 0.
Следовательно,
EX = a, если X N(a, σ2 ).
Дисперсия Z N(0, 1) вычисляется несколько сложнее. Заметим прежде всего, что
DZ = EZ2 −(EZ)2 = EZ2,
поскольку EZ =0. Затем интеграл, выражающий EZ2:
+∞
EZ2 = Z |
2 |
2 |
|
|
px2 |
πe− |
x |
dx, |
|
2 |
||||
−∞
«интегрированием по частям» сводится к уже известному нам интегралу (4.1.3). Так получаем, что DZ = 1. Поэтому DX = σ2 , если
X N(a, σ2 ).
Из других числовых характеристик нормального распределения упомянем медиану, или 50%-ную квантиль. Так как плотность f ( x) распределения N(a, σ2 ) симметрична относительно точки x =a, точка a является медианой этого распределения.
Упражнения
1. Найдите E(Z3) и E|Z|.
2. Пусть X N(1, 4). Найдите E(2 X + 1) и D(2 X +1). Вычислите
P(0 < X <5) и P(−3 < X <5).
3. Пусть X N(a, σ2 ). Используя таблицу 4.1, выразите межквартильный размах x0,75 −x0,25 этой случайной величины через ее стандартное отклонение σ.
Распределение суммы. На практике часто приходится сталкиваться с суммами независимых случайных величин. В общем случае расчет распределения суммы случайных величин может быть довольно непростой задачей. Распределение суммы случайных величин, как правило, отличается от распределений суммируемых величин, причем не только по значениям параметров, но и по своему характеру. Однако для нормального распределения вероятностей справедлива следующая полезная теорема.
Теорема. Сумма двух независимых нормальных величин тоже рас-
пределена нормально.

§ 4. Нормальное распределение |
183 |
|
|
Доказательство. Пусть X1 N(a1 , σ12 ), X2 N(a2 , σ22 ) и случайные величины X1 и X2 независимы. Мы сделаем даже больше, чем утверждает теорема: мы покажем, мы не только покажем, что X1 + X2 подчиняется нормальному распределению, но и найдем параметры этого распределения. Мы докажем, что
X1 + X2 N(a1 +a2, σ12 +σ22 ).
Представим эти случайные величины X1 и X2 в виде линейных функций стандартных случайных величин Z1, Z2 N(0, 1):
X1 = a1 +σ1 Z1 , X2 = a2 +σ2 Z2 ,
причем случайные величины Z1 и Z2 независимы. Теперь
X1 + X2 = (a1 +a2) +σ1 Z1 +σ2 Z2.
Для доказательства теоремы достаточно показать, что случайная величина σ1 Z1 +σ2 Z2 распределена нормально. Для этого вычислим ее функцию распределения
F(t) = P(σ1 Z1 +σ2 Z2 ¶ t), t R1.
Совместная плотность вероятностей пары случайных величин Z1 , Z2 в точке плоскости ( x1, x2) равна
|
1 |
exp − |
x2 |
+x2 |
. |
ϕ( x1, x2) = |
1 |
2 |
|||
2π |
|
2 |
По определению величина F(t) равна интегралу от функции плотности ϕ( x1, x2) по области D, где
D = {( x1, x2) : σ1 x1 +σ2 x2 ¶ t}.
Область D (для t >0) изображена на графике рис. 3.28 а). Обратим внимание на то, что значение плотности ϕ( x1, x2) по-
стоянно на окружностях с центром в нуле. Поэтому интегралы от ϕ( x1, x2) по области D и по области D˜ , которая получается из D поворотом, равны. Область D˜ получим таким поворотом области D,
чтобы граница области D — прямая ( x1, x2) : σ1 x1 +σ2 x2 = t — стала перпендикулярна оси абсцисс. Эта «повернутая» прямая ограничи-
вает область D˜ . Точку оси абсцисс, через которую проходит граница области D˜ , обозначим h. С геометрической точки зрения, |h|— это длина перпендикуляра, опущенного из начала координат на границу области D. Из геометрических соображений |h| легко вычислить (например, подсчитав площадь треугольника двумя способами):
|
t2 t2 |
|
t2 |
|
t |
||||
|
|
|
|
|
|
|
|
|
|
h ·rσ12 + σ22 = σ1 σ2 h = |
p |
|
. |
||||||
|
σ12 +σ22 |
||||||||
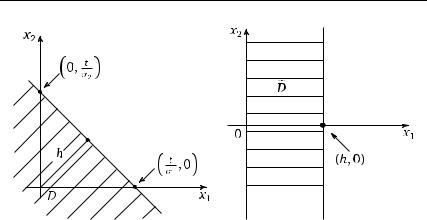
184 Глава 3. Некоторые важные распределения вероятностей
а) б)
Рис. 3.28. ) область интегрирования; ) область ˜ a б D
Следовательно
ZZ ZZ
P(σ1 Z1 +σ2 Z2 < t) = ϕ( x1, x2) dx1 dx2 = ϕ( x1, x2) dx1 dx2 =
D |
˜ |
|
D |
|
|
˜ |
|
|
t |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= P((Z1, Z2 ) |
|
D) = P(Z1 < h) = P Z1 |
< |
pσ12 +σ22 |
|
= Φ |
|
|
|
. |
|
|
• |
|
‹ •pσ12 +σ22 ‹ |
|
|||||||
Мы видим в результате, что случайная величина σ1 Z1 +σ2 Z2 подчи- |
|||||||||||
няется гауссовскому распределению с дисперсией σ2 |
+σ2 |
и нулевым |
|||||||||
математическим ожиданием: |
|
|
|
1 |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
σ1 Z1 +σ2 Z2 N(0, σ12 +σ22 ).
Отсюда немедленно следует утверждение теоремы, ибо
(a1 +σ1 Z1) +(a2 +σ2 Z2) N(a1 +a2, σ12 +σ22 ).
Упражнения
1. Случайные величины X1 и X2 имеют одно и то же нормальное распределение вероятностей: Xi N(a, σ2 ), где i =1, 2, и независимы. Найдите и сравните между собой распределения следующих случайных величин: 2 X1 и X1 + X2. У какой из этих случайных величин дисперсия меньше? (Решение этой задачи лежит в основе главного принципа формирования портфеля ценных бумаг и диверсификации биз-
§ 4. Нормальное распределение |
185 |
|
|
неса. Как работает этот принцип, будет показано в следующем упражнении.)
2.Ежедневные биржевые стоимости ценных бумаг двух компа-
ний X1 и X2 являются независимыми случайными величинами с одним и тем же нормальным законом распределения с параметрами a = 20 (рублей) и σ2 = 1. Инвестор хочет вложить капитал 40 рублей в эти по сути одинаковые ценные бумаги наиболее надежным образом. Какой из возможных портфелей ценных бумаг для него
предпочтительней: 2 X1 или X1 + X2? Для ответа на этот вопрос можно, например, посчитать вероятность 10% убытков для каждого из
портфелей, т. е. найти P(2 X1 < 36) и P( X1 + X2 <36). (Заметим, что требование одинаковой распределенности случайных величин X1
иX2 в этой задаче не существенно, а вот требования независимости
инормальности этих случайных величин весьма важны.)
3.Усложним упражнение 2. Рассмотрим независимые одинаково нормально распределенные ценные бумаги не двух, а трех компаний. Будем считать наиболее надежным портфель с наименьшей дисперсией. Какой из следующих портфелей ценных бумаг будет наиболее
надежным: 3 X1, 2 X1 + X2 или X1 + X2 + X3?
4.Пусть X1, X2, …, Xn — независимые одинаково распределенные нормальные случайные величины с параметрами a и σ2 . Найдите распределение, математическое ожидание и дисперсию среднего арифметического этих величин.
5.Пусть X1, X2 — независимые одинаково распределенные нормальные случайные величины с параметрами a и σ2 . Найдите распределение случайной величины X1 −X2.
4.2.Компьютерный практикум
Вэтом пункте обсуждаются методы вычисления на компьютере
впакете EXCEL вероятностей вида P( X ¶k), значений плотности в заданных точках и квантилей заданного уровня для произвольного нормального (гауссовского) распределения. Также проводится моделирование последовательности нормально распределенных случайных величин с заданными параметрами a и σ.
4.2.1. Вычисление вероятностей событий, связанных с нормальной случайной величиной. С этим распределением мы уже встречались, обсуждая в гл. 1 вычисление плотности распределения. Вернемся к задаче из п. 2.6 гл. 1. Мы вычислили в этом параграфе в нескольких точках значения плотности нормального распределения, по которому приближенно распределен рост девушек-студенток первого курса. Мы

186 Глава 3. Некоторые важные распределения вероятностей
приняли для роста нормальный закон с параметрами a =168, σ=6. Плотность этого закона изображена на рис. 2.5. Для ее вычисления в EXCEL мы использовали функцию НОРМРАСП. Эту же функцию можно применить для вычисления вероятностей событий вида ( X ¶b) (а значит, и событий ( X ¾a), (a ¶X ¶b)).
Пример 3.4.1. Вычислим вероятность того, что рост случайно выбранной девушки-студентки не превзойдет 175 см, т. е. P( X ¶175). Иначе говоря, нам нужно вычислить значение в точке x =175 функции нормального распределения с параметрами a = 168, σ = 6, т. е. F(175, 168, 6). Отметим в электронной таблице курсором ячейку, в которую нужно поместить результат вычислений, и вызовем функцию НОРМРАСП. Заполним в окне Аргументы функции первые три поля, как и раньше: введем соответственно 175, 168, 6. В отличие от вычисления плотности распределения, для вычисления функции распределения в четвертом поле Интегральная нужно ввести 1 (ИСТИНА), что соответствует вычислению функции распределения. Заполнение полей приведено на рис. 3.29.
Врезультате вычислений получаем значение этой вероятности
сточностью до трех значащих цифр 0,878. (А значит, вероятность того, что рост случайно выбранной студентки превзойдет 175 см, равна 0,122 — это вероятность противоположного события ( X >175)). Тот же результат можно получить по-другому, воспользовавшись вычисле-
нием функции распределения стандартного нормального закона. По- |
|
скольку F(175, 168, 6) =Φ 175 −6 |
168 , вызовем функцию НОРМСТРАСП |
и вычислим ее значение в точке Z = (175 − 168)/6. Заметим, что
Рис. 3.29. Ввод аргументов для вычисления значения функции нормального распределения в точке
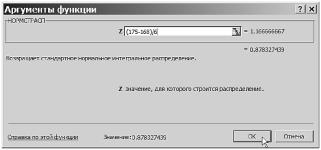
§ 4. Нормальное распределение |
187 |
|
|
Рис. 3.30. Использование функции НОРМСТРАСП для вычисления значения функции нормального распределения в точке
эта функция имеет только один аргумент и вычисляется именно функция распределения, а не плотность. В поле ввода аргумента Z можно вводить выражения (см. рис. 3.30). (Это справедливое для всех функций подобного типа свойство мы до сих пор не использовали.) Результат вычислений отображен в этом же окне внизу.
Пример 3.4.2. Решим следующую задачу. Известно, что для массового пошива одежды используют лекала разных категорий размеров. Например, для женщин принята шкала из четырех категорий размеров: 1-я категория для женщин экстра низкого роста (ЭН) соответствует росту до 156 см, 2-я категория для женщин низкого роста (Н) соответствует росту от 156 до 164 см, 3-я категория для женщин среднего роста (С) — росту от 164 см до 172 см, 4-я категория для женщин высокого роста (В) — росту от 172 см. У всех размеров одежды одной категории одинаковая длина, рассчитанная на соответствующие пропорции тела. Рассчитаем для нашей группы девушек-студенток, рост которых распределен по указанному выше нормальному закону, вероятности отнесения к каждой из четырех категорий. Тем самым мы можем приближенно предусмотреть процент одежды каждого роста в общем объеме сшитой одежды для данной группы девушек. Для единообразия вычислений примем, например, для нижней границы ЭН-роста значение 0, а для верхней границы В-роста значение 250 см. Запишем границы каждой категории роста в электронной таблице в виде двух столбцов — A и B. В столбце C запишем вероятности случайно выбранной девушки принадлежать к каждой из четырех категорий размера. Установив курсор в ячейку C1, в поле вставки функции fx введем выражение (формулу) =НОРМСТРАСП((B1−168)/6)−НОРМСТРАСП((A1−168)/6) и

188 Глава 3. Некоторые важные распределения вероятностей
Рис. 3.31. Вычисление вероятностей отнесения к четырем категориям размеров
распространим ее с помощью маркера заполнения на все 4 ячейки столбца C. Результат вычислений изображен на рис. 3.31.
Формула, записанная в строке формул, есть не что иное, как
168 |
|
168 |
— вероятность нормально распределенной |
Φ b −6 |
− Φ a −6 |
случайной величины с заданными параметрами попасть в интервал (a, b), левый и правый концы которого записаны в ячейках A1 и B1 соответственно. Обратите внимание на то, что девушки среднего роста (с третьей категорией размера) составляют около 50%.
4.2.2. Вычисление плотности нормального распределения. Гауссовская случайная величина принимает значения на всей действительной прямой. Плотность этого распределения изменяется на всей действительной прямой и задается выражением
1 |
|
expn− |
(x a)2 |
o. |
||
f ( x, a, σ) = |
|
|
|
2−σ2 |
||
p |
|
|
||||
2πσ |
||||||
Как видно из этого выражения, плотность гауссовской случайной величины определяется двумя параметрами — a (математическое ожидание) и σ (стандартное отклонение). Посмотрим, как выглядит плотность этого распределения при различных значениях параметров a и σ. Сначала изобразим плотность стандартного гауссовского закона распределения с параметрами a =0, σ=1. Для этого в электронной таблице нужно создать переменную, которая будет аргументом этой плотности. Поскольку стандартная гауссовская случайная величина с большой вероятностью лежит в интервале (−3, 3), создадим на этом интервале сетку с некоторым шагом, например 0,25. Для этого создадим считающую переменную A, принимающую целые значения от 1 до 25, и из нее получим новую переменную B по формуле B =−3 +0,25 ·( A −1). Значения функции плотности стандартного
§ 4. Нормальное распределение |
189 |
|
|
Рис. 3.32. Выбор функции для вычисления вероятностей стандартного нормального распределения
гауссовского закона можно получить, применив функцию НОРМРАСП, входящую в категорию статистических функций. Для этого поставим курсор на первую ячейку столбца C и, нажав курсором на поле вставки функции fx , вызовем диалог Мастер функций шаг 1 из 2. В поле Категория: выберем значение Статистические. После этого в поле Выберите функцию: выберем функцию НОРМРАСП (см. рис. 3.32).
Нажав на клавишу OK , вызовем диалоговое окно Аргументы функции (см. рис. 3.33), в котором в поле X нужно ввести адрес ячейки аргумента функции плотности (в нашем примере это B1). В поле Среднее введем математическое ожидание (в нашем примере a =0),
Рис. 3.33. Задание параметров для вычисления плотности стандартного нормального закона
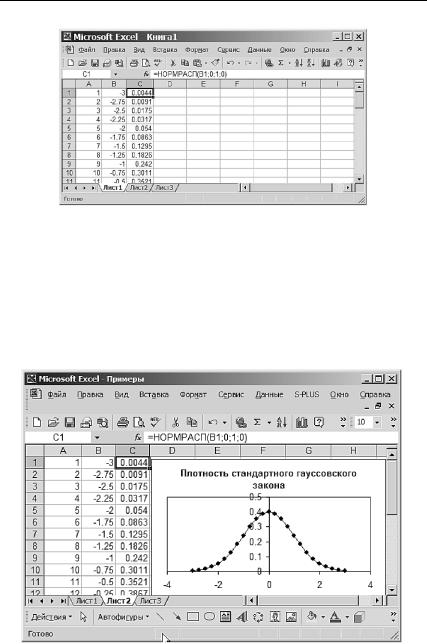
190 Глава 3. Некоторые важные распределения вероятностей
Рис. 3.34. Вычисленные значения плотности стандартного нормального распределения
в поле Стандартное_откл введем σ=1 и в поле Интегральная введем
0 (ЛОЖЬ), что соответствует заданию вычисления плотности распределения. Подтвердив этот выбор, мы получим в ячейке C1 искомое значение функции плотности, которое затем распространим на весь столбец C (см. рис. 3.34). График этой плотности, построенный стандартными средствами EXCEL, изображен на рис. 3.35.
Рис. 3.35. График функции плотности стандартного нормального закона
