
tjurin_teorija_verojatn_978-5-94057-540-5_1
.pdf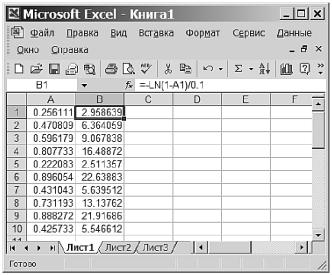
§ 3. Показательное распределение |
171 |
|
|
Рис. 3.22. Сгенерированные 10 равномерно распределенных на [0, 1] и 10 экспоненциально распределенных чисел с параметром распределения λ=0,1
ном распределения. Прежде всего смоделируем последовательность длины 10 равномерно распределенных на [0, 1] случайных величин, вызвав процедуру Генерация случайных чисел (вызывается из Анализ данных меню Сервис). Результат поместим в первые 10 ячеек столбца A. Заполнение полей этой процедуры показано на рис. 3.21.
Затем, поместив курсор в ячейку B1, в поле вставки функции fx введем выражение =-LN(1-A1)/0,1. Распространим его на ячейки B1 − B10, протянув курсор заполнения. Результат моделирования изображен на рис. 3.22.
Обратите внимание на то, что числа получились разные. Среди них есть как значительно меньшие среднего времени 10 лет (2,5 лет), так и значительно превышающие эту величину (22,6 лет).
3.2.2. Вычисление вероятностей. Для предыдущего примера вычислим несколько вероятностей, связанных с экспоненциальным законом распределения.
Пример 3.3.2. Вычислите вероятность того, что холодильник проработает больше:
1) трех лет; 2) пяти лет; 3) семи лет;
4) десяти лет; 5) пятнадцати лет.
172 Глава 3. Некоторые важные распределения вероятностей
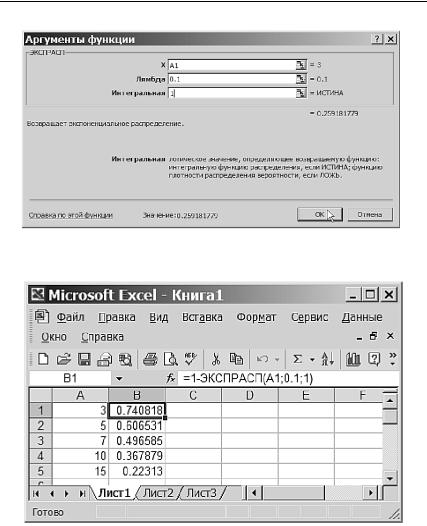
Рис. 3.23. Заполнение полей для ввода аргументов функции ЭКСПРАСП
Рис. 3.24. Вычисление вероятностей вида P( X >x) для экспоненциального распределения с параметром λ=0,1
В EXCEL есть функция ЭКСПРАСП, с помощью которой можно вычислять как плотность экспоненциального распределения λexp(−λx) в точке x, так и функцию распределения F( x, λ) = P( X ¶ x) = 1 − − exp(−λx) в точке x. Функция ЭКСПРАСП входит в группу статистических функций и имеет три аргумента, пример ввода которых
§ 4. Нормальное распределение |
173 |
|
|
приведен на рис. 3.23. Как и для других уже обсуждавшихся функций,
вполе Интегральная для вычисления функции распределения нужно ввести 1 (ИСТИНА), а для вычисления плотности распределения 0
(ЛОЖЬ).
Внашем примере нужно вычислить вероятность P( X > x) = 1 − − F( x, λ), дополнительную к функции распределения. В EXCEL искомые вероятности можно вычислить с использованием функции ЭКСПРАСП следующим образом. Прежде всего подготовим столбец,
вячейках которого (например, A1 −A5) запишем годы, для которых
мы хотим подсчитать вероятность: 3, 5, 7, 10, 15. Поставив курсор в первую ячейку столбца результатов (например, B), в поле вставки функции fx введем выражение = 1−ЭКСПРАСП( A1; 0,1; 1). Затем распространим эту формулу на ячейки столбца B, протащив курсор заполнения до нужной ячейки. Результат вычислений показан на рис. 3.24.
3.3.Задачи
1.В люстре n электрических лампочек. Предположим, что время службы электрической лампочки случайно, распределено показательно и сроки службы отдельных лампочек независимы. Пусть Y — тот промежуток времени, когда все лампочки в люстре горят, после того как перегоревшие ранее лампочки были заменены новыми. Во сколько раз среднее значение Y меньше среднего времени службы отдельной лампочки? (Для ответа сначала найдите распределение величины Y .)
2.К двум кассам супермаркета подошли 3 покупателя со своими многочисленными покупками. Кассиры стали обслуживать первых двух покупателей, а третий стал ждать, пока не освободится одна из касс. Предполагая, что времена обслуживание покупателя независимы и одинаково показательно распределены, найдите:
а) вероятность того, что первой освободится первая касса; б) распределение времени ожидания третьего покупателя;
в) вероятность того, что третий покупатель будет обслужен раньше, чем один из двух первых покупателей.
§4. Нормальное распределение
По-видимому, это наиболее важное распределение вероятностей. Оно появляется в описаниях многих явлений природы, техники и общества. Сам эпитет «нормальное», относимый к этому распределе-

174 Глава 3. Некоторые важные распределения вероятностей
нию, подчеркивает его распространенность. Помимо этого, нормальное распределение играет важную роль в математической теории. Там оно выступает как приближение для многих распределений, возникающих иными путями. Мы уже говорили об этом, обсуждая биномиальное распределение и распределение Пуассона. Более подробно этот разговор будет продолжен в гл. 4.
4.1. Определения и основные свойства
Определение 4.1.1. Распределение вероятностей на числовой прямой называют нормальным (синоним — гауссовским), если оно имеет плотность, которая для каждого x R1 выражается формулой
f ( x) = |
1 |
e− |
(x−a)2 |
(4.1.1) |
|
|
|
2σ2 , |
|||
σp |
|
||||
2π |
|||||
где σ>0 и a — произвольные числа.
Величины a и σ2 (или σ) называют параметрами нормального распределения.
Краткое обозначение для этого распределения — это N(a, σ2 ). Мы пишем X N(a, σ2 ), когда хотим сказать, что случайная величина X имеет нормальное распределение с параметрами a и σ2 .
Нормальное распределение с параметрами a = 0 и σ2 = 1 — т. е.
N(0, 1) — называют стандартным нормальным распределением. Плотность стандартного нормального распределения выглядит проще, чем функция (4.1.1).
Для нее мы примем обозначение ϕ( x):
ϕ( x) = p |
1 |
e− |
x2 |
. |
(4.1.2) |
2 |
|||||
|
2π |
|
|||
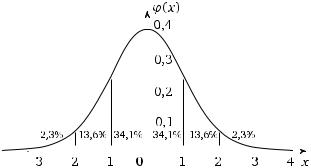
График функции y =ϕ( x) — симметричная колоколообразная кривая, изображенная на рис. 3.25. (На этом рисунке для осей x и y ис-
1 |
|
|
пользованы разные масштабы. Максимум функции ϕ( x) равен p |
|
≈ |
2π |
||
≈0,399, так что при одинаковых масштабах график был бы более пологим.)
Можно показать, что площадь, ограниченная кривой y = ϕ( x) и осью абсцисс, равна 1, т. е. что
Z+∞
p |
1 |
e− |
x2 |
dx = 1. |
(4.1.3) |
2 |
|||||
|
2π |
|
|
||
−∞
Мы принимаем этот факт без доказательства.
|
|
|
|
|
|
|
|
§ 4. Нормальное распределение |
175 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.25. Плотность стандартного нормального распределения N(0, 1)
С возрастанием |x|плотность ϕ( x) быстро убывает. Поэтому вероятность концентрируется около начала координат. Так, на интервал (−2, 2) приходится вероятность 0,956, а на интервал (−3, 3) — вероятность, равная 0,997. Отсюда следует, в частности, что за пределами интервала (−3, 3) остается весьма малая вероятность 0,003 (более точное значение 0,0027). На рис. 3.25 показано примерное распределение долей вероятностей (в процентах) между единичными интервалами около начала координат. Так, на интервал (0, 1) приходится вероятность, равная примерно 0,341, а на интервал (1, 2) — 0,136.
Случайную величину, имеющую стандартное нормальное распределение N(0, 1), традиционно обозначают через Z. Для Z указанные выше вероятности становятся вероятностями событий:
P(−2 < Z < 2) = 0,956, |
(4.1.4) |
P(−3 < Z < 3) = 0,997, |
|
P(0 < Z < 1) = 0,341. |
|
Связь стандартного и произвольного нормального распределений.
Связь стандартного и произвольного нормальных распределений проста. Пусть Z обозначает случайную величину с плотностью (4.1.2). Рассмотрим новую случайную величину X, которую случайная величина Z порождает соотношением
X = a +σZ. |
(4.1.5) |
Теорема. Плотность случайной величины (4.1.5) выражается формулой (4.1.1). Другими словами, линейное преобразование (4.1.5)
стандартной нормальной случайной величины Z приводит к слу-

176 Глава 3. Некоторые важные распределения вероятностей
чайной величине X = a + σZ, имеющей нормальное распределение вероятностей N(a, σ2 ) с параметрами a и σ2 .
Доказательство этого утверждения просто. Надо лишь вспомнить, что такое плотность вероятности и плотность случайной величины. Рассмотрим некоторую окрестность точки x, x R1 , и вероятность, приходящуюся на эту окрестность. Плотность вероятности в точке x — это тот множитель, на который надо умножить размер упомянутой окрестности, чтобы получить (приближенное) значение ее вероятности. Для случайной величины X и ее плотности f ( x) точный смысл этого напоминания означает, что для малого h > 0 выполняется равенство
P( x < X < x +h) = f ( x)h +o(h).
(Вероятность, причитающаяся интервалу ( x, x +h), есть вероятность события ( x < X < x + h).) Заместим величину X в этой формуле её выражением (4.1.5) через Z и преобразуем формулу обсуждаемого события:
P( x < a +σZ < x +h) = P x σ−a < Z < x σ−a + σh .
Еще раз применив определение плотности, теперь для случайной величины Z, получим, что
f ( x)h +o(h) = ϕ x −σa σh + o(σh) .
Разделим правую и левую часть полученного равенства на h и перейдем к пределу при h →0. Учитывая, что предел функции o(h)/h равен 0, получаем
f ( x) |
|
1 |
ϕ |
x −a |
|
|
1 |
|
− |
(x−a)2 |
, |
(4.1.6) |
|
= |
= |
|
2σ2 |
||||||||||
|
|
|
|
||||||||||
|
σ |
σ |
σp2πe |
|
|
||||||||
что и требовалось.
Замечание. Интервал ( x, x +h) был взят только ради определенности. С тем же результатом (4.1.6) мы могли бы рассмотреть интервал ( x −h, x) или любой интервал вида ( x −h1, x +h2), где h1, h2 >0
и h1 +h2 =h.
Следствие 1. Пусть X N(a, σ2 ). Тогда случайная величина Xσ−aN(0, 1), т. е. от нормальной случайной величины X с произвольными параметрами a и σ2 >0 всегда можно перейти к стандартной нормальной случайной величине Z N(0, 1). Эта процедура называется стандартизацией. Она играет важную роль при вычислении вероятностей тех или иных событий, связанных с произвольным нормаль-
ным распределением, а так же при доказательстве ряда теорем.

§ 4. Нормальное распределение |
177 |
|
|
Следствие 2. Линейные функции от нормальных случайных величин распределены нормально.
Более определенно: пусть X — случайная величина, распределенная по некоторому нормальному закону; пусть Y =c +dX, где c и d — произвольные числа. Тогда распределение случайной величины Y тоже нормальное.
Действительно, согласно следствию 1 случайную величину XN(a, σ2 ) можно представить в виде линейной комбинации от стандартной нормальной случайной величины:
X = a +σZ.
Следовательно,
Y= c +dX = c +d(a +σZ) = (c +da) +dσZ,
исогласно теореме имеет нормальное распределение.
Правило трех сигм. Концентрация значений нормальной случайной величины около значения a свойственна любому распределению
N(a, σ2 ). Пусть X N(a, σ2 ). Рассмотрим Z = X σ−a . Как мы знаем, Z N(0, 1). Согласно (4.1.4) имеем P(|Z|<3) =0,997. Учитывая, что X σ−a =Z, получаем
P(|X −a| < 3σ) = 0,997,
или
P(a −3σ < X < a +3σ) = 0,997.
Это свойство нормального распределения иногда называют «правилом трех сигм»: практически вся нормальная вероятность располагается не далее чем на расстоянии 3σ от своего центра.
Для плотности ϕ( x) (4.1.2) стандартного нормального распределения составлены подробные таблицы. Их можно найти в сборниках таблиц по математической статистике. С помощью таких таблиц и формулы (4.1.6) можно с требуемой точностью вычислять значения любых нормальных плотностей — если понадобится.
Функция распределения и функция квантилей. Напомним, что функцией распределения F( x) случайной величины X называют функцию переменного x R1, определенную как
F( x) = P( X ¶ x).
Если случайная величина X имеет плотность f ( x), то
Zx
F( x) = f (u) du.
∞
178 Глава 3. Некоторые важные распределения вероятностей
Интеграл в правой части здесь рассматривается как функция своего верхнего предела интегрирования x. Чтобы подчеркнуть это лишний раз, мы под знаком интеграла используем другую переменную u,
−∞ <u ¶x.
Для стандартной нормальной плотности ϕ( x) и стандартного нормального распределения эта формула определяет функцию стандартного нормального распределения
x |
|
|
|
|
|
|
Φ( x) = Z |
1 |
e− |
u2 |
|
(4.1.7) |
|
p |
|
2 du. |
||||
2π |
||||||
−∞
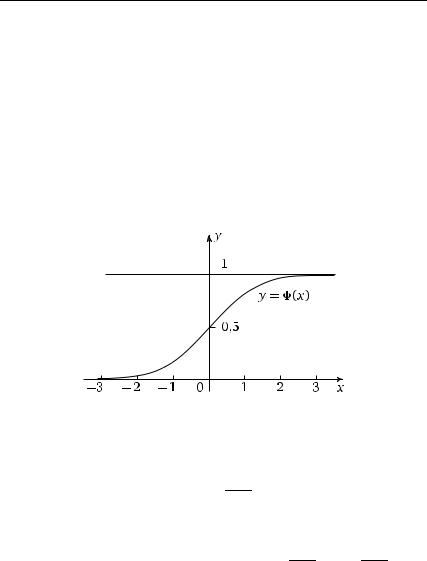
График функции y =Φ( x) изображен на рис. 3.26.
Рис. 3.26. Функция распределения стандартного нормального распределения N(0, 1)
Функция распределения произвольного нормального распределения N(a, σ2 ) выражается через функцию Φ( x) следующим образом:
F( x) = Φ |
x σ−a |
. |
(4.1.8) |
Доказательство основано на формуле (4.1.5), которая связывает распределение N(a, σ2 ) со стандартным распределением N(0, 1):
F( x) |
|
P( X |
|
x) |
|
P(a |
|
σZ |
|
x) |
|
P Z |
|
σ |
|
|
σ |
. |
|
= |
|
¶ |
|
= |
|
+ |
|
¶ |
|
= |
|
¶ |
x −a |
|
= Φ |
x −a |
|
Для функции Φ( x) стандартного нормального распределения составлены подробные таблицы. Их можно найти в сборниках статистических таблиц. В пакетах статистических программ есть команды, по которым компьютер с необходимой точностью вычисляет Φ( x) для назначенного x. Небольшая таблица функции нормального распределения приведена на с. 253.
§ 4. Нормальное распределение |
179 |
|
|
Соотношение (4.1.7) позволяет с помощью таблицы стандартной функции распределения вычислять с необходимой точностью функцию любого нормального распределения, если параметры этого распределения заданы.
Рис. 3.27. Функция квантилей стандартного нормального распределения N(0, 1)
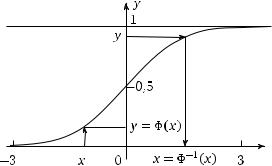
Подробные таблицы составлены и для функции, обратной к функции y =Φ( x). Эта обратная функция показана на рис. 3.27. Связь прямой и обратной функций легко понять из рис. 3.26. На этом рисунке изображен график функции y =Φ( x). Стрелками изображены переходы от значений x к значениям y и от значений y к значениям x. Когда мы по стрелкам идем от x к y, мы по заданному значению x получаем значение y =Φ( x). Это прямая функция. Когда мы по стрелкам (другим) идем от y к x, мы по заданному значению y получаем значение обратной функции x =Φ−1( y).
На рис. 3.27 видно, что обратная функция Φ−1(·) определена на интервале (0, 1) и что значения функции Φ−1 (·) пробегают всю числовую прямую.
Если захотите увидеть график обратной функции в традиционном изображении, когда значения аргумента отложены на горизонтальной оси, а значения функции — на вертикальной оси, рассмотрите рис. 3.26 «на просвет», с тыльной стороны листа. (Рассмотрите лист так, чтобы на горизонтальной оси точка 0 располагалась левее точки 1.)
Если прямая функция — это функция распределения, то обратную к ней функцию называют функцией квантилей. В данном случае Φ−1(·) — это функция квантилей стандартного нормального распределения N(0, 1).

180 Глава 3. Некоторые важные распределения вероятностей
Понятие квантили в равной степени относится и к случайной величине, и к ее функции распределения.
Определение 4.1.2. Пусть X — случайная величина, F( x) =P( X ¶ ¶x) — ее функция распределения. Предположим, что функция y =F( x) непрерывна и монотонно возрастает с ростом x. Пусть p (0, 1). Квантилью (точнее p-квантилью) случайной величины X и p-квантилью ее распределения называют такое число x, что
P( X ¶ x) = p.
Можно сказать иначе: p-квантиль — это решение относительно x уравнения
F( x) = p,
т. е. нам необходимо по заданному значению p найти такое x, что F( x) = p. Часто p-квантиль обозначают xp. При сделанных выше предположениях о F( x) квантили существуют для любого p (0, 1) и определяются однозначно.
Зная функцию квантилей стандартного нормального распределения N(0, 1), мы без труда находим квантили любого нормального распределения N(a, σ2 ) при заданных a и σ. В силу соотношения (4.1.8) уравнение для квантилей распределения N(a, σ2 ) имеет вид
Φ |
|
x −a |
|
= |
p, |
|
откуда следует, что |
σ |
|
|
|||
xp = a +σΦ−1 ( p). |
(4.1.9) |
|||||
Нахождение p-квантилей как для нормального распределения, так и для других распределений играет важную роль в математической статистике в процедурах принятия решений. При этом величина p выбирается обычно близкой к 1, скажем 0,95 или 0,99. По смыслу величина p интерпретируется как уровень доверия или надежность принятого решения. Поэтому p и стремятся выбрать поближе к единице. Последняя означает полное доверие, или 100% надежность. Однако когда нам приходится принимать решения или делать выводы по изменчивым, неточным, случайным данным, то требование стопроцентной надежности вывода приводит к слишком общим и практически бесполезным заключениям. (Виновата в подобном положении дел именно случайность.)
Упражнения
Втаблице 3.1 приведены значения функции Φ( x) для некоторых x с точностью до четвертого знака после запятой. Используя таблицу и свойства плотности стандартного нормального распределения,
