
tjurin_teorija_verojatn_978-5-94057-540-5_1
.pdf§ 1. Случайные величины и их распределения |
91 |
|
|
прос начисляется нуль, один или два балла в зависимости от того, насколько он отражает тестируемое свойство. Итоговый показатель теста X — сумма баллов, набранная за ответы на все вопросы. Укажите множество возможных значений этой случайной величины. Предположим дополнительно, что ответы на каждый вопрос выбираются случайным образом и независимо.
а) Укажите вероятность того, что X примет свое максимальное значение.
б) Укажите вероятность того, что X =9. Сколько элементарных исходов этого эксперимента приводят к этому значению случайной величины?
1.3. Непрерывные случайные величины
Не все случайные величины являются дискретными. У многих случайных величин совокупности возможных значений образуют непрерывные множества. Например, время службы электрической лампочки может, в принципе, принимать любое значение от нуля до бесконечности (как хорошо известно, это непрерывное множество не является счетным). И если лампочка исправна, то равна нулю вероятность того, что время ее службы будет в точности равно какому-либо определенному, заранее выбранному значению. Ненулевыми будут вероятности только сложных событий: например, что время службы лампочки — от 500 до 800 часов или время службы менее 1000 часов и т. д. Для подобных случайных величин мы не можем задать их распределений, просто указывая вероятность каждого возможного значения. (Все эти вероятности равны нулю.) При описании таких случайных величин используют другие средства. Часто такое распределение вероятностей можно задать с помощью плотности вероятности. О плотности вероятности мы уже говорили в п. 2.1 гл. 1, когда обсуждали распределение вероятностей по непрерывным совокупностям элементарных исходов.
Пусть X = f (ω) — некоторая случайная величина, т. е. функция от случайного исхода ω, ω Ω. Пусть значения этой случайной величины X пробегают отрезок числовой прямой или всю прямую. С помощью функции X = f (ω) распределение вероятностей, существующее на множестве Ω, переносится на числовую прямую. Часто (не всегда) возникающее на этой прямой распределение вероятностей можно описать с помощью функции плотности. Эту плотность связывают с X: говорят, что это плотность случайной величины X. Пусть t пробегает значения на числовой прямой.

92 |
Глава 2. Случайные величины |
|
|
Определение 1.3.1. Функцию p(t) называют плотностью вероятности в точке t (иногда — плотностью случайной величины X), если для любых чисел a, b (пусть a <b) выполняется равенство
Zb
P(a < X < b) = p(t) dt.
a
Заметим, что если у случайной величины X есть плотность, то вероятности событий (a < X <b), (a ¶X <b), (a < X ¶b), (a ¶X ¶b) одинаковы, так как вероятность того, что непрерывная случайная величина примет конкретное значение (или X =b) X =a — это всегда равна нулю.
Иногда, чтобы подчеркнуть, что p(t) плотность вероятности случайной величины X, пишут pX (t).
Определению 1.3.1 можно дать иную, дифференциальную форму. В этой форме связь между вероятностью и плотностью становится особенно ясной.
Определение 1.3.2. Функцию pX (t) называют плотностью случайной величины X, если для любого1 переменного h >0 и любого t на числовой прямой справедливо равенство
P(t < X < t +h) = pX (t)h +o(h),
где o(h) — малая (точнее, бесконечно малая) по сравнению с h величина.
Наглядное содержание второго из этих определений состоит в том, что вероятность, приходящаяся на малый отрезок, оказывается приблизительно пропорциональной длине этого отрезка, причем коэффициент пропорциональности равен значению функции плотности вероятности в некоторой точке этого отрезка. В виде математической формулы сказанное можно записать так:
P(t < X < t +h) ≈ p(t)h,
когда h >0 — малое число.
Свойства функции плотности вероятностей. Отметим простые свойства функций плотности, используемые на практике.
1 Если говорить точно — любого, за исключением множества меры нуль. Предыдущее (интегральное) определение показывает, что функция плотности может быть произвольно изменена на любом множестве нулевой меры, все равно удовлетворяя определению. Практически, разумеется, используют наиболее регулярную и простую из возможных функций плотности.

§ 1. Случайные величины и их распределения |
93 |
|
|
1.Функция плотности неотрицательна1: p(t) ¾0 для любого t.
2.Интеграл от функции плотности по всей числовой прямой равен единице:
Z+∞
p(t) dt = 1.
−∞
Первое из этих свойств следует из того, что вероятность любого события неотрицательна, а второе — из того, что вероятность достоверного события, т. е. события, состоящее в том, что случайная величина просто примет какое-то любое свое возможное значение на числовой прямой, равна по определению единице.
Определение 1.3.3. Распределение вероятностей, которое можно задать с помощью функции плотности, называют непрерывным. Часто непрерывной называют и случайную величину, если у нее есть функция плотности.
Для непрерывного распределения вероятность каждого отдельного значения случайной величины равна нулю. На этом основано противопоставление непрерывных и дискретных распределений. Для последних полная, единичная вероятность распределена конечными положительными порциями. Для непрерывных же она как бы «разлита» по области значений случайной величины (в данном случае — по числовой прямой).
Приведем некоторые примеры.
Пример 1. Выше мы упомянули как пример непрерывной случайной величины время службы электрической лампочки. В более широком плане можно говорить о случайном времени безотказной работы любого прибора или изделия. Хорошая математическая модель для плотности таких случайных величин — так называемая показательная, или экспоненциальная, плотность:
|
θ1 e− |
t |
для t ¾0; |
|
p(t, θ) = |
θ |
|||
|
|
0 |
|
для t < 0, |
|
|
|
||
где θ >0 — параметр распределения. (О вероятностном смысле этого параметра можно будет говорить позже.) «Хорошая» в данном случае
1 Более строго, надо сказать, что она неотрицательна на любом подмножестве числовой прямой ненулевой меры. Однако чтобы не прибегать к более сложным математическим конструкциям и теории меры, мы употребляем нестрогое выражение «используемые на практике».

94 |
Глава 2. Случайные величины |
|
|
означает: математически удобная и дающая практически правильные результаты; слово же «модель» подчеркивает лишь приблизительную правильность принимаемой формулы. Об экспоненциальном (показательном) распределении на числовой прямой мы уже говорили в п. 2.1 гл. 1. Там же на рис. 1.16 был приведен график функции p(t, θ). Говоря сейчас о распределении случайной величины X, по сути мы говорим о том же распределении, так как эту случайную величину можно рассматривать как тождественную. Более подробно о свойствах этого распределения речь пойдет в § 3 гл. 3.
Вероятность того, что случайная величина X с показательным распределением вероятностей примет значение на отрезке [a, b], согласно определению есть
Zb
P(a ¶ X ¶ b) = θ1 e−θt dt = e−θa −e−θb .
a
При a =b, очевидно, величина в правой части этого выражения равна нулю. Другими словами, P( X =a) =0.
Пример 2. Другой пример — так называемое равномерное распределение. Пусть [a, b] — произвольный отрезок числовой прямой, a < b. Распределение вероятностей называют равномерным на отрезке [a, b], если плотность этого распределения p(t) постоянна для t [a, b] и равна нулю для всех остальных значений t. Вспомнив, что интеграл от p(t) по всей числовой прямой равен 1, найдем, что
упомянутое постоянное на [a, b] значение плотности равно b −1 a .
С помощью математических формул сказанное выше можно записать так:
|
|
0 |
1 |
для t < a; |
|
|
|
|
|
|
|
p(t) = |
|
b −a |
для a ¶t ¶ b; |
||
|
|
|
|
|
|
|
|
0 |
|
для t > b. |
|
|
|
|
|||
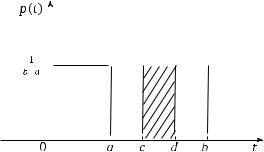
График плотности равномерного распределения на отрезке [a, b] приведен на рис. 2.1.
Вычисление вероятности того, что случайная величина примет значение в каком-то интервале (c, d) (d >c) отрезка [a, b], в данном случае вычисляется как площадь прямоугольника с основанием (c, d)
и высотой b −1 a , т. е.
P(c < X < d) = bd−−ac .
|
§ 1. Случайные величины и их распределения |
95 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.1. График плотности равномерного распределения на отрезке [a, b]
Вэтом можно убедиться, вычислив совсем простой интеграл от постоянной на отрезке [a, b] плотности равномерного распределения.
Вспоминая пример 2 из п. 1.1, мы можем сказать, что равномерное распределение на [a, b] описывает равновозможный случайный выбор точки из [a, b]. Равномерно распределенные случайные величины часто используют, чтобы описать ошибки, возникающие при округлении (при записи чисел с ограниченным числом знаков).
Как правило, для приложений достаточно двух вышеописанных типов распределений — дискретного и непрерывного (точнее, имеющего плотность). Хотя можно встретиться с распределениями, представляющими собой смесь двух этих типов, и даже с более сложными.
Вгл. 3 мы подробнее познакомимся с некоторыми важными для приложений случайными величинами и их распределениями.
Упражнения
1. Случайный эксперимент заключается в случайном выборе точки внутри круга радиуса R (предполагается, раз речь идет о случайном выборе, что вероятность попасть в любую замкнутую область круга пропорциональна площади этой области). Определим случайную величину X как расстояние от выбранной точки до центра круга.
а) Какие значения может принимать случайная величина X? б) Вычислите P( X <r), где 0 <r <R.
в) Чему равна плотность распределения этой случайной величины?
1.4. Функции распределения
Выше отмечалось, что дискретная случайная величина исчерпывающе описывается рядом распределения, а непрерывная — плотно-

96 Глава 2. Случайные величины
стью распределения вероятностей, и говорилось, чем вызвано подобное различие. Однако для описания вероятностных распределений на числовой прямой есть также средство, одинаково пригодное как для непрерывных, так и для дискретных и вообще для любых случайных величин. Это функция распределения вероятностей, или просто функция распределения.
Пусть X обозначает случайную величину, принимающую значения на числовой прямой, а x — (числовая) переменная на этой прямой.
Определение 1.4.1. Для любого x R1 функцией распределения F( x) случайной величины X называют F( x) = P( X ¶x), т. е. вероятность того, что случайная величина не превысит значение x.
Иногда, чтобы подчеркнуть связь функции распределения F( x) со случайной величиной X, пишут FX ( x).
Согласно определению функция распределения FX ( x) определена на всей числовой прямой, вне зависимости от того, какие значения принимает порождающая ее случайная величина.
Для дискретной случайной величины X вычисление функции FX ( x) в произвольной точке x сводится к следующему. Надо просуммировать вероятности всех тех значений случайной величины X, не превосходящее x. Если таких значений не окажется, т. е. случайная величина не может принять значение не превосходят x, очевидно, FX ( x) =0 как вероятность невозможного события. Обратно, если все возможные значения случайной величины не превосходят x, то, очевидно, FX ( x) =1 как вероятность достоверного события. Например, если случайная величина X — число очков, выпавших при броске игральной кости, то
FX (−125) = FX (−0,5) = FX (0) = FX (0,9) = 0,
так как все указанные значения (x = −125, x = −0,5, x = 0, x = 0,9) меньше 1 — минимального значения этой случайной величины. Точно так же
FX (6) = FX (6,5) = FX (7) = FX (110,9) = 1.
Исходя из описанного правила вычисления функции распределения ее иногда именуют функцией накопленной вероятности.
Для непрерывной случайной величины X вычисление функции FX ( x) в произвольной точке x сводится к вычислению интеграла от плотности распределения случайной величины p(t):
Zx
FX ( x) = p(t) dt.
−∞

§ 1. Случайные величины и их распределения |
97 |
|
|
Обратим внимание на то, что здесь мы рассматриваем интеграл как функцию верхнего предела. По смыслу интеграла значение функции распределения FX ( x) в точке x есть просто площадь фигуры, заключенной между графиком плотности p(t), осью абсцисс и вертикальной прямой, проходящей через точку x, как это показано на рис. 2.2.
Рис. 2.2. Графический смысл функции распределения непрерывной случайной величины
Поэтому, говоря о вероятностях событий, связанных с непрерывной случайной величиной, мы просто оперируем площадями под графиком плотности. В большинстве практических приложений нет необходимости, а иногда и возможности, вычислять вручную интегралы от функций плотности. Об этом мы еще скажем подробнее.
Свойства функции распределения. Перечислим ряд простых свойств любой функции распределения.
1.Функция F( x) монотонно возрастает с ростом x (точнее сказать, не убывает, потому что могут существовать участки, на которых она постоянна) от значения 0 до значения 1.
Действительно, пусть x1 < x2. Покажем, что F( x1) ¶ F( x2). Обозначим через A событие (т. е. подмножество элементарных исходов) ( X ¶x1), а через B — событие ( X ¶x2). Ясно, что все элементарные исходы события A принадлежат событию B, так как если X = f (ω) ¶x1, то очевидно, что при этом X ¶ x2. По свойству вероятности собы-
тий из того, что A B следует, что P( A) ¶ P(B). Но P( A) = F( x1), а P(B) = F( x2). Отсюда получаем F( x1) ¶ F( x2), что и требовалось
доказать.
2. Очевидно, что 0 ¶F( x) ¶1 для любого x. При этом F( x) →0 при x →−∞ и F( x) →1 при x →∞. Здесь просто идет речь о практически невозможных и достоверных событиях.

98 |
Глава 2. Случайные величины |
|
|
3.У непрерывной случайной величины X функция распределения непрерывная. С помощью плотности pX (t) она выражается в виде
интеграла: Zx
FX ( x) = pX (t) dt.
−∞
А интеграл как функция от верхнего предела интегрирования непрерывен.
На следующих ниже рисунках изображены графики функций показательного (рис. 2.3 a)) и равномерного (рис. 2.3 б)) распределений.
а) |
б) |
Рис. 2.3. Графики функции распределения: a) показательного распределения вероятностей; б) равномерного распределения вероятностей
4.У дискретной случайной величины функция распределения ступенчатая, она возрастает скачками в тех точках, вероятности которых положительны. Это точки разрыва функции F( x).
На рис. 2.4 приведен график функции распределения для описанной выше случайной величины — суммы очков, выпавших при дву-
Рис. 2.4. График функции распределения суммы очков, выпавших при двукратном бросании игральной кости
§ 1. Случайные величины и их распределения |
99 |
|
|
кратном бросании игральной кости. При этом величины скачков равны вероятностям соответствующих значений этой случайной величины. (Ряд распределения этой случайной величины приведен в таблице 2.4.)
Примеры.
1. Пусть случайная величина X может принимать только значения 0 и 1 с вероятностями p и 1 −p соответственно (причем 0 ¶p ¶1). В этом случае функция распреде-
ления имеет вид |
|
|
|
если x < 0; |
|
|
0, |
|
|
F( x) = p, |
если 0 ¶ x < 1; |
|
1, |
если x ¾1. |
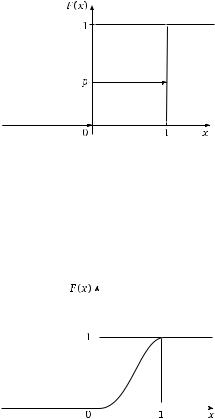
График этой функции изображен на рис. 2.5.
Рис. 2.5. График функции распределения, сосредоточенного в двух точках: 0 и 1
2. Пусть функция плотности p(t) равна
|
|
0, |
|
|
|
если t < 0; |
|
p(t) = |
6t(1 |
− |
t), |
если 0 ¶ t < 1; |
|||
|
|
|
|
|
|
||
|
0, |
|
если t ¾1. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2.6. Пример непрерывной функции распределения: 0 и 1

100 Глава 2. Случайные величины
+R∞
(Легко проверить, что в данном случае p(t) dt =1 и p(t) ¾0, так что функция p(t)
−∞
может быть плотностью случайной величины.) Функция распределения при этом равна |
|||||
F( x) = |
|
0 |
3 + 2 |
для x ¶ 0;¶ |
|
|
|
|
|
|
¶ |
|
−2x |
3x |
для 0 |
¾ x 1; |
|
|
|
1 |
|
для x |
1. |
Ее график приведен на рис. 2.6.
Приведенные примеры иллюстрируют указанные выше свойства функций распределения.
5.Если в точке x функция распределения y =F( x) имеет скачок, то величина этого скачка равна вероятности, сосредоточенной в точке x, т. е. вероятности события ( X = x). Если же точка x — точка непрерывности функции y = F( x) и, более того, F( x) имеет производную в этой точке, то график функции F( x) в точке x имеет касательную, тангенс угла наклона которой равен плотности p( x) в этой точке, т. е. плотность вероятности p(t) есть производная от функции распределения F( x) при x =t:
p(t) = |
dF(x) |
|
= F′( x) при x = t. |
|
dx |
||||
|
|
|||
Заметим, что даже в самых простых случаях (см. примеры функций распределения на рис. 2.3) непрерывные функции распределения могут быть не дифференцируемы в некоторых точках. Для показательного распределения это точка x =0, а для равномерного распределения на отрезке [a, b] это точки x =a и x =b.
6.Функции распределения как дискретных, так и непрерывных случайных величин позволяют легко вычислять вероятности попадания случайных величин в заданный интервал (a, b). Действительно
P(a < X ¶ b) = F(b) −F(a). |
(1.4.1) |
Однако для практически важных случайных величин часто совсем не просто бывает вычислить непосредственно, вручную, значения самих функций распределения. Это связно с тем, что для ряда плотностей непрерывных распределений, распространенных на практике, не удается в явном виде вычислить соответствующий интеграл от плотности вероятности или это вычисление трудоемко. В частности, это относится к нормальному распределению вероятностей. Аналогичная проблема существует и для распределений важных дискретных случайных величин, например для распределения числа успехов в n испытаниях Бернулли, когда n превышает несколько десятков.
