
tjurin_teorija_verojatn_978-5-94057-540-5_1
.pdf§ 2. Вероятности случайных событий |
31 |
|
|
объема, температуры, времени и т. п. К использованию модели непрерывных пространств часто прибегают и в социально-экономической практике, обсуждая объемы добычи полезных ископаемых и производства массовых изделий, годовые доходы, цены на продукты, различные демографические показатели, и т. п. Переход от формально дискретных пространств к непрерывным в теории вероятностей часто связан и с тем, что задание вероятностей в последних оказывается гораздо проще и компактней с практической точки зрения, а возникающие при переходе погрешности не велики.
В непрерывных пространствах основой для определения вероятностей событий служит плотность вероятности.
Пусть для определенности Ω— это числовая прямая R1 . События A в этом случае — это области (подмножества) числовой прямой (отрезки, интервалы и их комбинации и т. п.). Произвольный элементарный исход — точку на числовой прямой — обозначим на этот раз через x, x R1 (вместо общего обозначения ω, ω Ω).
Определение 2.1.2. Плотностью вероятности называют функцию f ( x), заданную для всех x R1 и такую, что
f ( x) ¾0 для всех x R1 , |
(2.1.1) |
Z+∞ f ( x) dx = 1. |
(2.1.2) |
−∞
Если известно, что Ω— это некоторая область в R1 , то полагают
f ( x) = 0 для x не принадлежащих Ω. |
(2.1.3) |
Значение f ( x) для конкретного x называют плотностью вероятности
вточке x.
Спомощью плотности вероятности определяют вероятность произвольного события A.
Определение 2.1.3. Вероятность P( A) события A есть |
|
|
P( A) = Z |
f ( x) dx. |
(2.1.4) |
A
Поясним, как надо понимать интегрирование по заданному множеству A в формуле (2.1.4). Если A R1 — это отрезок, A =[a, b], то
Z |
Zb |
(2.1.5) |
f ( x) dx = |
f ( x) dx. |
Aa

32 |
Глава 1. Основы теории вероятностей |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.14. Задание вероятности с помощью плотности
Если A — это объединение непересекающихся отрезков [a, b] и [c, d],
то |
Z |
b |
d |
|
|
f ( x) dx = Z |
f ( x) dx +Z |
f ( x) dx и т. д. |
|
|
A |
a |
c |
|
С геометрической точки зрения интеграл в правой части равенства (2.1.4) — это площадь под кривой y = f ( x), расположенная над множеством A. На рис. 1.14 эта площадь выделена штриховкой.
Для множества A, если оно представляет собой объединение
конечного числа отрезков, интервалов, полуинтервалов (в том числе |
|
и неограниченных), определение RA |
f ( x) dx очевидно. С геометриче- |
ской точки зрения такой интеграл — все та же площадь между кривой y = f ( x) и множеством A на оси абсцисс.
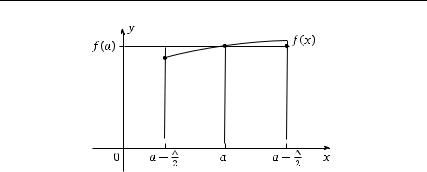
Формула (2.1.4), задающая вероятность события с помощью плотности вероятности f ( x), позволяет прояснить смысл функции f ( x). Рассмотрим произвольную точку a на числовой прямой. На практике значение a обычно является результатом измерения. Однако следует помнить, что наши измерения, как правило, неточны, приблизительны. Так, говоря, что рост человека равен 175 см., мы подразумеваем, что величина его роста примерно равна этому числу и более высокая точность нам не требуется. Другими словами, говоря, что результат измерения равен a, мы на самом деле подразумеваем, что он попал в интервал (a − /2, a + /2), где — цена деления используемой шкалы измерения. (При измерении роста в сантиметрах Δ=1 см.)
Рассмотрим событие A, представляющее интервал (a − /2, a + +Δ/2). Согласно определению вероятность события A есть
a+ΔZ/2
P( A) = f ( x) dx.
a− /2
§ 2. Вероятности случайных событий |
33 |
Рис. 1.15. Связь плотности вероятности в точке a с веро- |
|
ятностью попасть в окрестность этой точки |
|
Предположим, что функция плотности f ( x) непрерывна в точке a и величина невелика. Тогда по свойствам интеграла
a+ΔZ/2
P( A) = f ( x) dx ≈ f (a) . (2.1.6)
a− /2
Геометрически это примерное равенство означает, что площадь под кривой плотности f ( x) над интервалом (a − /2, a +Δ/2) примерно равна площади прямоугольника с основанием (a − /2, a +Δ/2) и высотой f (a) (см. рис. 1.15). Это же рассуждение используется в математическом анализе, когда осуществляется переход от интегральных сумм по малым интервалам к интегралу.
Итак, выражение (2.1.6) говорит, что вероятность оказаться в окрестности точки a (попасть в интервал (a − /2, a +Δ/2)) примерно прямо пропорциональна величине плотности вероятности f (a) в точке a. Чем больше значение f (a), тем больше вероятность. Обсуждение этого вопроса мы продолжим чуть позже.
Упомянутые выше свойства плотности вероятности (2.1.1) и (2.1.2) обеспечивают для вероятностей событий свойства (2.0.1) и (2.0.2).
Расширение операции интегрирования на более сложно устроенные множества A, A R1 , составляет содержание теории интегрирования по Лебегу. Такая теория нужна для создания математически завершенной теории вероятностей. По счастью, нам нет нужды углубляться в эти математические вопросы: этого не требуют статистические (практические) задачи, являющиеся целью данной книги. Нам будет достаточно простых средств из классического математического анализа: интеграла Римана, формулы Ньютона—Лейбница, рядов и т. п.
34 |
Глава 1. Основы теории вероятностей |
|
|
Примеры
1. Экспоненциальная плотность.
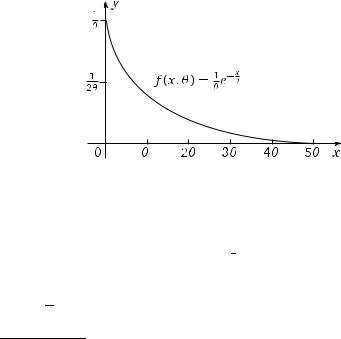
В приложениях теории вероятностей, имеющих дело со случайными явлениями типа времени ожидания отказа (поломки), времени обслуживания клиента в банке или покупателя в магазине, продолжительности телефонного разговора или разгрузки корабля в порту и т. д. в качестве плотности вероятности часто используют функцию
|
θ1 e− |
x |
для x ¾0; |
||
f ( x, θ) = |
θ |
||||
|
|
|
|
1 |
|
|
|
0 |
|
для x < |
0. |
Здесь θ > 0 (читается «тэта») — параметр . Забегая вперед, скажем, что по смыслу θ — среднее время службы изделия, среднее время обслуживания и т. п.
График функции f ( x, θ) представлен на рис. 1.16.
Рис. 1.16. Плотность вероятности показательного распеределения
Легко видеть, что f ( x, θ) ¾0 для любого θ >0 и что
Z∞ Z∞ Z∞ Z∞
f ( x, θ) dx = f ( x, θ) dx = θ1 e−θx dx = e−t dt = −e−∞ +e0 = 1,
−∞ |
0 |
0 |
0 |
где t = θx . Таким образом, требования из определения плотности вероятности (2.1.1) и (2.1.2) выполняются.
1 Параметрами называют переменные величины, значения которых в каждой отдельной задаче сохраняются постоянными.
§ 2. Вероятности случайных событий |
35 |
|
|
Плотность вероятности f ( x, θ) называют показательной или экспоненциальной. Подробнее о ней будет рассказано ниже, в гл. 3. Но уже сейчас из графика функции плотности (рис. 1.16) можно заметить, что вероятность события A, состоящего в том, что изделие прослужит в три раза дольше, чем среднее время службы, невелика. Действительно, ведь эта величина есть площадь под графиком плотности на интервале (3θ, ∞).
2. Нормальная плотность.
Статистические свойства (изменчивость) многих явлений характеризует плотность вероятности, называемая нормальной. Само название подчеркивает распространенность и ожидаемость этого распределения вероятностей. Нормальная плотность хорошо описывает различные изменчивые социально-экономические характеристики, метрические характеристики людей, животных и растений одного вида, статистические свойства ошибок измерения. Эта же плотность часто выступает как предельная при изучении законов изменчивости сумм случайных величин. Об этой роли нормального распределения мы подробно будем говорить в гл. 4.
Плотность нормального распределения на прямой содержит в своей формуле два параметра (a R1 и σ>0):
f ( x, a, σ) = |
1 |
exp − |
(x2−σa2 )2 |
|
для x R1. |
|
σp |
|
|||||
2π |
||||||
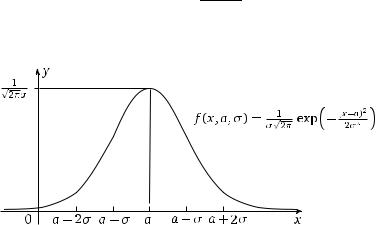
График плотности нормального распределения представлен на рис. 1.17.
Рис. 1.17. Плотность нормального распределения
Очевидно, что
f ( x, a, σ) ¾0 для всех x R1 .

36 Глава 1. Основы теории вероятностей
Можно показать, что при любых a и σ>0 выполняется равенство
Z∞
f ( x, a, σ) dx = 1.
−∞
Тем самым функция f ( x, a, σ) удовлетворяет требованиям (2.1.1) и (2.1.2), предъявляемым по определению к функции плотности. У нормального распределения вероятностей есть и другие названия. Например, его часто называют гауссовским (по имени немецкого математика К. Ф. Гаусса1). Подробнее о нормальном распределении и о вероятностном смысле параметров a и σ будет рассказано ниже, в гл. 3. А сейчас обратим внимание на ряд важных особенностей функции плотности нормального распределения, которые хорошо видны и на графике.
1. Функция f ( x, a, σ) симметрична относительно точки a, т. е. f (a +x, a, σ) = f (a −x, a, σ) для любого x.
2. Функция f ( x, a, σ) достигает своего максимального значения
в точке a и этот максимум равен p 1 , т. е. значение плотности нор-
2πσ
мального распределения в точке a, тем больше, чем меньше значение параметра σ.
3. Как видно из графика плотности (рис. 1.17), вероятность отклониться от a больше чем на 2σ, не велика. Чтобы вычислить эту вероятность, необходимо сложить площади фигур под графиком плотности на интервалах (−∞, a −2σ) и (a +2σ, ∞). Напомним, что вся площадь под графиком плотности на всей числовой прямой равна 1. Таким образом, подобные отклонения от значения a — событие маловероятное. (Как видно на рис. 1.17, площади указанных фигур составляют малую часть от площади под кривой плотности на всей числовой прямой.) И обратно, вероятность попасть в область (a −2σ, a +2σ) довольно велика. Более точные значения этих вероятностей приведены в § 4 гл. 3.
3. Произвольная двумерная плотность распределения.
Пусть теперь Ω— это числовая плоскость R2 . Такое пространство элементарных исходов возникает всякий раз, когда в случайном эксперименте мы измеряем одновременно два признака, две характеристики явления, причем эти признаки могут изменяться непрерывно.
1 Карл Фридрих Гаусс (1777—1855) — великий немецкий математик, оказавший большое влияние на развитие различных областей математики: алгебры, теории вероятностей и математической статистики, теории чисел, дифференциальной геометрии. Активно работал в различных областях приложения математики: физике, астрономии, геодезии.
§ 2. Вероятности случайных событий |
37 |
|
|
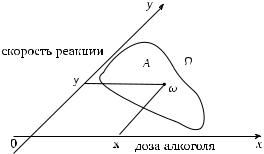
Рис. 1.18. Пространство элементарных исходов измерения дозы алкоголя и скорости реакции человека
Например, у человека мы можем измерять какие-либо две характеристики его фигуры, скажем рост и длину руки. В качестве двух других непрерывных характеристик человека можно рассмотреть дозу выпитого алкоголя и скорость реакции или дозу лекарства и артериальное давление. (Последние примеры представляют большой интерес для психологов и медиков.) Элементарными исходами во всех подобных случаях является пара чисел. Примем для них обозначение ( x, y), где x, y — числовые переменные. Пара ( x, y) играет роль элементарного события ω, числовая плоскость R2 или ее часть — это Ω, события A, B, C, … — это области на плоскости R2. На рис. 1.18 изображено пространство элементарных исходов для одного из упомянутых примеров.
Плотность вероятности здесь — это функция f ( x, y) двух числовых переменных, удовлетворяющая условиям
|
f ( x, y) ¾0 |
для всех x, y R2 |
|
(2.1.7) |
|
и |
ZZ∞ f ( x, y) dx dy = 1. |
|
|
|
|
|
|
|
(2.1.8) |
||
∞ |
−∞ |
|
|
|
|
|
|
плоскости R2.) |
|||
(Символ |
|
|
|||
−RR∞ |
обозначает интегрирование по всей |
|
2 |
|
|
Если известно, что Ω— это некоторая область в R |
|
, то полагают |
|||
|
f ( x, y) = 0 |
для ( x, y) / Ω. |
|
|
(2.1.9) |
38 |
Глава 1. Основы теории вероятностей |
|
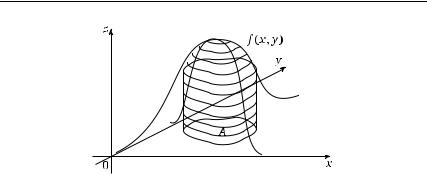
Рис. 1.19. Задание вероятности события A с помощью объема |
Вероятность P( A) события A, A Ω, есть
ZZ
P( A) = |
f ( x, y) dx dy. |
(2.1.10) |
A
С геометрической точки зрения величина (2.1.10) — это объем, заключенный между поверхностью, заданной уравнением z = f ( x, y), и областью A на координатной плоскости ( x, y), как это показано на рис. 1.19. Условие (2.1.8) означает, что объем, заключенный между упомянутыми поверхностью и координатной плоскостью, равен 1. Свойства (2.1.7), (2.1.8) обеспечивают для P( A) выполнение условий (2.0.1) и (2.0.2).
4. Двумерная нормальная плотность распределения.
Для приложений наиболее важна двумерная нормальная плотность. Ее можно рассматривать как обобщение уже упомянутой выше одномерной нормальной плотности. Двумерные нормальные плотности образуют целое семейство плотностей, зависящих от 5 параметров. Подробнее об этом см. в п. 5.4 гл. 3.
В простейшем случае двумерная нормальная плотность (часто называемая стандартной) имеет вид
f ( x, y) = |
1 |
e−x2 +2 y2 . |
(2.1.11) |
|
2π |
||||
|
|
|
Очевидно, что f ( x, y) >0 для любой пары чисел ( x, y) координатной плоскости. Можно показать (переходя к полярным координатам), что
ZZ∞
f ( x, y) dx dy = 1.
−∞
Тем самым, f ( x, y) из формулы (2.1.11) является функцией плотности.

|
§ 2. Вероятности случайных событий |
39 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.20. Стандартная двумерная нормальная плотность
График стандартной двумерной нормальной плотности представлен на рис. 1.20.
Формально функция f ( x, y) определена на всей числовой плоскости. Однако как видно из ее графика, ее значения существенно отличаются от нуля лишь в круге радиуса 3 с центром в нуле. Вероятность попасть в этот круг (т. е. объем под поверхностью плотности над этим кругом) превышает 0,99, т. е. это событие почти достоверное. Отсюда следует, что вероятность попадания в любую другую область, не пересекающуюся с указанным кругом, мала.
О понятии плотности вероятности. Понятие плотности не относится исключительно к вероятности. Плотность — это общенаучное понятие; оно относится к многим величинам, распределенным в пространстве (или времени) непрерывно — в отличие от тех, что сосредоточены в отдельных точках пространства (или моментах времени). Вспомним плотность вещества (массы), энергии, электричества и т. д. География оперирует таким понятием, как плотность населения, а в физике атмосферы важную роль играет плотность атмосферы.
Мы уже отмечали содержательный смысл плотности вероятности на числовой прямой, говоря, что вероятность попадания в малую окрестность точки a на числовой прямой примерно прямо пропорциональна величине плотности вероятности f (a) в этой точке:
P( A) ≈ f (a) ,
где — размер (длина) малого интервала, содержащего точку a.
С очевидными изменениями это правило вычисления вероятностей действует и в многомерном варианте. Пусть теперь A — область малого (стремящегося к нулю) диаметра, для которой a является внутренней точкой. Обозначим объем области A через |A|.
40 |
Глава 1. Основы теории вероятностей |
|
|
(В двумерном случае |A|— это площадь области A; в трехмерном — собственно объем, в случае большего числа измерений |A|— это объем области A соответствующего числа измерений.) Тогда
P( A) ≈ f (a)|A|,
или, более формально,
P( A) = f (a)|A|+o(|A|),
где o(|A|) (читается «о-малое» от объема области A) мало по сравнению с |A|.
Следовательно, f (a) и есть тот множитель, которым надо снабдить объем малой области, чтобы получить (приближенное) значение ее вероятности.
Упражнения
Могут ли приведенные ниже функции f ( x) выступать в качестве плотности распределения вероятностей в R1 ?
1. Функция f ( x), определенная как
0, если x < 0;
f ( x) = 1, если 0 ¶ x ¶1; 0, если x > 1.
2. Функция f ( x), определенная как
0, если x < 0;
f ( x) = 1, если 0 ¶ x ¶2; 0, если x > 2.
3. Функция f ( x), определенная как
0, если x < 0;
f ( x) = 2x, если 0 ¶ x ¶1; 0, если x > 1.
4. Функция f ( x), определенная как
|
|
0, |
|
|
если x < 0; |
f ( x) = |
6x(1 |
− |
x), |
если 0 ¶ x ¶1; |
|
|
|
|
|
|
|
|
0, |
|
если x > 1. |
||
