
tjurin_teorija_verojatn_978-5-94057-540-5_1
.pdf§ 3. Показательное распределение |
161 |
|
|
независимость развития яиц, покажите, что число взрослых потомков этого насекомого — случайная величина, распределенная по Пуассону с параметром λp.
§3. Показательное распределение
3.1.Определение и основные свойства
Плотность этого распределения — показательная функция. Показательная функция входит и в его функцию распределения, и в функцию надежности (определение см. ниже). Отсюда и название. Случайные величины с показательным распределением (они же — распределенные по показательному закону, они же — распределенные экспоненциально) в приложениях возникают как время безотказной работы (машины, прибора, изделия), как продолжительность жизни, длительность обслуживания, как время ожидания какого-либо случайного события и т. д. По смыслу этих перечислений ясно, что такие случайные величины принимают только положительные значения.
Определение 3.1.1. Распределение вероятностей на числовой прямой называют показательным (синоним — экспоненциальным), если
его плотность для каждого x R1 выражается формулой
|
|
1 e− |
x |
для x ¾0; |
|
|
θ |
|
|||
f ( x) = |
θ |
|
для x < 0, |
(3.1.1) |
|
0 |
|
||||
|
|
|
|
|
|
где θ >0 — произвольное число (параметр).
Формула (3.1.1) показывает, что вероятность распределена на положительной полуоси. Поэтому случайная величина, имеющая такую плотность, принимает только положительные значения.
Графический вид плотности показательного распределения с параметром θ приведен на рис. 1.16 п. 2.1 гл. 1.
Легко видеть, что формула (3.1.1) действительно задает плотность вероятностей, так как f ( x) ¾0 и
Z+∞
f ( x) dx = 1.
−∞
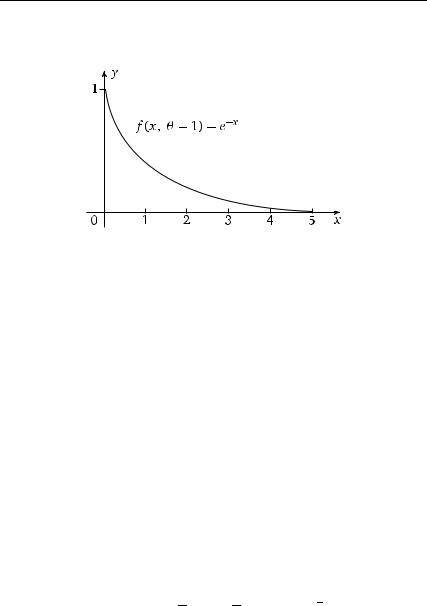
Показательное распределение с параметром θ =1 называют стандартным, а случайную величину с таким распределением — стандартной показательной случайной величиной. Плотность вероятно-
162 Глава 3. Некоторые важные распределения вероятностей
сти стандартной показательной случайной величины приведена на рис. 3.20. Заметим, что функция e−x довольно быстро убывает.
Рис. 3.20. Плотность стандартного показательного распределения
Связь стандартного и общего показательных распределений проста. Пусть Z обозначает стандартную показательную случайную величину. Для произвольного θ >0 введем новую случайную величину X, положив
X = θZ. |
(3.1.2) |
Теорема. Плотность случайной величины X =θZ (3.1.2) выражается формулой (3.1.1).
Доказательство. Ясно, что величина X, как и Z, с вероятностью 1 положительна. Поэтому достаточно найти плотность величины X только для положительной полуоси (на отрицательной полуоси плотность равна 0). По определению плотности для произвольных x >0, h >0 имеем
P( x < X < x +h) = f ( x)h +o(h). |
(3.1.3) |
Заменим X его выражением θZ (3.1.2), преобразуем форму обсуждаемого события и еще раз применим определение плотности, теперь уже плотности величины Z:
P( x < X < x +h) = P( x < θZ < x +h) = |
+o θh . (3.1.4) |
= P θx < Z < θx + θh = θh e−θx |
Сопоставив соотношения (3.1.3) и (3.1.4), получим, что плотность величины X из формулы (3.1.2) выражается формулой (3.1.1), что и требовалось.
§ 3. Показательное распределение |
163 |
|
|
Функция распределения F( x) = P( X ¶ x) показательного закона
с плотностью (3.1.1) равна |
|
|
|
|
|
|
F( x) = ¨ |
1 |
−e |
− |
x |
для x ¾0; |
|
θ |
(3.1.5) |
|||||
0 |
|
|
для x < 0. |
Для показательного распределения полезна и другая интегральная характеристика распределения
G( x) = P( X ¾ x).
Мы будем называть G( x) функцией надежности. Это название идет из техники. Когда X обозначает случайный момент поломки машины (время отсчитывается от момента ее запуска), величина G( x) для всякого x >0 обозначает вероятность того, что машина без поломок проработает не меньше времени x. В демографии G( x) называют функцией дожития (функцией выживания).
Функция G( x) при изменении x монотонно убывает (точнее, не возрастает) от 1 до 0. Для показательного распределения
G( x) = e− |
x |
для x ¾0. |
(3.1.6) |
θ |
Упражнения
1.Для случайной величины Z, имеющей стандартное показательное распределение, найдите вероятности следующих событий: а) P(Z ¶1); б) P(1 ¶Z ¶2); в) P(2 ¶Z ¶3); г) P(Z ¾3); д) P(Z ¾4).
2.Для случайной величины X, имеющей показательное распределение с параметром θ, найдите вероятности следующих событий: а) P(Z ¶θ); б) P(θ ¶Z ¶2θ); в) P(2θ ¶Z ¶3θ); г) P(Z ¾4θ); д) P(Z ¾5θ).
3.Время безотказной работы мобильного телефона фирмы «Шал- тай-Болтай» имеет показательное распределение с параметром θ =
=2 года. (Как будет показано ниже, параметр θ для показательного распределения означает среднее время безотказной работы.)
а) Какова вероятность того, что телефон выйдет из строя в первые полгода эксплуатации?
б) Какова вероятность того, что телефон безотказно прослужит 4 года?
4.В магазин с одним продавцом одновременно зашли два покупателя. Считая, что время обслуживания одного покупателя имеет показательное распределение с параметром θ =5 минут, найдите вероятность того, что второму покупателю придется ждать более 15 минут.

164 Глава 3. Некоторые важные распределения вероятностей
Математическое ожидание и дисперсия. Для их вычисления полезно вспомнить о связи (3.1.2) произвольного показательного распределения со стандартным. В силу соотношения (3.1.2) имеем
EX = θEZ, DX = θ2 DZ.
Поэтому достаточно вычислить эти моменты для стандартного показательного распределения. Их вычисляют, интегрируя «по частям». Например,
Z∞ Z∞ Z∞
EZ = xe−x dx = − x d(e−x) = −xe−x|∞0 + e−x dx = 1.
0 |
0 |
0 |
Отсюда следует, что |
|
|
|
EX = θ. |
(3.1.7) |
Так проясняется вероятностный смысл параметра θ показательного распределения: если X — это время безотказной работы (случайная величина), то θ — это ее математическое ожидание, т. е. средний срок службы изделия. Если X — время обслуживания, то θ — среднее время обслуживания.
Аналогичными вычислениями находим и дисперсию величины X: сначала находим, что EZ2 =2, откуда следует, что DZ =EZ2 −(EZ)2 =1, а затем получаем, что
DX = θ2 .
Отсюда следует, что стандартное отклонение (т. е. квадратный корень из дисперсии) случайной величины, имеющей показательное распределение с параметром θ, равно θ.
Замечание. Иногда функцию плотности показательного распределения задают в виде
f ( x) = ¨ |
ae−ax |
для x ¾0; |
0 |
для x < 0, |
где a >0 — произвольный параметр. Сравнивая это выражение с формулой (3.1.1), получаем a = θ1 . В некоторых случаях эта параметриза-
ция может быть удобной, но a не имеет такого ясного вероятностного истолкования, как параметр θ для соотношения (3.1.1).
Упражнения
1. Для случайной величины Z, имеющей стандартное показательное распределение, найдите EZ3.

§ 3. Показательное распределение |
165 |
|
|
2. Время безотказной работы некоторого изделия имеет показательное распределение со средним временем безотказной работы 3 года. Какова вероятность того, что изделие безотказно проработает 3 года? (Сравните полученный ответ с 1/2.) Справедливо ли утверждение, что половина изделий безотказно служит меньше среднего срока безотказной службы, а половина — больше среднего срока службы?
Две вероятностные модели, приводящие к показательным распределениям. Распространенность показательного распределения при описании случайного времени службы и обслуживания подтверждается не только наблюдениями, но и имеет формальное математическое обоснование. Ниже мы приведем две математические модели, приводящие к показательному распределению. Одновременно это даст нам представление о тех предпосылках, в которых возникает это распределение. Можно сказать, что показательное распределение является простейшей моделью для описания явлений типа «времени службы». Наряду с этим распределением для описания подобных задач предложены и значительно более сложные распределения, учитывающие специфические особенности рассматриваемых явлений.
Время ожидания случайного события. Предположим, что некоторое случайное событие может произойти в любой момент времени
ичто связанные с этим вероятности имеют следующие свойства.
1.Вероятность того, что за время [t, t +h], где t >0, h >0, произойдет одно событие, равна ah +o(h) — вне зависимости от того, когда произошло предыдущее событие; здесь a > 0 — некоторое число, не зависящее от t.
2.Вероятность того, что за время [t, t + h] произойдут два или больше случайных событий, есть o(h).
Из предположений 1 и 2 следует, что вероятность того, что за время (t, t +h) событий нет, равна 1 −ah −o(h).
Начнем отсчет времени ожидания случайного события с момента t =0. Обозначим момент осуществления случайного события через X. Ясно, что X — случайная величина, X ¾0. Вычислим функцию надежности случайной величины X, т. е.
G(t) = P( X ¾ t)
для произвольного t > 0. Событие ( X ¾t) означает, что в течение времени (0, t) не произошло ни одного события. Вероятность именно этого события и надо подсчитать.
Разделим отрезок времени (0, t) на n равных частей точками 0, t , t t n
2 n , …, (n −1) n, t. Исход «за время (0, t) событий не было» означает,

166 Глава 3. Некоторые важные распределения вероятностей
что событий не было ни на одном из интервалов. То есть исход «за время (0, t) событий не было» можно записать как пересечение следующих событий:
( X ¾ t) = \n (за время hk −n 1 t, nk tiсобытий не было).
k=1
Перечисленные в этой формуле n случайных исходов независимы,
и вероятность каждого из них равна 1 −a nt −o 1n . Поэтому
P( X ¾ t) = Yk=1 1 − atn −o |
1n |
= h1 − atn −o n1 i. |
n |
|
n |
|
|
Переходя к пределу по n →∞, получаем, что для произвольного t >0 справедливо равенство
P( X ¾ t) = e−at. |
(3.1.8) |
Мы видим, что это показательная функция надежности. Следовательно, если вероятностные свойства случайных событий такие, как в п. 1 и 2, то случайное время ожидания этого события распределено по показательному закону.
Случайное время службы. Обозначим через X время службы некоторого изделия от начала его работы до первой поломки (инженеры говорят — отказа). Мы знаем, что это время X случайное. Предположим, что в процессе работы данное изделие не становится хуже, т. е. не изнашивается, не стареет. Математически это можно выразить так: для изделия, прослужившего некоторое время s >0, последующее случайное время службы имеет такое же распределение, как и время службы для нового изделия. Коротко, с помощью условной вероятности это можно записать так: для любых s >0, t >0 справедливо равенство
P( X ¾ s +t | X ¾ s) = P( X ¾ t) |
(3.1.9) |
Условную вероятность в левой части равенства (3.1.9) преобразуем по ее определению в выражение вида
P( X ¾ s +t | X ¾ s) |
= |
P( X ¾ s +t) |
, |
|
P( X ¾ s) |
P( X ¾ s) |
|||
|
|
так как событие ( X ¾s) есть следствие события ( X ¾s +t) для s >0, t >0. Отсюда и из формулы (3.1.9) получаем соотношение
P( X ¾ s +t) = P( X ¾ s)P( X ¾ t),

§ 3. Показательное распределение |
167 |
|
|
или, через функцию надежности G( x) =P( X ¾x), |
|
G(s +t) = G(s)G(t) для s, t ¾0. |
(3.1.10) |
Решая это уравнение, надо учесть два условия:
1)функция G(t) как функция надежности должна быть убывающей (точнее, невозрастающей),
2)G(0) =1.
При этих условиях решение уравнения (3.1.10) имеет вид
G(t) = e−at для t ¾0, |
(3.1.11) |
где a >0 — произвольная постоянная (без доказательства).
Мы видим, что найденная функция — это известная нам функция надежности показательного распределения. Итак, распределение случайной величины X, обладающей свойством (3.1.9), показательное. Это характеристическое свойство показательного распределения часто называют «отсутствием памяти» у показательно распределенных случайных величин.
Если мы немного упростим задачу и дополнительно предположим, что функция G(t) дифференцируема, то и сами сможем вывести формулу (3.1.11). Дифференцируемость функции надежности G(t) означает, что у распределения вероятностей есть плотность. Поэтому предположение о дифференцируемости означает, что мы имеем распределение, которое не только обладает свойством (3.1.9), но и имеет плотность.
Продифференцируем уравнение (3.1.10) по какой-либо из переменных s или t; для определенности — по переменной t. Получим, что
G′(s +t) = G′(t)G(s).
Разделив это соотношение на (3.1.10), получим уравнение
G′(s +t) |
= |
G′(t) |
для всех s, t ¾0. |
G(s +t) |
|
G(t) |
|
Из этого следует, что при всех t ¾0 выполняется равенство
G′(t)
G(t) = const.
Заметим, что
G′(t) = d ln G(t).
G(t) dt
Функция, производная которой постоянна, — это линейная функция. Следовательно,
ln G(t) = bt +c,

168 Глава 3. Некоторые важные распределения вероятностей
где b и c — произвольные числа. Отсюда следует, что
G(t) = ecebt.
С учетом того, что G(0) =1 и что G(t) — монотонно убывающая функция, получим соотношение (3.1.11).
Функция риска. В этом пункте откажемся от предположения, что случайное время безотказной работы X имеет показательное распределение. Примем более общую точку зрения: X — это непрерывная случайная величина, которая может принимать только положительные значения. Плотность распределения вероятностей этой случайной величины, как обычно, обозначим через f ( x). Рассмотрим вероятность того, что, исправно прослужив время x >0, изделие при этом условии откажет в интервале ( x, x +h), h >0. Эта вероятность равна
P( x < X < x +h | X > x) = |
P(x < X < x +h) |
. |
P( X > x) |
Вероятность P( x < X <x +h) при малых h можно записать через плотность вероятности f ( x):
P( x < X < x +h) = f ( x)h +o(h),
а P( X > x) есть не что иное, как функция надежности G(x). Отсюда для h →0 получаем
|
|
|
f (x) |
|
|
P( x < X < x +h | X > x) = |
|
h +o(h). |
|
||
G(x) |
|
||||
Величина |
|
||||
r( x) = |
f (x) |
(3.1.12) |
|||
|
|
||||
G(x) |
|||||
как функция от x ¾0 называется функцией риска.
Функция риска — удобный объект для обсуждения статистических свойств случайного времени службы изделия, безотказной работы, времени жизни, времени ожидания, времени обслуживания и т. д. В технике функцию риска называют функцией интенсивности отказов; в демографии — это сила смертности и т. д.
Для показательного распределения (3.1.1) функция риска не зависит от x >0. Она постоянна и равна θ1 . В реальности функция риска
обычно возрастает, что и означает старение (износ) всякого изделия в процессе его работы. Это старение (уменьшение надежности) может быть на определенных отрезках времени медленным и незаметным. Именно для таких периодов для описания времени службы применяют показательное распределение. Для описания функции риска
§ 3. Показательное распределение |
169 |
|
|
на более длительных промежутках используют более сложные формулы. В демографии, например, употребительна формула Мейкема— Гомперца: для x ¾0 получают
r( x) = α+βeγx |
(3.1.13) |
где α>0, β >0, γ>0 — некоторые постоянные. Их численные значения приблизительно находят по наблюдениям. Как частный случай формула (3.1.13) содержит и показательное распределение: оно получается при β =0.
3.2.Компьютерный практикум
Вэтом пункте мы покажем, как моделировать случайную величину X, распределенную по показательному закону, и научимся вычислять на компьютере в пакете EXCEL вероятности событий вида
P( X ¶x) и P( X >x).
3.2.1. Моделирование случайных величин, распределенных по показательному (экспоненциальному) закону распределения. К сожалению, экспоненциальное распределение не входит в группу распределений, для которых в EXCEL можно непосредственно вызвать процедуру генерации случайных чисел, как это было сделано для биномиального и пуассоновского распределений. Однако можно применить общий универсальный метод моделирования непрерывной случайной величины с распределением, имеющим монотонную функцию распределения F( x). Он состоит в следующем. Пусть X — случайная величина, имеющая равномерный закон распределения на [0, 1]. Напомним, что плотность такого закона распределения равна 1 на [0, 1] и 0 вне [0, 1]. Равномерное распределение входит в группу распределений, которые можно смоделировать непосредственно в EXCEL вызовом процедуры Генерация случайных чисел. Пусть X — случайная величина, имеющая равномерный на [0, 1] закон распределения. Тогда новая случайная величина Y = F−1 ( X), полученная подстановкой X в функцию, обратную функции распределения F( x), имеет нужный закон распределения с функцией распределения F( x). В самом деле, P(Y ¶x) = P(F−1( X) ¶x) = P( X ¶F( x)) = F( x), так как функция распределения равномерного на [0, 1] закона линейна на этом отрезке. Применим этот метод для моделирования экспоненциального распределения с параметром θ. Плотность этого закона распределения была определена в гл. 3 формулой (3.1.1). Очень часто функцию плотности экспоненциального закона распределения
170 Глава 3. Некоторые важные распределения вероятностей
параметризуют по-другому, с помощью параметра λ= |
1 |
: |
|||
f ( x, λ) = ¨ |
|
|
|
θ |
|
λ |
−λx |
для x ¾0; |
|
|
|
0 e |
|
для x < 0. |
|
|
|
Именно такая параметризация и обозначение соответствующего параметра символом λ приняты в пакете EXCEL. Соответствующая этой плотности функция распределения имеет вид F( x) = 1 − − exp(−λx). Тогда из равенства F(Y ) = X, т. е. 1 − exp(−λY ) = X,
выразим Y через X. Легко получить, что Y =−ln(1λ−X ) . Это значение
Y и будет смоделированным значением, имеющим заданное экспоненциальное распределение, если X имеет равномерный на [0, 1] закон распределения.
Моделирование в EXCEL случайных величин, имеющих экспоненциальное распределение, рассмотрим на следующем ниже примере.
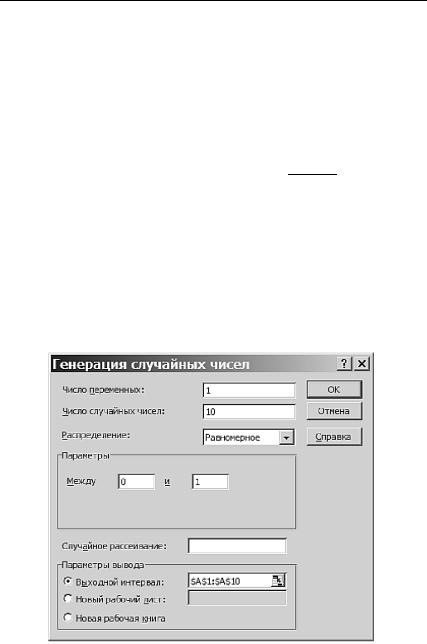
Пример 3.3.1. Пусть среднее время безотказной работы холодильника составляет 10 лет. Это означает, что параметр экспоненциального закона θ =10. Введем величину λ=1/θ, которая в примере равна λ=1/θ =0,1. Смоделируем последовательность длины 10 с этим зако-
Рис. 3.21. Генерация 10 равномерно распределенных на [0, 1] чисел
