
tjurin_teorija_verojatn_978-5-94057-540-5_1
.pdf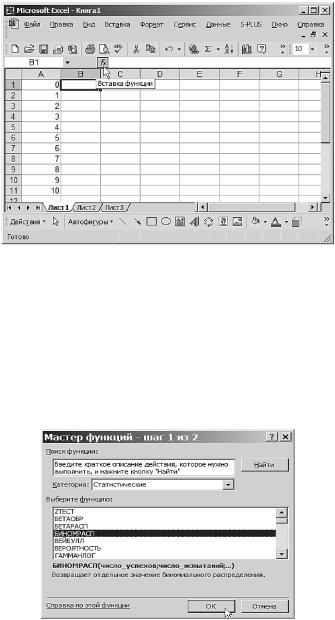
§ 1. Биномиальное распределение |
141 |
|
|
Рис. 3.6. Вставка функции
курсор в первую строку второго столбца и мышкой перейдем на поле fx , соответствующее вставке функции (см. рис. 3.6).
Кликнув левой клавишей мыши на поле fx , откроем диалоговое окно Мастер функций шаг 1 из 2. В поле Категория: выберем значение Статистические. После этого в поле Выберите функцию: отобразятся функции, объединенные в эту категорию функций. В этом поле выберем функцию БИНОМРАСП (см. рис. 3.7).
Рис. 3.7. Выбор функции для вычисления вероятностей биномиального распределения

142 Глава 3. Некоторые важные распределения вероятностей
Рис. 3.8. Ввод параметров биномиального распределения
Нажав на клавишу OK , вызовем новое окно Аргументы функции для ввода аргументов этой функции. В поле Число_успехов введем
A1. В поле Число_испытаний введем 10. В поле Вероятность_успеха
введем 0,5. В поле Интегральная введем 0 или ЛОЖЬ. (В этом поле вводится значение аргумента соответствующей функции, которое может принимать логические значения ЛОЖЬ (0) или ИСТИНА (1). При задании 0 будут вычисляться вероятности биномиального закона распределения P( X = k), k =0, 1, 2, …, n, а при задании 1 — значения функции распределения P( X ¶k).) Заполнение окна Аргументы функции для нашего примера изображено на рис. 3.8.
После нажатия на клавишу OK в ячейке B1 электронной таблицы отобразится значение вероятности того, что биномиальная случайная величина примет значение, заданное в ячейке A1. Распространим эту формулу на столбец B, протащив маркер заполнения вниз до ячейки B11 при нажатой левой клавиши мыши (тем самым скопировав формулу на соответствующие ячейки столбца B). Таким образом, переменная столбца B примет значения биномиальных вероятностей, соответствующих параметрам этого распределения n =10 и p =0,5. Результат вычисления показан на рис. 3.9.
Теперь можно изобразить график зависимости вероятностей P( X = =k), записанных во втором столбце, от числа успехов k, записанных в первом столбце. Этот график, построенный с использованием стандартных средств EXCEL, изображен на рис. 3.10.

§ 1. Биномиальное распределение |
143 |
|
|
Рис. 3.9. Распространение формулы на все значения столбца B
Рис. 3.10. График вероятностей биномиального распределения при p =0,5, n =10

144 Глава 3. Некоторые важные распределения вероятностей
Рис. 3.11. График вероятностей биномиального распределения при p =0,25, n =10
Рис. 3.12. График вероятностей биномиального распределения при p =0,9, n =10

§ 1. Биномиальное распределение |
145 |
|
|
Посмотрите на этот график. Распределение вероятностей симметрично относительно центрального значения k =5, т. е. P( X =k) = =P( X =n −k).
Упражнение. Вычислите вероятности биномиального закона распределения и постройте подобным же образом графики зависимости вероятностей биномиального закона от числа успехов для n =10 при других значениях вероятности успеха в одном испытании: p = 0,25
и p =0,9.
Получилось? Будут ли распределения симметричны? Сравните ваши результаты с результатами, изображенными на рис. 3.11 и рис. 3.12.
1.2.4. Вычисление биномиальных вероятностей вида P( X ¶k). С помощью этой же самой функции БИНОМРАСП можно вычислять вероятности событий ( X ¶k) для числа успехов X в n испытаниях Бернулли. Для этого четвертый аргумент этой функции должен быть равен 1 (ИСТИНА), что означает, что вычисляется функция распределения (интегральная функция). Вычисление вероятностей событий ( X ¾k),
(k1 |
¶X ¶k2) сводится к вычислению предыдущих вероятностей. |
|||||
|
|
|
X |
|
|
|
|
Пример 3.1.3. Вычислим P |
|
n |
− p |
¾ǫ |
, т. е. вероятность того, |
|
|
|
|
|
|
|
что частота успехов в n испытаниях Бернулли отклоняется от истинной вероятности успеха в одном испытании не менее чем на ǫ. Пусть n = 100, p = 0,2, ǫ =0,05. Запишем эту вероятность таким образом, чтобы можно было воспользоваться функцией БИНОМРАСП:
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
X |
−0,2 ¾0,05 |
=1−P |
|
X |
−0,2 <0,05 =1−P(15 < X <25) = |
||||
|
100 |
100 |
||||||||||
|
|
|
|
− |
|
− |
|
|
|
|
− |
|
|
|
= 1 |
|
P( X ¶24) |
|
P( X ¶15) |
= 1 |
P( X ¶24)+P( X ¶15). (1.2.1) |
||||
Поставим курсор в ячейку электронной |
таблицы, в которой будет на- |
|||||||||||
ходиться результат вычислений. Затем в поле fx введем следующее
Рис. 3.13. Результат вычисления P |
|
X |
−0,2 |
¾0,05 |
|
||||
100 |
||||
|
|
|
|
|

146 Глава 3. Некоторые важные распределения вероятностей
выражение (формулу):
= 1 −БИНОМРАСП(24; 100; 0,2; 1) +БИНОМРАСП(15; 100; 0,2; 1).
Результат вычислений изображен на рис. 3.13. Вычисленная вероятность с точностью до округления равна 0,26.
|
|
|
|
Упражнения |
|
|
|
|
|
|
|||
1. Вычислите |
|
X |
|
¾ |
|
|
= |
|
= |
|
=0,05. Срав- |
||
P n −p |
ǫ , если n |
100, p |
|
||||||||||
|
|
|
=0,5, ǫ |
|
= |
|
|||||||
ните вычисленную вероятность |
при разных p (p |
|
0,2 и p |
|
0,5). |
||||||||
2. Что будет, если |
число |
испытаний n увеличить в два |
раза? Срав- |
||||||||||
ните соответствующие вероятности.
1.3.Задачи
1.Задача о дегустаторе. В некоторых областях деятельности требуются люди с повышенной чувствительностью к определенным раздражителям. Их обычно именуют дегустаторами. При приеме на работу дегустатора можно использовать следующий простой тест для выявления дегустаторских способностей. Тестируемому предлагают три одинаковых по виду образца, один из которых отличается по своим свойствам (скажем, вкусу или запаху) от двух других. Задача тестируемого — правильно указать отличающийся образец. Подобный опыт повторяют 10 раз.
1.1.Вычислите вероятность того, что тестируемый, не обладая свойствами дегустатора, даст: более 9 правильных ответов; более 8 правильных ответов.
1.2.Найдите математическое ожидание и дисперсию числа правильных ответов человека, не обладающего способностями дегустатора.
1.3.Предположим, что вероятность правильного ответа дегустатора в одном эксперименте с предъявлением трех образцов равна 0,9.
Всерии из 10 испытаний найдите вероятность получить от дегустатора: более 8 правильных ответов, более 9 правильных ответов.
2.Задача о выборочном контроле. Вероятность p встретить бракованное изделие при выборочном контроле качества при нормальном процессе производства равна 0,002.
2.1.Найдите вероятность того, что в партии из 500 изделий: а) не будет ни одного бракованного изделия; б) будет не более 1 одного бракованного изделия. Каким из приближений следует воспользоваться при вычислении этих вероятностей?
§ 1. Биномиальное распределение |
147 |
|
|
2.2.Найдите вероятность того, что в партии из 500 изделий встретится более 3 бракованных изделий. Можно ли при этом считать с вероятностью 0,95, что в процессе производства появились сбои?
3. Задача о маркетинговом исследовании. В выборочном опросе
100 потребителей целевой группы некоторого продукта до проведения рекламной кампании выяснилось, что 40 из них предпочитают покупать продукт данного производителя.
3.1.Укажите, в каких пределах с вероятностью 0,95 может варьироваться число потребителей Sn, предпочитающих данный продукт,
ваналогичном выборочном опросе каких-то других n =100 потребителей из этой целевой группы. Другими словами, найдите такое целое
x, что P(40 −x ¶Sn ¶40 + x) ≈0,95. Каким из приближений следует воспользоваться при вычислении этой вероятности?
3.2.После проведения рекламной кампании выборочный опрос 100 потребителей целевой группы показал, что продукт данного производителя предпочитают покупать 48 человек. Можно ли считать, что рекламная кампания способствовала росту числа потребителей продукта данного производителя?
3.3.После проведения рекламной кампании выборочный опрос 100 потребителей целевой группы показал, что продукт данного производителя предпочитают покупать только 35 человек. Можно ли считать с вероятность 0,95, что в результате рекламной кампании сократилось число потребителей продукта данного производителя, т. е. реклама подействовала негативно?
4. Случайная величина X имеет биномиальное распределение с параметрами p =0,5 и n =20. Найдите наименьшее такое значение
k, что
P(|X −np| > k) < 0,005.
5.Серию испытаний Бернулли, вероятности успеха и неудачи в которых обозначим соответственно p и q, проводят до появления первого успеха. Длина серии (число испытаний), таким образом, оказывается случайной величиной. Найдите для этой случайной величины распределение и математическое ожидание.
6.Одновременно проводят m (m — натуральное число) независи-
мых испытаний Бернулли, в которых ( pi, qi) суть вероятности успехов и неудач, i =1, …, m. Серия испытаний заканчивается, как только
водном из испытаний произойдет успех. Длина серии, таким образом, оказывается случайной величиной. Для этой случайной величины найдите распределение и математическое ожидание.
7.В вашем распоряжении несимметричная монета. Как с помощью бросаний этой монеты (бросания предполагаются независимы-

148 Глава 3. Некоторые важные распределения вероятностей
ми) получить испытания Бернулли, в которых вероятность успеха равна 0,5?
§2. Распределение Пуассона
2.1.Определение и основные свойства
Распределение Пуассона играет важную роль в теории массового обслуживания (см. [9, 10]), страховании (см. [28, 29]), теории надежности (см. [7]), теории связи, ряде вопросов физики и т. д. — словом, всюду, где в течение определенного времени может происходить случайное число каких-то событий (заявок на обслуживание, страховых случаев, отказов оборудования, телефонных вызовов, радиоактивных распадов, несчастных случаев и т. п.). Распределению Пуассона часто следуют количества событий, если эти события происходят редко и случайно. (К обсуждению распространенности распределения Пуассона мы вернемся в § 4 гл. 4.) Заметим, что число событий может принимать лишь целые неотрицательные значения.
Определение 2.1.1. Распределением Пуассона называют распределение вероятностей между целыми неотрицательными числами, когда на долю числа m приходится вероятность
p(m, λ) = e−λ λm , где m = 0, 1, …; |
(2.1.1) |
m!
здесь λ>0 — параметр распределения.
Формула (2.1.1) действительно задает распределение вероятностей на множестве целых неотрицательных чисел, так как p(m, λ) >0 для
всякого m =0, 1, … и
X∞
p(m, λ) = 1.
m=0
Доказательство этого опирается на следующее математическое соотношение:
∞ |
m |
|
mX=0 |
|
|
λm! = eλ |
(2.1.2) |
для любого λ>0. Это соотношение часто бывает нужно при изучении распределения Пуассона. Понадобится оно и нам.
Определение 2.1.2. Случайная величина X называется распределенной по Пуассону с параметром λ>0, если X принимает целые неотрицательные значения m =0, 1, … и
P( X = m) = e−λ λm . |
(2.1.3) |
m! |
|

|
|
|
|
|
§ 2. Распределение Пуассона |
149 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.14. Вид распределения Пуассона для различных значений λ
Если о случайной величине X, имеющей распределение Пуассона, мы говорим как о числе случайных событий в течение некоторого фиксированного времени, то параметр λ (как будет показано ниже) имеет ясный смысл. Это среднее число случайных событий за это время. В таком случае понятно, что если мы меняем временной интервал, в котором фиксируем наступление событий, то пропорционально должно изменяться и среднее число событий. Например, если случайное число посетителей крупного магазина за четыре недели составляет в среднем 28000 человек, то за неделю его в среднем посещает 7000 человек, а за день — 1000 человек при условии однородности во времени потока посетителей. Последнее условие может и нарушаться, скажем, в выходные дни посетителей в среднем может быть больше, чем в будние.
На рис. 3.14 показаны значения вероятностей p(m, λ) для нескольких значений λ.
Область применения. Как было сказано выше, распределение Пуассона играет важную роль во многих прикладных областях. В теории массового обслуживания на этом распределении, в частности, базируются расчеты требуемых мощностей для обслуживания клиентов (более подробно см. [10]). В страховании оно используется для расчетов условий страховых договоров и страховых резервов кампаний (см. [29]). Обобщенно можно сказать, что потребность в распределе-

150 Глава 3. Некоторые важные распределения вероятностей
нии Пуассона возникает в тех случаях, когда вероятность случайного события p мала, но число таких событий n велико. Скажем, вероятность пожара в отдельной квартире в течение суток довольно мала, но число таких квартир в большом городе сотни тысяч или даже миллионы. Статистика показывает, что в больших городах ежедневно случаются десятки (и даже сотни) пожаров в зависимости от величины города. Если величина np постоянна, то распределение случайного числа пожаров за сутки хорошо согласуется с распределением Пуассона, причем параметр распределения Пуассона равен λ=np. Математически более подробно мы обсудим этот вопрос в § 4 гл. 4.
Упражнения
1. На заданном участке шоссе с интенсивным движением в дневное время в среднем происходит 1 авария за 2 часа. Считая, что число аварий имеет распределение Пуассона, найдите вероятность того, что
втечение 8 дневных часов на этом участке: а) не произойдет ни одной аварии; б) произойдет менее 2 аварий; в) произойдет более 3 аварий.
2.Рыбак за час в среднем вылавливает 6 рыб. Какова вероятность того, что в течение 10 минут он:
а) не выловит ни одной рыбы? б) выловит ровно одну рыбу? в) выловит более 2 рыб?
3.В магазин дорогой модной одежды в среднем заходят 6 человек
вчас. Считая, что число посетителей распределено по Пуассону, найдите вероятность того, что в течение десяти минут зайдут:
а) более одного человека; б) два человека; в) более двух человек.
Сколько продавцов, на ваш взгляд, целесообразно держать в магазине, если считать, что продавец тратит на обслуживание одного клиента в среднем те же десять минут? Дайте обоснованный ответ.
Математическое ожидание и дисперсия. Покажем, что для распределенной по Пуассону случайной величины X выполняются соотношения
EX = λ, DX = λ. |
(2.1.4) |
По определению математического ожидания EX в нашем случае
EX = X∞ mP( X = m) = X∞ me−λ λm . m!
m=0 |
m=0 |
