
tjurin_teorija_verojatn_978-5-94057-540-5_1
.pdf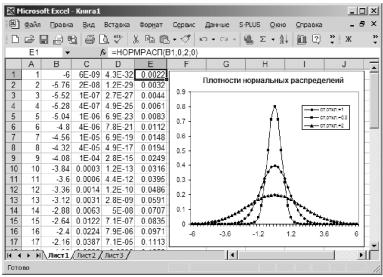
§ 4. Нормальное распределение |
191 |
|
|
Упражнение. Постройте графики функций плотности нормальных законов распределения с нулевым математическим ожиданием и стандартными отклонениями σ1 =2 и σ2 =0,5. Сравните их с графиками на рис. 3.36.
Рис. 3.36. Графики функций плотности нормальных распределений с различными стандартными отклонениями: σ1 =1; σ2 =0,5; σ3 =2
4.2.3. Вычисление функции, обратной к функции распределения стандартного нормального закона, — функции квантилей стандартного нормального распределения. Вычисление квантилей заданного уровня для произвольного нормального распределения. Для вычисления квантилей стандартного нормального распределения в EXCEL надо применить функцию НОРМСТОБР. Она имеет один аргумент — вероятность.
Пример 3.4.3. Вычислим квантили стандартного нормального распределения нескольких заданных уровней. В столбце A задано несколько уровней вероятностей p. Выбранные уровни используются в математической статистке в задачах проверки статистических гипотез. Вызовем функцию НОРМСТОБР и в качестве аргумента введем адрес ячейки, в которой находится соответствующий уровень вероятности. Заполнение окна показано на рис. 3.37.

192 Глава 3. Некоторые важные распределения вероятностей
Рис. 3.37. Заполнение полей для функции НОРМСТОБР
Результат вычисления, распространенный на весь столбец B, изображен на рис. 3.38.
Обратите внимание на то, что квантили стандартного нормального распределения уровней p и 1 − p симметричны относительно нуля. Квантиль уровня 0,5 (медиана), которая равна нулю, вычислена в EXCEL с точностью 5,5 ·10−10 .
Вычисление квантилей заданных уровней для произвольного нормального распределения проводится в EXCEL с помощью функции НОРМОБР, которая имеет 3 параметра — кроме вероятности нужно еще задать математическое ожидание (Среднее) и стандартное отклоне-
ние (Стандартное_откл).
Рис. 3.38. Вычисление квантилей стандартного нормального распределения

§ 4. Нормальное распределение |
193 |
|
|
Пример 3.4.4. Вычислим квантили уже рассмотренных уровней для упоминавшегося выше нормального распределения для роста девушек. Заполнение полей функции НОРМОБР показано на рис. 3.39.
Рис. 3.39. Заполнение полей для вызова функции НОРМОБР
Результаты вычислений приведены на рис. 3.40.
Рис. 3.40. Вычисление квантилей нормального распределения с параметрами a =168, σ=6
На рис. 3.40 видно, что нижняя квартиль примерно равна 164 см, а верхняя квартиль 172 см. Межквартильный размах при этом равен 172 −164 =8 см. В межквартильный интервал попадает 50% вероят-
194 Глава 3. Некоторые важные распределения вероятностей
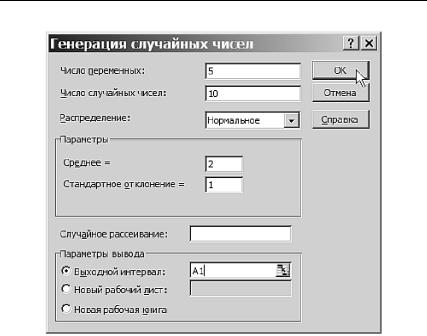
Рис. 3.41. Заполнение полей окна Генерация случайных чисел для моделирования нормально распределенных последовательностей случайных чисел
ности. В нашем примере квартили совпали с нижней и верхней границами роста женщин, считающегося средним. В рассмотренном выше примере мы уже обращали на это внимание.
4.2.4. Моделирование нормально распределенных случайных величин. Покажем, как в EXCEL моделировать случайные величины с нормальным распределением. Выберем уже хорошо знакомую нам процедуру Генерация случайных чисел (напомним, что она вызывается из меню Анализ данных, вызванного из главного меню Сервис). Смоделируем 5 нормальных выборок объема 10 каждая с математическим ожиданием a =2 и стандартным отклонением σ=1. Заполнение полей соответствующего окна изображено на рис. 3.41.
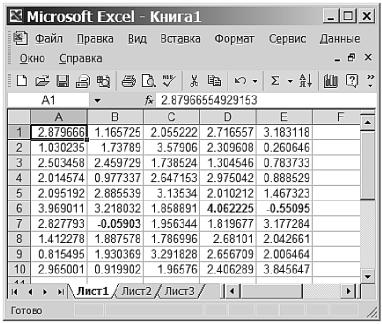
Результат моделирования показан на рис. 3.42.
Упражнение. Посмотрите на таблицу (рис. 3.42) и ответьте на следующие вопросы.
1.Найдите минимум и максимум из всех 50 чисел.
2.Сколько значений отклоняется от среднего на величину, большую чем 2σ?
§ 5. Многомерное нормальное распределение |
195 |
|
|
Рис. 3.42. Смоделированные нормально распределенные последовательности с параметрами a =2, σ=1
3. Подсчитайте, какая доля значений отклоняется от среднего менее чем на σ.
§5. Многомерное нормальное распределение
Вэтом параграфе мы будем обсуждать свойства и совместное поведение сразу нескольких случайных величин. До сих пор мы обсуждали отдельно взятые случайные величины. Несколько случайных величин, рассматриваемых вместе и измеряемых в одном случайном эксперименте, называют многомерной случайной величиной. Рассматривавшиеся до сих пор случайные величины, если надо подчеркнуть различие, называют одномерными случайными величинами. Многомерные случайные величины можно рассматривать как векторы со случайными компонентами (случайные векторы). Поэтому при обсуждении многомерных случайных величин мы будем использо-

196 Глава 3. Некоторые важные распределения вероятностей
вать средства линейной (векторной) алгебры — единственный раз
вкниге.
Счастным случаем многомерных случайных величин — двумерной случайной величиной, или, проще говоря, парой случайных величин мы уже сталкивались в § 3 гл. 2. Там были введены понятия совместного и частных (маргинальных) распределений подобных случайных величин, описаны основные числовые характеристики этих случайных величин и, в частности, рассказано о ковариации и корреляции. Материал настоящего параграфа обобщает эти понятия и характеристики для двумерной случайной величины на случай многомерной случайной величины.
На практике многомерные случайные величины (случайные векторы) возникают как наборы различных количественных характеристик какого-либо объекта, случайно выбранного из некоторой совокупности. Так, для случайно выбранного мужчины в качестве нескольких таких характеристик могут выступать рост, вес, объем груди и т. д. Для случайно выбранного предприятия — численность занятых на нем сотрудников и финансовые показатели. Для случайно выбранного региона РФ такими характеристиками могут служить показатели его социально-экономического развития.
Переход от изучения отдельной характеристики объекта к совместному изучению нескольких характеристик важен во многих естественных, технических и социально-экономических областях. Он позволяет строить математические модели взаимосвязи характеристик, осуществлять управление одними из них через другие, прогнозировать их значения в будущем. В ряде научных дисциплин подобные исследования давно уже оформились в самостоятельные направления. В экономических науках это эконометрика, в психологии — психометрия, в медико-биологических науках — биометрия и т. д.
Материал этого параграфа подразумевает, что читатели знакомы с основными элементами курса «линейной алгебры»: вектором, матрицей, произведением матрицы на вектор, транспонированными матрицами, определители матрицы и т. п.
При этом пункт 5.4, где рассказывается о двумерном нормальном распределении, более прост и нагляден.
5.1. Случайные векторы и матрицы
Определение 5.1.1. Случайная матрица X = kxijk есть матрица, элементы которой xij — это случайные величины, измеряемые в од-
§ 5. Многомерное нормальное распределение |
197 |
|
|
ном случайном эксперименте и, следовательно, имеющие совместное распределение вероятностей. Случайный вектор (столбец или строка) есть частный случай случайной матрицы.
Как и для двумерной случайной величины (см. п. 3.1 гл. 2), от совместного распределения вероятностей случайной матрицы или вектора можно перейти к частному (маргинальному) распределению отдельных его компонент, которые при этом рассматриваются как одномерные случайные величины. Это значит, что мы можем вычислять математическое ожидание, дисперсию и другие числовые характеристики отдельной случайной компоненты при условии существования этих характеристик.
Определение 5.1.2. Математическое ожидание случайной матрицы X =kxijkесть матрица, обозначаемая EX, элементы которой суть Exij, т. е. математические ожидания элементов матрицы X.
Теорема 5.1.1 (Без доказательства). Пусть X, Y — случайные матрицы, измеряемые в одном случайном эксперименте, A, B, C — постоянные (не случайные) матрицы. Тогда
E( X +Y ) = EX +EY , E( AXB +C) = A(EX)B +C,
если размерности матриц X, Y , A, B, C согласованы в том смысле, что указанные действия возможны, а также если EX, EY существуют.
В частности, если X — случайный вектор, A — постоянная (не случайная) матрица, b — постоянный вектор, то
E( AX +b) = AEX +b,
когда EX существует и указанные операции существуют. Приведенная теорема говорит, что переход от случайного векто-
ра (случайной матрицы) к математическому ожиданию — операция линейная. Это обобщает известное для случайных величин линейное свойство математического ожидания.
В п. 3.2 гл. 2 были введены понятия ковариации двух случайных величин и ковариационной матрицы двумерной случайной величины. Их можно обобщить на случай многомерной случайной величины (случайного вектора).
Определение 5.1.3. Матрицей ковариаций (ковариационной матрицей) случайного вектора X (вектор-столбца) называют матрицу
DX = E[( X −EX)( X −EX)T ],
если все указанные математические ожидания существуют. Заметим, что если X — это вектор-столбец с компонентами X1, …
…, Xn, то произведение ( X −EX)( X −EX)T , т. е. произведение вектор-

198 Глава 3. Некоторые важные распределения вероятностей
столбца на вектор-строку, есть матрица размерности n ×n. Ее элемент с номером (ij) есть произведение двух случайных величин ( Xi −EXi)( Xj −EXj ). Каждый из этих сомножителей показывает отклонение (вариацию) соответствующей случайной величины от своего среднего значения, а их произведение — совместное отклонение, или совместную вариацию. Среднее значение (или, другими словами, математическое ожидание) этой совместной вариации и называется матрицей ковариаций. Итак, элементы матрицы ковариаций — это не что иное, как ковариации Cov( Xi, Xj ) = E( Xi −EXi)( Xj −EXj ) компонент вектора X. При этом диагональные элементы матрицы DX — это дисперсии случайных величин X1, …, Xn.
Заметим, что DX — симметричная и неотрицательно определенная матрица и что
DX = E( XX T ) −(EX)(EX)T .
Теорема 5.1.2 (Без доказательства). Пусть X, Y — статистически независимые случайные векторы (столбцы) одной размерности, A, b — постоянные (не случайные) матрица и вектор. Тогда
D( X +Y ) = DX +DY , D( AX +b) = A(DX) AT ,
если указанные матрицы ковариаций DX, DY существуют.
Первое из утверждений этой теоремы обобщает на случайные векторы и практически просто является следствием уже известного нам свойства дисперсии суммы независимых случайных величин.
В качестве частного случая второго утверждения теоремы рассмотрим скалярное произведение неслучайного вектора a и случайного вектора X (оба столбцы). Результатом такого произведения является взвешенная сумма a1 X1 +a2 X2 +… +an Xn. Ее можно также рассматривать как произведение матрицы aT (состоящей из одной строки) и вектор-столбца X — это aT X. Применительно к aT X теорема 5.1.2 принимает вид
D(aT X) = aT (DX)a.
5.2. Гауссовские (нормально распределенные) векторы
Из всех многомерных (совместных) распределений самым важным и практически используемым является класс распределений, называемых многомерными нормальными распределениями. Эти распределения являются естественным обобщением на случай нескольких измерений нормальных распределений на числовой прямой. Ввести (определить) многомерные нормальные распределения можно разными способами.
§ 5. Многомерное нормальное распределение |
199 |
|
|
Мы выбрали путь, которым шли при определении одномерных нормальных распределений, т. е. нормальных распределений вероятности на числовой прямой. (Напомним, что при этом сначала вводилась стандартная нормальная случайная величина Z, а от нее осуществлялся линейный переход к произвольной нормальной случайной величине X =a +σZ.)
Ив многомерном случае мы поступим аналогичным образом.
Аименно, мы начнем с того, что определим многомерную стан-
дартную нормальную случайную величину. Точнее говоря, мы определим многомерные стандартные нормальные случайные величины, свою для каждой размерности. Распределение, которое в пространстве соответствующей размерности задает многомерная стандартная нормальная величина, называют многомерным стандартным нормальным распределением. Многомерными нормальными случайными величинами называют произвольные линейные функции от многомерных стандартных нормальных случайных величин. Наконец, многомерными нормальными распределениями называют распределения вероятностей, которые (в пространствах соответствующих размерностей) задают определенные таким образом многомерные нормальные случайные величины.
Стандартные нормальные случайные величины. Пусть Z1 , Z2 , …, Zm
(m ¾1 — произвольное натуральное число) суть независимые случайные величины, распределенные по стандартному нормальному закону N(0, 1).
Определение 5.2.1. Вектор (столбец)
Z = (Z1, …, Zm)T |
(5.2.1) |
называют m-мерным стандартным нормальным (гауссовским) вектором.
В пространстве Rm случайный вектор Z задает распределение вероятностей, называемое m-мерным стандартным нормальным распределением.
Рассмотрим линейные функции векторов (5.2.1):
X = a +BZ, |
(5.2.2) |
где a — постоянный (не случайный) вектор (столбец), B — постоянная (не случайная) матрица. Размерности матриц a, B, Z должны быть согласованными в том смысле, чтобы указанные в формуле (5.2.2) действия были возможны. В частности, векторы X, a и BZ должны иметь одинаковые размерности. Обозначим эту размерность

200 Глава 3. Некоторые важные распределения вероятностей
d, d ¾1. Заметим, что размерность d есть ни что иное, как число строк в неслучайной матрице B.
Определение 5.2.2. Вектор (столбец) X, заданный (5.2.2), называют d-мерным нормальным (гауссовским) вектором.
В пространстве Rd случайный вектор X задает распределение вероятностей, называемое d-мерным нормальным распределением.
Замечание 1. Данное многомерное нормальное распределение с помощью формул вида (5.2.2) может быть задано не единственным способом: одно и то же многомерное нормальное распределение можно получить с помощью разных векторов Z и матриц B.
Замечание 2. Принятое определение многомерного нормального распределения не вступает в противоречие с известным определением одномерного нормального распределения: если определенный формулой (5.2.1) случайный вектор X оказывается одномерным, т. е. если линейная комбинация (5.2.1) задает случайную величину, то распределение этой случайной величины является нормальным в силу доказанного ранее свойства нормального распределения (линейная комбинация независимых гауссовских случайных величин имеет гауссовское распределение).
Если говорить кратко, то нормальные векторы — это аффинные преобразования стандартных нормальных векторов, а многомерные нормальные распределения — это распределения в многомерных пространствах, которые задают эти нормальные векторы.
Непосредственно из определения (5.2.2) и свойств линейных функций вытекает теорема.
Теорема 5.2.1. Любая линейная функция гауссовского случайного вектора является гауссовским случайным вектором.
Для доказательства достаточно вспомнить, что суперпозиция линейных функций является линейной функцией, а поэтому линейная функция от вектора X, заданного (5.2.2), сама имеет вид (5.2.2) — с другими a, B (и, возможно, другой размерностью d).
Следствие 1. Частные распределения случайного гауссовского вектора являются гауссовскими. Так, для гауссовского случайного вектора X = ( X1, …, Xd)T маргинальные распределения случайных величин X1, …, Xd являются гауссовскими.
Следствие 2. Пусть случайные величины X и Y имеют совместное нормальное распределение. Тогда случайная величина X +Y тоже имеет нормальное распределение.
(Ранее доказанная теорема о том, что сумма независимых гауссовских случайных величин распределена нормально, является частным случаем этого следствия.)
