
tjurin_teorija_verojatn_978-5-94057-540-5_1
.pdf§ 1. Случайные величины и их распределения |
101 |
|
|
Поэтому для этих случайных величин составлены специальные таблицы значений функций распределения. С помощью этих таблиц легко вычислить вероятности попадания случайных величин в те или иные интервалы значений, используя выражение (1.4.1). В последнее время многие компьютерные программы включают в себя вычисление значений функций распределений наиболее распространенных случайных величин. Как это делает EXCEL, будет рассказано в гл. 3.
Упражнения
Для следующих случайных величин постройте графики их функций распределения вероятностей.
1.Случайная величина X — число орлов при трех подбрасываниях правильной монеты.
2.Правильную игральную кость бросают дважды. Случайная величина X — наибольшее число очков, выпавшее за два броска.
3.Случайный эксперимент заключается в случайном выборе точки внутри круга радиуса R (предполагается, раз речь идет о случайном выборе, что вероятность попасть в любую замкнутую область круга пропорциональна площади этой области). Определим случайную величину X как расстояние от выбранной точки до центра круга. Найдите функцию распределения этой случайной величины.
4.Пусть X — число орлов при 30 подбрасываниях правильной мо-
неты. Выпишите в виде суммы отдельных слагаемых значение FX (10). Оцените, какие вычислительные усилия требуются для нахождения значения FX (10). Возрастут ли эти усилия при вычислении FX (15)?
5.Пусть X — число орлов при 30 подбрасываниях правильной монеты. В таблице 2.5 приведены некоторые значения функции распределения этой случайной величины с точностью до четырех значащих цифр после запятой.
|
|
|
|
|
|
Таблица 2.5 |
|
|
|
|
|
|
|
|
|
значения x |
9 |
13 |
15 |
17 |
20 |
23 |
|
|
|
|
|
|
|
|
|
вероятности FX (x) |
0,0214 |
0,2923 |
0,5722 |
0,8192 |
0,9786 |
0,9993 |
|
|
|
|
|
|
|
|
|
Найдите вероятности следующих событий:
а) P( X >23). Можно ли считать это событие маловероятным?
б) P(9 < X ¶20). Можно ли считать это событие практически достоверным?
в) P(13 < X ¶17).
6. Двое играют в следующую игру. Правильная монета подбрасывается 30 раз. Если при этом число выпавших орлов больше 13, но
102 |
Глава 2. Случайные величины |
|
|
меньше 18, выигрывает первый, в противном случае — второй. Одинаковы ли у игроков шансы на выигрыш? (Используйте данные из таблицы 2.5.)
С помощью функции распределения F( x) непрерывной случайной величины X выразите вероятности следующих событий.
7. P( X >a).
8.P(|X|<b).
9.P(|X|>b).
§2. Числовые характеристики случайных величин
Выше мы выяснили, что любая случайная величина порождает функцию распределения. Эта функция удобна для вычисления вероятностей различных событий, но одновременно может быть довольно громоздка, так как для практических целей часто возникает необходимость знать ее значения во многих точках. Поэтому, наряду с подробными описаниями функций распределения, стремятся охарактеризовать случайную величину всего несколькими числами. Эти числовые характеристики функций распределения одновременно дают представление и о поведении случайной величины, и их также называют числовыми характеристиками случайных величин.
Наиболее часто употребляемыми характеристиками случайной величины (и соответствующего распределения вероятностей) служат моменты и квантили. Ниже мы их определим, но надо сделать оговорку: универсальные (пригодные для любых случайных величин) определения этих характеристик требуют более сложного математического аппарата, чем тот, который мы используем в этой книге. Поэтому этих общих определений мы приводить не будем. Вместо этого мы дадим более простые определения для дискретных и для непрерывных случайных величин отдельно.
2.1. Математическое ожидание
Начнем с так называемого первого центрального момента случайной величины X, называемого также математическим ожиданием или средним значением X. Его обозначают через MX или EX. В этой книге мы будем использовать обозначение EX. Символ E в обозначении математического ожидания EX происходит от английского слова expectation, означающего ожидание. Первоначально термин математическое ожидание был введен для определения ожидаемого (среднего) выигрыша в многократно повторяемой игре. В дальнейшем оказа-
§ 2. Числовые характеристики случайных величин |
103 |
|
|
лось, что это понятие удобно для характеристики положения «центра» распределения многих случайных величин.
2.1.1. Определение и примеры.
Определение 2.1.1. Математическим ожиданием дискретной случайной величины X называют сумму всех возможных произведений вида x · P( X = x), где x обозначает возможное значение случайной
величины X. В виде формулы это определение можно записать как
X
EX = x ·P( X = x),
x
причем суммирование идет по всем возможным значениям случайной величины.
Если множество возможных значений величины X конечно, то EX всегда существует и не зависит от порядка суммирования. Если это множество бесконечное (счетное), то речь идет о сумме бесконечного ряда значений. Эта сумма может и не существовать, и тогда говорят, что у случайной величины нет математического ожидания.
Условие независимости результата от порядка суммирования выступает как дополнительное требование к распределению случайной величины X для того, чтобы существовало математическое ожидание.
Если возможные значения дискретной случайной величины X занумерованы и распределение X представлено таблице 2.4, то формула для ее математического ожидания упрощается. В этом случае определение 2.1.1 превращается в следующее определение.
Определение 2.1.2. Для дискретной случайной величины X со значениями x1, x2, …, имеющими вероятности p1, p2 , …, математическое ожидание определяется формулой
EX = Xk |
xk pk. |
Для бесконечного, счетного числа возможных значений X необ- |
|
ходимым и достаточным условием существования математического
ожидания служит требование абсолютной сходимости ряда, т. е. дол- |
|
жен сходиться ряд Pk |
|xk|pk. |
Определение 2.1.3. Для непрерывной случайной величины X |
|
с плотностью вероятности p( x) математическое ожидание определя-
ется формулой
Z∞
EX = xp( x) dx,
−∞
причем интеграл должен сходиться абсолютно.

104 |
Глава 2. Случайные величины |
|
|
Рассмотрим некоторые примеры на вычисление математических ожиданий.
Пример 1. Случайная величина X — число выпавших очков при бросании одной игральной кости. Возможные значения X — это числа 1, 2, 3, 4, 5, 6; вероятность появления любого из них — одна шестая, если кость правильная. Производя подсчет по формуле из определения 2.1.1, получаем
EX = (1 +2 +3 +4 +5 +6)/6 = 3,5.
Заметим, что это число находится в некотором смысле посредине между возможными значениями случайной величины.
Пример 2. Математическое ожидание числа очков, выпавших при бросании двух игральных костей, можно вычислить по той же формуле. Распределение этой случайной величины было дано в п. 1.2 (см. таблицу 2.3). Подсчет дает значение 7.
Но проще и правильней здесь действовать иначе: воспользоваться одним из свойств математического ожидания, которые будут указаны ниже. Пусть X1 — число очков, выпавшее на первой кости, X2 — число очков на второй. Интересующее нас общее число очков — это X1 + X2 , а нужное нам свойство математического ожидания: E( X1 + X2) =EX1 +EX2 ; отсюда вновь получаем значение 7.
Пример 3. Математическое ожидание случайной величины, равномерно распределенной на отрезке [a, b], получаем по формуле из определения 2.1.3:
b
Z |
2 |
2 |
|
||
x |
dx = |
2(b b−−aa) |
= a +2 b . |
||
b −a |
|||||
a
Заметим, что значение a +2 b является серединой отрезка [a, b]. Пример 4. Математическое ожидание для показательного рас-
пределения. Плотность этого распределения указана в п. 1.3, и там же было сказано, что это распределение служит математической моделью случайного срока службы изделия. Вычисления по формуле из определения 2.1.3, получаем
Z∞
θx e−θx dx = θ.
0
Теперь мы можем указать вероятностный смысл параметра θ: это ожидаемое время службы изделия; чем больше θ, тем долговечнее (надежнее) изделие.
§ 2. Числовые характеристики случайных величин |
105 |
|
|
Как говорилось выше, приведенные определения EX не являются исчерпывающими, поскольку пригодны не для всех видов случайных величин. Общее определение математического ожидания выглядит следующим образом:
Z
EX = x dFX ( x),
где FX ( x) — функция распределения вероятностей, порожденного случайной величиной X. Приведенные выше формулы для дискретного и непрерывного распределений являются частными случаями этого выражения. Мы не будем пользоваться общим определением,
ипотому не будем разъяснять, как понимать и вычислять такие интегралы.
Заметим, что существуют распределения вероятностей без математического ожидания. С такими случайными величинами иногда приходится сталкиваться на практике. Простой пример — «игра в орлянку», где двое поочередно бросают правильную монету. Если выпадает герб, выигрывает игрок A, если решка — игрок B. Неожиданная (на первый взгляд) черта этой игры состоит в том, что в выигрыше практически постоянно находится один игрок. Впрочем, с вероятностью 1 когда-нибудь наступит и момент ничьей. Так вот, случайное время (число партий) до наступления первого ничейного момента не имеет математического ожидания. Математическое ожидание этой случайной величины бесконечно.
Можно дать и более формальный пример: пусть случайная величина X принимает значения 11 , 22, …, nn, … с вероятностями 2−1 , 2−2
ит. д. Эта случайная величина не имеет математического ожидания.
2.1.2.Свойства математического ожидания. Перечислим с пояснениями, но без детального доказательства основные свойства математического ожидания.
1. Математическое ожидание постоянной равно этой постоянной. Постоянную величину можно рассматривать как вырожденный случай дискретной случайной величины, т. е. как случайную величину, которая принимает лишь одно значение с вероятностью единица. Ясно, что никакой случайности при этом не наблюдается. Указанное свойство вытекает прямо из определения математического ожидания. Его упоминают потому, что случайные величины на практике часто приходится преобразовывать, и надо уметь вычислять математические ожидания преобразованных случайных величин.
106 |
Глава 2. Случайные величины |
|
|
2. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий, т. е.
E( X +Y ) = EX +EY .
Это совсем не очевидное свойство. На примере суммы числа очков при двукратном бросании игральной кости мы видели, что распределение суммы случайных величин (в данном случае числа очков, выпавших при первом и втором броске) отличается от исходных распределений каждой из случайных величин. Вычислить математическое ожидание числа очков на одной игральной кости совсем просто. А вот вычисление математического ожидания суммы числа очков при двукратном бросании кости требует несколько больших усилий, если действовать по определению. Сначала надо вычислить распределение суммы, а потом считать само математическое ожидание.
3. Математическое ожидание произведения случайной величины на константу равно произведению этой константы на математическое ожидание случайной величины, т. е.
E(aX) = aEX.
(Другими словами, постоянный множитель можно выносить за знак математического ожидания.) Это свойство следует прямо из определения. Все возможные значения случайной величины aX получаются путем умножения значений исходной случайной величины на константу a. При этом вероятности этих значений (или плотность распределения) не меняются. Сформулированное свойство — следствие того, что постоянный множитель можно вынести как за знак суммы (для дискретной случайной величины), так и за знак интеграла (для непрерывной случайной величины).
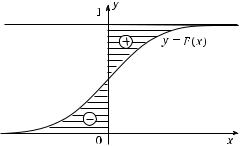
Полезно иметь в виду следующее геометрическое толкование математического ожидания. Пусть F( x) — функция распределения слу-
Рис. 2.7. Геометрическая интерпретация математического ожидания
§ 2. Числовые характеристики случайных величин |
107 |
|
|
чайной величины X. Тогда EX равно разности площадей, заключенных между осью ординат, прямой y =1 и кривой y =F( x) в интервале (0, +∞), и между осью абсцисс, кривой y = F( x) и осью ординат в промежутке (−∞, 0) (см. рис. 2.7). Это правило позволяет во многих случаях находить математическое ожидание почти без вычислений, используя различные свойства функции распределения.
Упражнения
1.Во многих детских играх для передвижения по игровому полю используется игральная кость. Фишка передвигается на число полей, равное числу очков, выпавшему на игральной кости. На сколько полей в среднем продвинется один игрок за десять ходов? Другими словами, чему равно математическое ожидание суммы числа очков при десятикратном бросании игральной кости?
2.Случайные величины X и Y имеют равномерное распределение вероятностей на отрезке [0, 1]. Вычислите математическое ожидание случайной величины X +Y . Найдите плотность распределения веро-
ятности X +Y . (Эта задача является непрерывным аналогом задачи о математическом ожидании числа очков, выпавших при одном
идвух бросках игральной кости. Заметим, что если найти плотность распределения суммы двух равномерно распределенных случайных величин относительно просто, то переход к сумме трех, четырех
ит. д. подобных случайных величин поиск плотности усложняет. Однако благодаря свойствам математического ожидания вычисление математического ожидания суммы нескольких равномерно распределенных случайных величин остается простой задачей.)
2.2. Дисперсия
Кроме среднего значения случайной величины, которое в определенном смысле характеризует центр распределения вероятностей, представляет интерес и разброс случайной величины относительно этого центра. Для характеристики (количественного описания) данного разброса в теории вероятностей используют второй центральный момент случайной величины. В русскоязычной литературе его называют дисперсией и обычно обозначают DX. В англоязычной литературе используется термин вариация, и дисперсию обозначают
Var( X).
Определение 2.2.1. Дисперсией DX случайной величины X называется величина
DX = E( X −EX)2 . |
(2.2.1) |

108 |
Глава 2. Случайные величины |
|
|
Дисперсия, так же как и математическое ожидание, существует не для всех случайных величин (не для всех распределений вероятностей).
Выражение, стоящее под знаком математического ожидания в определении дисперсии, можно преобразовать, воспользовавшись свойствами математического ожидания:
DX = E( X −EX)2 = E( X2 −2 XEX +(EX)2) = EX2 −(EX)2. (2.2.2)
Формулу (2.2.2) удобнее использовать для вычисления дисперсии случайных величин в практических задачах.
Пример 1. Пусть X — число выпавших очков при бросании одной игральной кости. Дисперсия этой случайной величины может быть легко рассчитана по формуле (2.2.2). Для этого надо вычислить математическое ожидание случайной величины X2 . Эта случайная величина может принимать значения 1, 4, 9, 16, 25, 36 с одинаковой вероятностью 1/6 для каждого из них. Следовательно,
EX2 = 16 (1 +4 +9 +16 +25 +36) = 916 ≈ 15,17,
DX = EX2 −(EX)2 = 916 −(3,5)2 = 2 1112 ≈ 2,92.
Пример 2. Дисперсия случайной величины, равномерно распределенной на отрезке [a, b], равняется
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
a |
x2 |
a +b |
2 = |
(b −a)2 |
|
|||
|
= |
|
|
= |
|
|
|
|
|
|
||||
DX |
|
EX |
|
−(EX) |
|
Z |
b −a dx − |
|
2 |
|
|
12 . |
||
Если необходимо, чтобы показатель разброса случайной величины выражался в тех же единицах, что и значение этой случайной величины, то вместо DX используют величину pDX , которая называется
средним квадратическим отклонением, или стандартным отклонением случайной величины X.
2.2.1. Свойства дисперсии. Из свойств дисперсии отметим следующие:
1.Дисперсия постоянной величины равна нулю.
2.Для любой неслучайной постоянной a выполняется равенство
D( X +a) = D( X), D(aX) = a2 D( X).
Упражнения
Для следующих случайных величин вычислите их математическое ожидание и дисперсию.

§ 2. Числовые характеристики случайных величин |
109 |
|
|
1.Случайная величина X может принимать только два значения: 1 и 0 с вероятностями p и q =1 −p соответственно (0 < p <1).
2.Случайная величина X — число орлов при двух подбрасываниях правильной монеты.
3.Правильную игральную кость бросают дважды. Случайная величина X — наибольшее число очков, выпавшее за два броска.
4.Случайная величина X имеет симметричную плотность распределения вероятностей p(t), т. е. для любого t справедливо равенство p(t) = p(−t). Докажите, что EX =0.
5.Случайная величина X имеет стандартное нормальное распределение вероятностей, т. е. плотность распределения вероятностей этой случайной величины есть
p(t) = p1 e−t22 .
2π
Вычислите EX.
2.2.2. Моменты. Кроме первого и второго моментов при описании случайных величин иногда используются и другие моменты: третий, четвертый и т. д. Мы дадим их определения отдельно для дискретных и для непрерывных случайных величин.
Определение 2.2.2. |
Для дискретной случайной величины X со |
||||||||||
значениями |
x1 |
, x2, … , имеющими вероятности p1 , p2, … , k-м мо- |
|||||||||
ментом EX k |
называется величина EX k = |
xk p , а k-м центральным |
|||||||||
моментом называется величина |
( xi |
PiEXi)k ipi. Для непрерывной |
|||||||||
случайной величины с плотностьюPi p( x)−, k-м моментом называется |
|||||||||||
∞ |
|
|
p |
|
x |
k = |
∞ |
|
k |
|
|
−R∞ x |
k |
|
|
|
|
||||||
величина |
|
|
( |
) dx, а |
k-м центральным моментом называется |
||||||
величина E( X −EX) |
|
R( x −EX) |
|
p( x) dx. |
|||||||
−∞
Чтобы приведенные формулы имели смысл, требуется, чтобы суммы и интегралы сходились абсолютно. Так же как математическое ожидание и дисперсия, моменты существуют не у всех случайных величин.
2.2.3. Асимметрия и эксцесс. В отличие от обычных моментов, центральные моменты не меняются при прибавлении к случайной величине постоянного слагаемого, т. е. они не зависят от выбора начала отсчета в шкале измерения случайной величины. Но от выбранной единицы измерения зависимость остается: если, скажем, случайную величину начать измерять не в метрах, а в сантиметрах, то значения центральных моментов также изменятся. Иногда это бывает неудобно. В таких случаях, чтобы устранить подобное влияние,

110 |
Глава 2. Случайные величины |
|
|
моменты тем или иным способом нормируют, например, деля их на соответствующую степень среднего квадратического отклонения. В результате получается безразмерная величина, не зависящая от выбора начала отсчета и единиц измерения исходной случайной величины.
Чаще всего из нормированных моментов используются коэффициенты асимметрии и эксцесса — соответственно третий и четвертый нормированные центральные моменты. Для случайной величины X:
коэффициент асимметрии = E( X −EX )3 ,
(DX )3/2
E( X −EX )4
коэффициент эксцесса = 2 −3.
(DX )
При расчете коэффициента эксцесса тройку вычитают для того, чтобы коэффициент эксцесса нормального распределения оказался равным 0. (Об этом важном распределении см. далее в гл. 3.)
Принято считать, что коэффициент асимметрии в какой-то степени характеризует несимметричность распределения случайной величины, а коэффициент эксцесса — степень выраженности «хвостов» распределения, т. е. частоту появления удаленных от среднего значений. Иногда значения коэффициентов асимметрии и эксцесса используют для проверки гипотезы о том, что наблюденные данные (выборка) принадлежат заданному семейству распределений, например нормальному.
2.2.4. Квантили. Для случайных величин, принимающих значения на числовой прямой, часто используются такие характеристики, как квантили.
Определение 2.2.3. Квантилью xp случайной величины, имеющей функцию распределения F( x), называется решение xp уравнения
F( x) = p.
Напомним, что по определению F( x) =P( X ¶x), т. е. для нахождения квантили надо решить уравнение
P( X ¶ xp) = p
относительно неизвестного xp. Таким образом, квантилью случайной величины называется такое значение xp, что вероятность не превысить его равна p.
Величину xp часто называют p-квантилью или квантилью уровня p распределения F( x). Среди квантилей чаще всего используются медиана и квартили распределения.
Медианой называется квантиль, соответствующая значению p =0,5, т. е. медиана x0,5 — это такая точка распределения случайной величины, что последняя с одинаковой вероятностью принимает б´ольшие и меньшие значения, чем x0,5 .
