
tjurin_teorija_verojatn_978-5-94057-540-5_1
.pdf
§ 3. Несколько случайных величин |
121 |
|
|
Для независимых случайных величин можно пополнить список свойств математического ожидания и дисперсии: если случайные величины X и Y независимы, то:
EXY = (EX) ·(EY ). |
(3.3.1) |
Сразу из этого следует, что Cov( X, Y ) =0, а потому D( X +Y ) =DX +DY при условии, что указанные моменты существуют.
Мы можем доказать свойство (3.3.1) для дискретных случайных величин и для случайных величин, имеющих совместную плотность. Для таких случайных величин формулы для EXY были даны выше. При обращении к этим формулам надо вспомнить, что для независимых случайных величин X и Y выполняются равенства P( X = xi, Y = yj ) =
= P( X = xi)P(Y = yj ) для вероятностей и p( x, y) = f ( x)g( y) для плотностей. Приведем доказательство только для дискретных величин X
и Y , поскольку для непрерывных оно практически повторяется слово в слово — с заменой сумм интегралами. Итак,
EXY = XXi j |
xi yj pij = XXi j |
xi yj P( X = xi)P(Y = yj ) = |
= (EX)(EY ). |
|||
|
= |
• i |
xi P( X = xi)‹• j |
yj P(Y = yj )‹ |
||
|
|
X |
|
X |
|
|
Упражнения
1.Плотность распределения пары случайных величин ( X, Y ) является ненулевой константой на квадрате [0, 1] ×[0, 1] и равна нулю для всех остальных точек числовой плоскости. Можно ли считать случайные величины X и Y независимыми?
2.Плотность распределения пары случайных величин ( X, Y ) является ненулевой константой на квадрате [0, 1] ×[0, 1] и равна нулю для всех остальных точек числовой плоскости. Найдите дисперсию случайной величины X +Y .
3.Плотность распределения пары случайных величин ( X, Y ) задана на всей числовой плоскости следующим образом:
1 x2 + y2 p( x, y) = 2π exp − 2 .
Можно ли считать случайные величины X и Y независимыми? Найдите дисперсию случайных величин X +Y и ( X +Y )/2.
4. Найдите дисперсию суммарного числа очков, выпавших при двукратном бросании игральной кости.

122 |
Глава 2. Случайные величины |
|
|
3.4. Коэффициент корреляции
Из формулы (3.3.1) можно увидеть, что обращение в нуль ковариации является необходимым условием независимости случайных величин (если вторые моменты существуют). Вообще говоря, равенство нулю ковариации не обеспечивает независимости случайных величин. Но есть важное исключение: совместно нормально распределенные случайные величины. Об этом подробно будет сказано в следующем пункте настоящего параграфа.
Для случайных величин, которые не являются независимыми, желательно иметь численную меру, выражающую их взаимную зависимость и взаимосвязь. Сразу заметим, что различие между совместным распределением и произведением маргинальных распределений (это совместное распределение в случае независимости) — объект слишком сложный, чтобы его можно было адекватно выразить одним числом или даже несколькими числами. Все же некоторые показатели такого рода могут быть полезны. Остановимся на наиболее употребительном из них, основанном на свойстве ковариации обращаться в нуль для независимых случайных величин.
Использование самой ковариации в качестве меры связи случайных переменных неудобно, так как величина ковариации зависит от единиц измерения, в которых измерены случайные величины. При переходе к другим единицам измерения (например, от метров к сантиметрам) ковариация тоже изменяется, хотя степень связи случайных переменных, естественно, остается прежней. Поэтому в качестве меры связи признаков обычно используют другую числовую величину, называемую коэффициентом корреляции.
Определение 3.4.1. Коэффициентом корреляции случайных величин X и Y (обозначение Corr( X, Y ), либо ρ( X, Y ), либо просто ρ) называют
Cov( X , Y )
ρ = p p .
DX DY
Заметим, что для существования коэффициента корреляции необходимо (и достаточно) существование дисперсий DX >0, DY >0.
Свойства коэффициента корреляции. Отметим следующие свойства коэффициента корреляции.
1.Модуль коэффициента корреляции не меняется при линейных преобразованиях случайных переменных: |ρ( X, Y )| = |ρ( X′, Y ′)|, где X′ =a1 +b1 X, Y ′ =a2 +b2 Y , a1 , b1, a2, b2 — произвольные числа.
2.Справедливо неравенство |ρ( X, Y )|¶1.
§ 3. Несколько случайных величин |
123 |
|
|
3.Равенство |ρ( X, Y )|=1 достигается тогда и только тогда, когда случайные величины X и Y линейно связаны, т. е. существуют такие числа a, b, что
P(Y = aX +b) = 1.
4.Если X и Y статистически независимы, то ρ( X, Y ) =0. Уже отмечалось, что обратное заключение, вообще говоря, неверно. Об этом мы еще будем говорить.
Свойства 1 и 4 проверяются непосредственно. Докажем свойства 2 и 3 (при желании читатель может эти доказательства пропустить). Пусть t — переменная величина в смысле математического анализа. Рассмотрим дисперсию случайной величины D(Y −tX ) как функцию переменной t. По свойствам дисперсии D(Y −tX ) =t2 DX − −2t Cov( X , Y ) +DY , т. е. дисперсия представляется квадратным трехчленом от t. Этот квадратный трехчлен неотрицателен, поскольку дисперсия всегда неотрицательна. Поэтому для его дискриминанта справедливо равенство [Cov( X , Y )]2 −DXDY ¶0, а это и означает, что |ρ( X , Y )|¶1 (свойство 2).
Для доказательства свойства 3 заметим, что при |ρ( X , Y )|=1 дискриминант приведенного выше квадратного трехчлена обращается в 0, а поэтому при некотором t0 значение D(Y −t0 X ) равно нулю. Равенство нулю дисперсии означает, что эта случайная величина постоянна, т. е. для некоторого c вероятность события (Y −t0 X =c) равна единице, что и требовалось доказать.
Итак, корреляция случайных величин принимает значения от −1 до 1; она может быть равна ±1, только если эти величины линейно зависят друг от друга. Значения корреляции, близкие к −1 или 1, указывают, что зависимость случайных величин друг от друга почти линейная. Значения ковариации, близкие к нулю, означают, что связь между случайными величинами либо слаба, либо не носит линейного характера.
Существует много других показателей для связи случайных переменных и других коэффициентов корреляции, не столь известных, как описанный выше. (Для различения этот коэффициент корреляции называют также коэффициентом корреляции Пирсона, классическим коэффициентом корреляции и т. д.)
Понятие корреляции как меры линейной связи играет в настоящее время фундаментальную роль в прикладных исследованиях. Для практики важно знать, есть ли какая-то взаимосвязь между одновременно измеряемыми показателями, если они подвержены случайной изменчивости. Можно ли считать эти показатели независимыми? Если зависимость есть, то насколько она сильна?
3.5.Примеры совместных распределений
Втеорией вероятностей для отдельного изучения выведено не так уж много многомерных распределений (в отличие от одномерных, которым посвящена отдельная глава этой книги). Наиболее известные

124 Глава 2. Случайные величины
из них — равномерное и нормальное распределения. Эти распределения уже возникали у нас в упражнениях к предыдущим пунктам. Здесь мы поговорим о них подробнее.
Равномерное распределение на области D задается с помощью плотности. Эта функция плотности принимает всего два значения: 0 вне области D и |D|−1 внутри D, где |D| обозначает площадь области D. Можно было бы просто сказать, что плотность постоянна внутри области D. Тогда ее значение |D|−1 определилось бы тем, что интеграл плотности по всему пространству равен 1.
Пусть ( X, Y ) — пара случайных величин, равномерно распределенная в области D. Рассмотрим два простых примера области D.
Пусть D — прямоугольник с центром (a, b), стороны которого параллельны координатным осям. В этом случае случайные переменные X и Y независимы, EX =a, EY =b.
Пусть теперь D — круг с центром (a, b). Покажите, что EX = a, EY = b, Cov( X, Y ) = 0, но случайные переменные X и Y взаимно зависимы.
Нормальное распределение. Рассмотрим пару случайных величин ( X, Y ), и пусть ρ — коэффициент корреляции между X и Y . Введем следующие обозначения для математических ожиданий и дисперсий случайных величин X и Y : µx =EX, σ2x =DX, µy =EY , σ2y =DY .
Определение 3.5.1. Распределение пары случайных величин ( X, Y )
называют нормальным или двумерным нормальным, если их совместная плотность p( x, y) задается формулой
p( x, y) |
= |
1 |
|
|
|
|
× 2 |
|
|
|
|
|
|
|
|
2πσx σy p |
|
|
|
|
|
|
|
|
|
||||||
1 −ρ2 |
|
− |
|
σx σy |
σ2y |
2 |
˜ª |
||||||||
× |
|
§−2(1 −ρ2 ) • |
σ2x |
|
|
||||||||||
|
exp |
|
1 |
|
|
(x −µx ) |
|
2ρ |
(x −µx )( y −µy ) |
+ |
( y −µy ) |
|
. (3.5.1) |
||
|
|
|
|
|
|
|
|
|
|
||||||
Частные (маргинальные) распределения переменных X и Y тоже нормальные (одномерные) с параметрами, указанными выше.
Ранее мы отметили, что для независимых случайных величин коэффициент их корреляции равен 0. Для случайных величин, имеющих совместное нормальное распределение, верно и обратное заключение: случайные величины X и Y независимы, если ρ=0. (Из формулы (3.5.1) легко увидеть, что совместная плотность в этом случае превращается в произведение маргинальных плотностей.)
Глава 3
Некоторые важные распределения вероятностей
Вступление. Подчиняются ли каким-то законам явления, носящие случайный характер? Да, но эти законы отличаются от привычных нам физических законов. Значения случайных величин невозможно предугадать даже при полностью известных условиях эксперимента,
вкотором они измеряются. Мы можем лишь указать вероятности того, что случайная величина принимает то или иное значение или попадает в то или иное множество. Зато, зная распределения вероятностей интересующих нас случайных величин, мы можем делать выводы о событиях, в которых участвуют эти случайные величины. Правда, эти выводы будут также носить вероятностный характер.
Среди всех вероятностных распределений есть такие, которые используются на практике особенно часто. Эти распределения детально изучены, и свойства их хорошо известны. Многие из этих распределений лежат в основе целых областей знания, таких как теория массового обслуживания, теория надежности, контроль качества, теория измерений, теория игр и т. п. В этой главе мы расскажем о некоторых из таких распределений, покажем типичные ситуации, в которых они необходимы, выведем их основные числовые характеристики, дадим описания наиболее распространенных таблиц распределений и правил их использования. Кроме того, будет рассмотрено компьютерное моделирование различных распределений и расчет вероятностей различных событий с помощью пакета EXCEL.
Большинство применяемых на практике распределений являются дискретными или непрерывными. Среди дискретных распределений будут рассмотрены биномиальное и пуассоновское, среди непрерывных — показательное и нормальное. Мы не включили в эту книгу ряд важных статистических распределений: Стьюдента, хи-квадрат и F- распределение Фишера, так как рассказ о них требует обсуждения типичных статистических задач (см. [26]) и более сложных технических средств. На наш взгляд, эти распределения уместней рассматривать
вкурсах математической статистики.

126 Глава 3. Некоторые важные распределения вероятностей
Более подробное изложение свойств этих и многих других распределений можно найти в книгах [4], [15], [18], [21] и [32].
§1. Биномиальное распределение
1.1.Определение и основные свойства
Биномиальное распределение — это одно из самых распространенных дискретных распределений, оно служит вероятностной моделью для многих явлений.
Биномиальное распределение своим возникновением обязано испытаниям Бернулли. Напомним, что испытания Бернулли — это случайный эксперимент, который оканчивается одним из двух возможных исходов. Один из этих исходов условно называют «успехом», другой — «неудачей». Вероятность «успеха» обозначается буквой p, вероятность «неудачи» — буквой q. Ясно по смыслу, что 0 ¶p ¶1, 0 ¶q ¶1
иp + q =1. Числа 0 и 1 как возможные значения для вероятностей «успеха» и «неудачи» включены ради формальных удобств. (Если p =0 или p =1, то исход испытаний Бернулли не случаен.) Более подробно об испытаниях Бернулли говорилось в п. 3.2 гл. 1.
Последовательность независимых испытаний Бернулли, вероятность успеха (и неудачи) в которых остается неизменной, называют также схемой испытаний Бернулли, серией испытаний Бернулли
ит. д. В подобных испытаниях исследователей обычно интересует величина X — «число успехов в серии из n испытаний Бернулли», когда вероятность успеха равна p. Ясно, что величина X — случайная, она может принимать, вообще говоря, любые целые значения от 0 до n включительно. Ее распределение вероятностей является биномиальным.
Определение 1.1.1. Случайная величина X имеет биномиальное распределение с параметрами n (n — натуральное число) и p, 0 ¶p ¶1, если она принимает значения 0, 1, …, n с вероятностями
P( X = k) = Cnk pk(1 −p)n−k для k = 0, 1, …, n. |
(1.1.1) |
Распределение (1.1.1) называют биномиальным, потому что вероятности P( X =k) являются слагаемыми бинома Ньютона:
Xn Xn
1n = ( p +q)n = Cnk pk(1 −p)n−k = P( X = k).
k=0 k=0
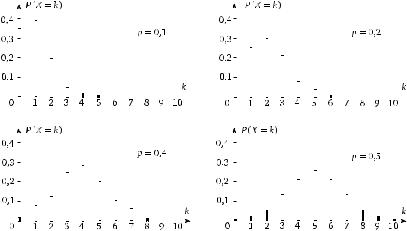
|
|
|
|
|
|
|
§ 1. Биномиальное распределение |
127 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.1. Вид биномиального распределения для различных значений p при n =10
Чтобы подчеркнуть зависимость вероятности события ( X =k) от n и p, его часто записывают в виде
P( X = k) = P( X = k | n, p)
На рис. 3.1 показаны вероятности P( X =k) при n =10 для различных значений p (p =0,1, 0,2, 0,4 и 0,5). На графиках видно, что вероятности различных значений X (при одних и тех же n и p) заметно различаются.
Область применения. Биномиальное распределение возникает в тех случаях, когда нас интересует, сколько раз происходит некоторое событие в серии из определенного числа независимых наблюдений (опытов), выполняемых в одинаковых условиях. Можно особо выделить два наиболее характерных типа подобных испытаний: социологические опросы, опирающиеся на простой случайный выбор (более подробно об этом будет сказано в п. 3.4 гл. 4), и выборочный контроль качества продукции. Кроме того, биномиальное распределение возникает в ряде статистических критериев проверки гипотез, самым простым из которых является критерий знаков (см. гл. 3 книги [26]). Поясним сказанное на примере.
Рассмотрим какое-либо массовое производство. Даже во время его нормальной работы иногда изготавливаются изделия, не соответствующие стандарту, т. е. дефектные. Обозначим долю дефектных изделий

128 Глава 3. Некоторые важные распределения вероятностей
в большой партии через p, 0 < p <1. (Мы здесь используем для обозначения этой доли ту же букву p, что и для вероятности успеха. Это не случайно. В п. 1.2 гл. 4 будет показано (теорема Бернулли), что эта доля в больших партиях практически не отличается от вероятности p встретить дефектное изделие, и более того, используется для определения самой этой вероятности.)
Какое именно произведенное изделие окажется негодным, сказать заранее (до его изготовления) невозможно. Для описания подобной ситуации обычно используется следующая математическая модель:
а) каждое изделие с вероятностью p может оказаться дефектным (с вероятностью q =1 −p оно соответствует стандарту); эта вероятность для всех изделий одинакова;
б) появление как дефектных, так и стандартных изделий происходит независимо друг от друга; это значит, что в нормальном процессе производства появление бракованного изделия не влияет на возможность появления брака в дальнейшем; нарушение этого условия означает сбой нормального технологического режима.
Поэтому мы можем перефразировать вышесказанное так: в нормальных условиях технологический процесс производства математически описывается схемой испытаний Бернулли.
Для чего же на производстве требуется подсчитывать число дефектных изделий? Как правило, это делается для контроля технологического процесса. При массовом производстве сплошная проверка качества изготовленных изделий обычно неоправданна. Поэтому для контроля качества из произведенной продукции наудачу отбирают определенное количество изделий (в дальнейшем — n) и проверяют их, регистрируют найденное число бракованных изделий (в дальнейшем — X) и в зависимости от значения X принимают то или иное решение о состоянии производственного процесса. Теоретически X может принимать любые целые значения от 0 до n включительно, но, конечно, вероятности этих значений различны. Для того чтобы делаемые по значению X выводы были обоснованными, требуется знать распределение случайной величины X. Если выполняются приведенные выше условия схемы испытаний Бернулли, то распределение величины X является биномиальным распределением и вероятности значений X можно получить очень просто.
Пронумеруем в произвольном порядке n проверяемых изделий (например, в порядке их поступления на контроль). Будем обозначать исход испытания каждого изделия нулем или единицей (нуль —
§ 1. Биномиальное распределение |
129 |
|
|
нормальное изделие, единица — дефектное) и будем записывать итоги проверки партии из n изделий в виде последовательности из n нулей и единиц. Событие ( X =k), или, другими словами, «среди n испытаний изделий оказалось k бракованных, а остальные n −k — годные» — это совокупность всех последовательностей, содержащих в любом порядке k единиц и n − k нулей. Вероятность того, что в результате проверки будет получена любая из таких последовательностей, равна pk(1 −p)n−k (здесь существенно используется независимость появления годных и негодных изделий (см. п. 3.1 гл. 1)), а число
таких последовательностей — Ck = |
n! |
. Поэтому согласно свой- |
|
||
n |
k!(n −k)! |
|
|
||
ствам вероятностей, описанным в п. 2.2 гл. 1, вероятность события ( X =k) вычисляется по формуле:
P( X = k) = Cnk pk(1 −p)n−k |
= |
n! |
pkqn−k. |
k!(n −k)! |
Об использовании схемы Бернулли и биномиального распределения при расчете размера социологической выборки с заданными свойствами мы подробно расскажем в п. 3.4 гл. 4, когда для этого будут введены необходимые понятия.
На простом, но довольно общем и характерном примере покажем, как используется биномиальное распределение вероятностей в процедурах принятия решений в математической статистике. Пусть нас интересует эффект воздействия некоторого препарата на скорость реакции человека. (С тем же успехом мы могли бы обсуждать эффект воздействия какого-нибудь экономического закона на показатели работы предприятия или эффект информационного воздействия на мнение избирателя.) Экспериментальное измерение скорости реакции одного и того же человека в неизменных условиях показывает, что это величина не постоянная. Она принимает разные значения от опыта к опыту, т. е. является величиной случайной. Как же в подобной ситуации выяснить, наблюдается или нет эффект воздействия препарата? Ведь даже без всякого воздействия измерения скорости реакции одного и того же человека дают то большие значения, то меньшие.
Проводить эти исследования можно по-разному. Одни из таких способов предусматривает формирование относительно небольшой (несколько десятков человек) группы независимых испытуемых. (Условие независимости тут обеспечить довольно просто: во-первых, испытуемые не должны быть связаны между собой (скажем, быть родственниками или заниматься одной и той же специфической деятельностью, в которой существенна скорость реакции), а во-вторых,

130 Глава 3. Некоторые важные распределения вероятностей
в ходе проведения самого эксперимента результаты одного испытуемого не должны влиять на результаты другого.) Затем у каждого испытуемого проводится однократное измерение скорости реакции до и после воздействия. Сравним у каждого испытуемого показатели до и после воздействия. Будем считать, что эксперимент для данного испытуемого закончился успехом, если его скорость реакции после воздействия препарата возросла. Неудача соответствует уменьшению скорости реакции. (Конечно, не исключено, что показания до и после воздействия совпадут. Но при измерениях высокой точности такое случается редко, поэтому если это происходит, то эти наблюдения просто отбрасывают.) Итак, в подавляющем большинстве случаев эксперимент с каждым отдельным испытуемым заканчивается успехом или неудачей. Показания испытуемых независимы. Предположим, что препарат не оказывает никакого воздействия. Это означает, что с равной вероятностью эксперимент с отдельным испытуемым может закончиться как успехом, так и неудачей. Остается посчитать общее число успехов после тестирования всех испытуемых.
При сделанных нами предположениях эта величина будет иметь биномиальное распределение вероятностей с вероятностью успеха p =1/2 и параметром n, равным числу несовпадающих показаний до
ипосле воздействия. Предварительно следует решить (для этого нам
ипонадобится биномиальное распределение), какие значения суммарного числа успехов согласуются со сделанным предположением об отсутствии воздействия (в статистике такое предположение именуют нулевой гипотезой), а какие явно противоречат, и по результатам эксперимента либо согласиться с предположением об отсутствии воздействия, либо его отвергнуть и признать наличие воздействия препарата.
Упражнения
1.Игральную кость бросают 6 раз. Пусть случайная величина X равна числу выпавших шестерок в этом эксперименте. Какое распределение вероятностей имеет случайная величина X? Укажите параметры этого распределения. Вычислите вероятность событий: а) P( X =1); б) P( X =6); в) P( X ¶2).
2.Случайная величина X имеет биномиальное распределение
спараметрами n = 5 и p = 0,5. Какие из перечисленных далее зна-
чений может принимать случайная величина X: −2; −0,3; 0; 0,5; 1;
2; 2,5; 5; 6; 10?
3. В студенческой группе 15 девушек и 5 юношей. Из этой группы случайным образом выбирают 4 студентов. Пусть случайная ве-
