
- •Г.И. Скоморохов
- •Введение
- •Основные физические свойства жидкостей
- •1.1. Определение жидкости
- •1.2. Классификация сил, действующих в жидкости
- •1.3. Основные физические свойства жидкостей
- •Гидростатика
- •2.1. Основные понятия гидростатики
- •2.1.2. Давление абсолютное, избыточное, вакуум
- •2.1.3. Свойства гидростатического давления
- •2.1.4. Основное уравнение гидростатики. Закон Паскаля
- •2.1.5. Поверхности уровня
- •2.2. Дифференциальные уравнения гидростатики
- •2.2.2. Основное дифференциальное уравнение гидростатики
- •2.2.3. Дифференциальное уравнение поверхности
- •2.3. Основные задачи гидростатики
- •2.4. Основное уравнение гидростатики из уравнений Эйлера. Закон распределения давления
- •2.4.1. Геометрическая интерпретация основного уравнения гидростатики
- •2.4.2. Энергетическая интерпретация основного уравнения гидростатики
- •2.5. Применение закона Паскаля в технике
- •2.5.1. Приборы для измерения давления
- •2.5.2. Простейшие гидравлические машины.
- •2.5.1. Приборы для измерения давления
- •2.5.2. Простейшие гидравлические машины. Гидравлический пресс. Мультипликатор
- •2.6. Сила давления на плоскую стенку. Гидравлический парадокс
- •2.7. Центр давления
- •2.8. Сила давления жидкости на криволинейные стенки
- •2.9. Закон Архимеда
- •2.10. Относительное равновесие жидкости
- •2.10.1. Движение сосуда с жидкостью прямолинейно в произвольном направлении с постоянным ускорением
- •2.10.2. Движение сосуда с жидкостью вертикально вниз с постоянным ускорением
- •2.10.3. Равномерное вращение цилиндрического сосуда с жидкостью вокруг вертикальной оси
- •2.10.4. Равновесие жидкости в поле центробежных сил при нулевой или слабой гравитация
- •2.11. Формы поверхностей раздела между жидкостью и газом (паром) в условиях динамической невесомости
- •3. Гидродинамика
- •3.2. Виды движения жидкости
- •3.3. Линия тока и траектория частицы, элементарная струйка
- •3.4. Закон сохранения массы. Расход. Уравнение неразрывности
- •3.5. Живое сечение. Смоченный периметр. Гидравлический радиус
- •3.6. Уравнение количества движения для потока жидкости
- •3.7. Дифференциальные уравнения движения идеальной жидкости в форме уравнений Эйлера
- •3.8. Основное дифференциальное уравнение установившегося движения идеальной жидкости
- •3.9. Уравнение Бернулли для струйки идеальной несжимаемой жидкости
- •3.9.1. Геометрический смысл уравнения Бернулли.
- •3.9.2. Энергетический смысл уравнения Бернулли
- •3.9.1. Геометрический смысл уравнения Бернулли. Трубка Пито
- •3.9.2. Энергетический смысл уравнения Бернулли
- •3.10. Уравнение Бернулли для элементарной струйки вязкой жидкости
- •3.11. Уравнение Бернулли для потока вязкой несжимаемой жидкости
- •3.12. Классификация гидравлических потерь. Гидравлический и пьезометрический уклоны
- •3.13. Применение уравнения Бернулли в технике
- •3.14. Основы гидродинамического подобия
- •3.15. Режимы течения жидкости
- •3.16. Критерий Рейнольдса и гидравлический радиус
- •4. Ламинарное течение жидкости
- •4.2. Расход при ламинарном режиме в круглой трубе. Формула Пуазейля. Коэффициент Кориолиса
- •4.3. Потери на трение. Формула Дарси-Вейсбаха
- •4.4. Влияние теплообмена на профиль скоростей и потери по длине
- •4.5. Начальный участок ламинарного потока
- •4.6. Потери на трение при ламинарном течении в каналах некруглой формы
- •4.7. Ламинарное течение в зазорах
- •4.7.1. Течение через зазор между параллельными стенками под действием умеренного перепада давлений
- •4.7.2. Течение через зазор при больших перепадах давления
- •5. Турбулентное движение жидкости
- •5.1. Пульсация местной скорости в турбулентном потоке
- •5.2. Распределение осреднённых местных скоростей в турбулентном потоке
- •5.3. Гидравлически гладкие и шероховатые трубы
- •5.4. Потери по длине в гидравлически гладких трубах
- •5.6. Влияние шероховатости на потери. График Никурадзе
- •Заключение
- •Библиографический список
- •Оглавление
2.4.1. Геометрическая интерпретация основного уравнения гидростатики
Выделим
в «абсолютно» покоящейся жидкости
произвольные точки
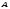 и
и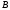 с координатами
с координатами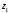 и
и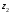 (рис.
2.9). Удалив из трубок с запаянными верхними
концами воздух, погрузим их отвесно в
жидкость так, чтобы нижние открытые их
концы совпали с точками
(рис.
2.9). Удалив из трубок с запаянными верхними
концами воздух, погрузим их отвесно в
жидкость так, чтобы нижние открытые их
концы совпали с точками
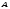 и
и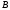 .
.
Под
действием разности давлений жидкость
в трубках поднимется до точек
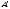 и
и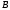 .
Давление в этих точках полагается равным
нулю (хотя в действительности оно будет
несколько выше нуля за счет упругости
паров жидкости и остаточного воздуха
в концах трубки).
.
Давление в этих точках полагается равным
нулю (хотя в действительности оно будет
несколько выше нуля за счет упругости
паров жидкости и остаточного воздуха
в концах трубки).
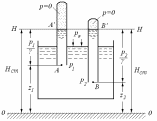
Рис.2.9. Закон распределения давления
в «абсолютно» покоящейся жидкости
Применим
основное уравнение гидростатики (2.10) к
точкам
 и
и
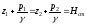 .
.
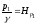 и
и
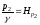 - это высоты столбов жидкости в трубках,
измеренные относительно точек
- это высоты столбов жидкости в трубках,
измеренные относительно точек и
и
 .
Таким образом, точки
.
Таким образом, точки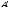 и
и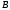 лежат в одной горизонтальной плоскости.
Высотадля
любой точки жидкости
над плоскостью
лежат в одной горизонтальной плоскости.
Высотадля
любой точки жидкости
над плоскостью
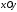 равна сумме высот
равна сумме высот
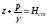 . (2.18)
. (2.18)
В итоге приходим к выводу, что каждый из членов уравнения (2.18) представляет собой некоторую высоту, которым присвоены определенные названия:
 -
геометрическая (или нивелирная) высота;
-
геометрическая (или нивелирная) высота;
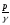 -
пьезометрическая высота;
-
пьезометрическая высота;
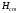 -
высота полного гидростатического
напора.
-
высота полного гидростатического
напора.
Геометрический
смысл
основного уравнения гидростатики. Сумма
геометрической
 и пьезометрической высоты
и пьезометрической высоты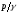 равна полному гидростатическому напору
равна полному гидростатическому напору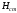 и есть
величина постоянная для всех точек
данной покоящейся массы жидкости.
Пьезометрическая
высота
и есть
величина постоянная для всех точек
данной покоящейся массы жидкости.
Пьезометрическая
высота
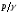 (а с ней и гидростатическое давление
(а с ней и гидростатическое давление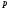 )
может изменяться только ха счёт
соответствующего изменения геометрической
высоты
)
может изменяться только ха счёт
соответствующего изменения геометрической
высоты ,
т.е. при увеличении
,
т.е. при увеличении уменьшается
уменьшается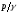 ,
и наоборот.
,
и наоборот.
2.4.2. Энергетическая интерпретация основного уравнения гидростатики
Рассмотрим
потенциальную энергию жидкости в
элементарном объёме, выделенном около
произвольной точки
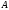 с геометрической высотой
с геометрической высотой и давлением
и давлением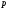 (рис. 2.10).
(рис. 2.10).
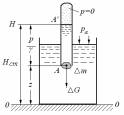
Рис. 2.10. Энергетическая интерпретация
основного уравнения гидростатики
Полная
потенциальная энергия в этом объёме
складывается из двух частей: потенциальной
энергии положения
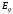 и потенциальной энергии давления
и потенциальной энергии давления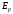 :
:
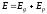 .
.
Первая
из них
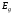 может быть определена как работа, которую
совершила бы сила тяжести
может быть определена как работа, которую
совершила бы сила тяжести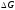 при опускании массы выделенного объёма
жидкости
при опускании массы выделенного объёма
жидкости до уровня плоскости сравнения
до уровня плоскости сравнения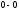 :
:
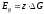 .
.
Вторая
же
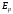 может быть превращена в механическую
работу, на которую можно поднять жидкость,
если в точку
может быть превращена в механическую
работу, на которую можно поднять жидкость,
если в точку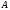 опустить запаянную с одного конца трубку
с удаленным из неё воздухом. Как мы уже
знаем, жидкость поднимется в такой
трубке на высоту
опустить запаянную с одного конца трубку
с удаленным из неё воздухом. Как мы уже
знаем, жидкость поднимется в такой
трубке на высоту ,
следовательно, жидкость, обладая весом
,
следовательно, жидкость, обладая весом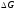 ,
совершит работу
,
совершит работу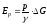 .
.
Таким образом, потенциальная энергия выделенной частицы жидкости
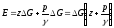 .
.
Отнеся потенциальную энергию к весу жидкости, получим высоту полного гидростатического напора:
 . (2.19)
. (2.19)
Как видим, каждый из членов уравнения (2.19) представляет собой удельную (приходящуюся на единицу веса жидкости) энергию того или иного вида:
 -
удельная потенциальная энергия положения
жидкости;
-
удельная потенциальная энергия положения
жидкости;
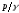 -
удельная потенциальная энергия давления;
-
удельная потенциальная энергия давления;
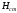 -
полная удельная потенциальная энергия
покоящейся жидкости.
-
полная удельная потенциальная энергия
покоящейся жидкости.
Энергетический
смысл основного
уравнения гидростатики. Сумма
удельной потенциальной энергии положения
 и удельной потенциальной энергии
давления
и удельной потенциальной энергии
давления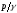 равна полной удельной потенциальной
энергии
равна полной удельной потенциальной
энергии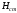 и есть
величина постоянная для всех точек
данной покоящейся массы жидкости.
и есть
величина постоянная для всех точек
данной покоящейся массы жидкости.
Удельная
потенциальная энергии давления
 может изменяться только ха счёт измененияудельной
потенциальной энергия положения жидкости
может изменяться только ха счёт измененияудельной
потенциальной энергия положения жидкости
 .
.
Закон распределения давления в (2.19) можно таким образом рассматривать как частное выражение закона сохранения энергии применительно к непрерывному объёму «абсолютно» покоящейся несжимаемой жидкости, когда один вид энергии переходит в другой, и наоборот.
