Лабораторная работа №1

Линейные интерполяционные полиномы

Цель работы: освоить математический аппарат нахождения линейных интерполяционных полиномов. Практически научиться находить линейные интерполяционные полиномы для одномерного, двумерного и трехмерного симплекс-элемента.

Приближенные формулы и линейная интерполяция

Если задана функция у(х), то это означает, что любому допустимому значению х сопоставлено значение у. Но нередко оказывается, что нахождение этого значения очень трудоемко. Например, у(х) может быть определено как решение сложной задачи, в которой х играет роль параметра, или у(х) измеряется в дорогостоящем эксперименте. При этом можно вычислить небольшую таблицу значений функции, но прямое нахождение функции при большом числе значений аргумента будет практически невозможно.

Функция у(х) может участвовать в каких-либо физико-технических или чисто математических расчетах, где ее приходится многократно вычислять. В этом случае выгодно заменить функцию у(х) приближенной формулой, т.е. подобрать некоторую функцию (х), которая близка в некотором смысле к у(х) и просто вычисляется. Затем при всех значениях аргумента полагают у(х)(х). Близость получают введением в аппроксимирующую функцию свободных параметров а = {а1, а2, ..., аn} соответствующим их выбором.

Пусть функция у(х) известна только в узлах некоторой сетки xi, т. е. задана таблицей. Если потребовать, чтобы (х;а) совпадала с табличными значениями в n выбранных узлах сетки, то получим систему (1), из которой можно определить параметры ак. Этот способ подбора параметров называется интерполяцией (точнее, лагранжевой интерполяцией). По числу используемых узлов сетки будем называть интерполяцию одноточечной, двухточечной и т. д.

(1)

Если (х;а) нелинейно зависит от параметров, то интерполяцию назовем нелинейной; в этом случае нахождение параметров системы может быть трудной задачей. В данной лабораторной работе мы рассмотрим линейную интерполяцию, когда (х;а) линейно зависит от параметров, т. е. представима в виде так называемого обобщенного многочлена (2).

(2)

Предположим, что задано некоторое упорядоченное множество вещественных абсцисс х1, х2, ..., хn и связанное с ним множество вещественных ординат у1, у2, ..., уn. Пусть х1< х2< ...< хn и каждое уi есть некоторое вещественное число, отвечающее хi, которое определяется математически или в результате каких-либо наблюдений (рисунок 1). Точки (xi,yi) называются узлами интерполяции. Кривая, которая точно проходит через эти узлы, называется интерполяционной кривой.

В данной работе мы будем рассматривать геометрическую интерпретацию интерполяционных полиномов, которая может быть выражена соответствующими симплекс-элементам.

Н

2

иже на рис. 2 изображен одномерный симплекс-элемент, представляющий собой прямолинейный отрезок длины L с двумя узлами, расположенными на концах (по одному на каждом конце).

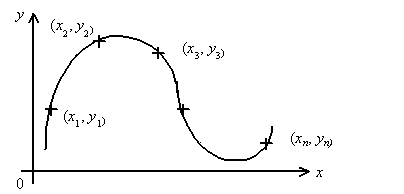
Рис. 1. Интерполяционная кривая f(x,y)

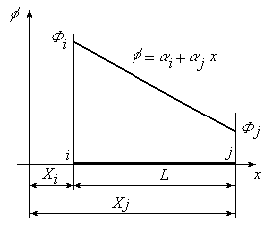
Рис. 2. Одномерный симплекс – элемент

На рис. 3 изображен соответственно двумерный симплекс-элемент, представляющий собой треугольник с прямолинейными сторонами и тремя узлами, по одному в каждой вершине.

Н

3

а рис. 4 изображен трехмерный симплекс-элемент, представляет собой тетраэдр: четыре его узла обозначены индексами i,j,k,l, причем обход узлов i,j,k осуществляется в том порядке, как они записаны, против часовой стрелки, узел l расположен в вершине, находящейся вне плоскости узлов i,j,k.

Рис. 3. Двумерный симплекс – элемент

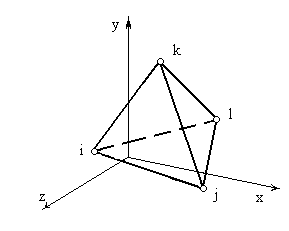
Рис. 4. Трехмерный симплекс – элемент

З

4

адача интерполирования функций симплекс-элементами часто применяется, когда требуется смоделировать на ЭВМ объект (линию, поверхность, объем), описываемый сложной функцией. Проблема заключается в том, что 3D-процессор на видео-плате обычно может работать в пространстве только с плоскостями. Тогда для быстрой прорисовки сложную функцию интерполируют треугольными симплекс-элементами и потом уже выводят на монитор.

Алгоритм нахождения линейного интерполяционного полинома для сиплекс-элемента

В общем (трехмерном) случае линейный интерполяционный полином для симплекс-элемента имеет вид. В двумерном случае z = 0, а в одномерном – z = 0 и y = 0. Определим коэффициенты при переменных и свободный коэффициент с помощью известных значений искомой функции (3) в узловых точках из решения матричного уравнения (4), где С – матрица (6).

(3)

(4)

(5)

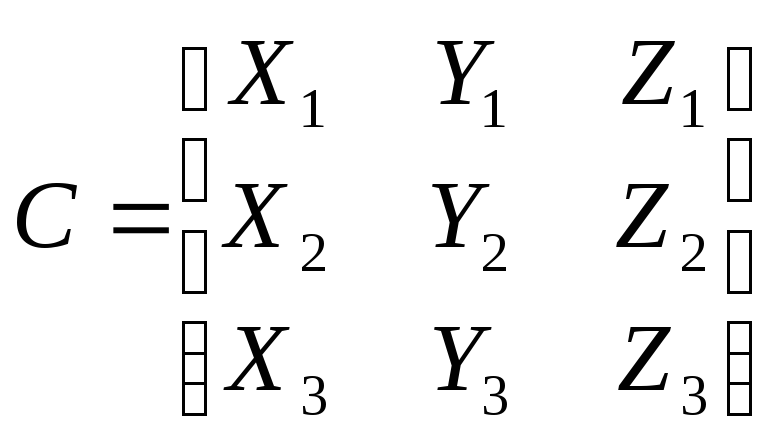(6)

Объединив в матрицу В переменные в интерполяционной формуле, получим матрицу так называемых функций формы (базисных функций) (7).

(7)

(8)

, (9)

5

Тогда интерполяционный полином для искомой функции может быть получен следующей операцией (8). В общем виде полученный интерполяционный полином будет иметь вид (9), где е – индекс, указывающий на отдельный элемент.

Задание

Найти любой линейный интерполяционный полином для одномерного, двумерного и трехмерного симплекс-элемента.

6

Лабораторная работа №2

Линейные интерполяционные полиномы для дискретизованной области в методе конечных элементов

Цель работы: изучить теоретические основы метода конечных элементов, освоить математический аппарат нахождения линейных интерполяционных полиномов для дискретизированной области.

Основы метода конечных элементов

Метод конечных элементов основан на идее аппроксимации непрерывной функции (в физической интерпретации – температуры, давления, перемещения и т.д.) дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей, называемых конечными элементами. Исследуемая геометрическая область разбивается на элементы таким образом, чтобы на каждом из них неизвестная функция аппроксимировалась пробной функцией (как правило, полиномом). Причем эти пробные функции должны удовлетворять граничным условиям непрерывности, совпадающим с граничными условиями, налагаемыми самой задачей. Выбор для каждого элемента аппроксимирующей функции будет определять соответствующий тип элемента.

При построении дискретной модели поступают следующим образом.

В

7

рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками или узлами.

Значения непрерывной величины в каждой узловой точке считается переменной, которая должна быть определена.

Область определения непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области.

Непрерывная величина аппроксимируется на каждом элементе многочленом, который определяется с помощью узловых значений этой величины. Для каждого элемента определяется свой многочлен, но многочлены подбираются таким образом, чтобы сохранилась непрерывность величины вдоль границ элементов. Полином, связанный с каждым элементом, называют функцией элемента.

Объединение конечных элементов в ансамбль. В этом ансамбле узловые значения неизвестной функции должны быть отрегулированы таким образом, чтобы обеспечить наилучшее приближение к истинному непрерывному распределению. Этот этап приводит к алгебраической системе линейных уравнений относительно узловых значений. Эта система и является моделью искомой непрерывной функции.

Решение полученной системы, то есть нахождение узловых значений.

Нахождение значения искомой величины в любой точке области по узловым значениям и функциям элементов.