2.3. Основные задачи гидростатики

Гидростатика в зависимости от частного случая равновесия жидкости позволяет решать следующие четыре типовые задачи:

1) О законе распределения давления. Задача может быть решена интегрированием основного дифференциального уравнения гидростатики (2.10).

2) О форме поверхностей уровня. Эта задача может быть решена двумя способами:

а) аналитически – интегрированием дифференциального уравнения семейства поверхностей уровня (2.12).

б) геометрически – построением, учитывающим, что в каждой данной точке поверхности уровня результирующая массовых сил нормальна к этой поверхности.

3) О механическом взаимодействии покоящейся жидкости с ограничивающими плоскими и криволинейными стенками. Эта задача решается в соответствии с законом распределения давления в жидкости.

4) О механическом взаимодействии покоящейся жидкости с погруженными в неё телами. Эта задача относится к теории плавания и включает в себя теорию остойчивости корабля. (Большой вклад в разработку этой теории внесли академик А.Н. Крылов и адмирал О.В. Макаров.

Четвертая задача относится к внешней задаче гидростатики и поэтому в данном курсе не рассматривается).

2.4. Основное уравнение гидростатики из уравнений Эйлера. Закон распределения давления

Пусть жидкость находится в абсолютном равновесии в поле земного тяготения, т.е. когда на жидкость действует только сила тяжести , а осьнаправлена вверх (рис. 2.7).

Рис. 2.7. Равновесие в поле земного тяготения

Запишем проекции единичных массовых сил на оси координат

, и .

Подставим эти значения в основное уравнение гидростатики .

Следовательно, для этого частного случая равновесия жидкости получим

. (2.13)

Но произведени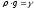е , где- удельный вес жидкости.

Делая подстановку и деля обе части уравнения (2.13) на запишем уравнение в следующем виде

После интегрирования будем иметь

. (2.14)

Или обозначив эту сумму через , получим

(2.15)

Уравнение (2.15) представляет собой основное уравнение гидростатики, полученное путем интегрирования дифференциального уравнения Эйлера. Это и есть закон распределения давления в «абсолютно» покоящейся жидкости: чем меньше координата , т.е. чем глубже погружена та или иная точка, тем больше давление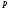в этой точке.

Закон распределения гидростатического давления (2.15) может быть представлено в другой форме. Определим постоянную интегрирования , используя граничные условия для точки, лежащей на свободной поверхности, т.е.и. Подставляя эти значения в (2.14), находим

.

Подставив в уравнение (2.14), получим

,

или . (2.16)

Заменив в уравнении (1.16) , где- глубина расположения точки, найдем

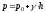, (2.17)

где - абсолютное давление;- давление на свободной поверхности;- избыточное гидростатическое давление в рассматриваемой точке.

Как ясно из формул (2.16) и (2.17), гидростатическое давление линейно зависит от глубины погружения 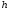: чем больше глубина, тем больше давлениев данной точке.

Этот линейный закон распределения давления может быть изображен графически в виде эпюр абсолютного или избыточного давления (рис.2.8).

а – абсолютного; б - избыточного

Рис. 2.8. Эпюры гидростатического давления