3.5. Живое сечение. Смоченный периметр. Гидравлический радиус

В гидравлических расчётах для характеристики размеров и формы поперечного сечения потока вводят понятие о живом сечении и его элементах: смоченном периметре и гидравлическом радиусе.

Живым сечением называется поверхность в пределах потока, проведённая нормально к линиям тока.

Для круглого трубопровода, когда всё поперечное сечение заполнено жидкостью, живым сечение является площадь круга: (рис.3.6).

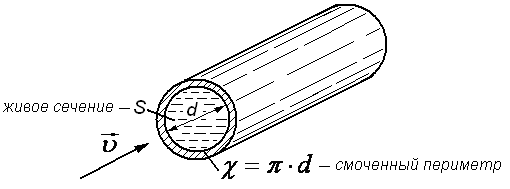
Рис. 3.6. Элементы потока

Смоченным периметром называют ту часть периметра живого сечения, по которой жидкость соприкасается со стенками трубопровода (рис.3.6). Смоченный периметр обычно обозначают греческой 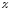(хи). Для круглой трубы полностью заполненной жидкостью смоченный периметр равен длине окружности:

.

Гидравлическим радиусом называют отношение живого сечения к смоченному периметру, т.е. величину

.

Эта величина характеризует удельную, т.е. приходящуюся на единицу длины смоченного периметра, площадь живого сечения. Легко сделать вывод, что поток с наибольшим гидравлическим радиусом при прочих равных условиях имеет минимальную силу трения, приложенную к смоченной поверхности.

Для круглых труб, полностью заполненных жидкостью, гидравлический радиус равен четверти диаметра:

.

Введение гидравлического радиуса как характерного размера позволяет сравнивать по критерию подобия (Re) потоки с разными формами живого сечения.

Рассмотренные основные понятия позволяют решать самые различные практические задачи гидравлики.

Пример 3.1. Определить скорость потока в трубопроводе. Диаметр 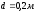, расход воды (несжимаемой жидкости) -.

Решение. Искомая скорость .

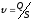Определим площадь живого сечения:

.

Скорость потока:

.

3.6. Уравнение количества движения для потока жидкости

Гидравлика – это техническая механика жидкости, в которой часто используются упрощённые методы для решения инженерных задач. Во многих случаях при решении практических задач гидравлики удобно применять такие центральные понятия механики, как количество движения (уравнение импульсов) и кинетическая энергия.

В связи с этим необходимо рассмотреть возможность вычисления количества движения и кинетическую энергию потока жидкости по средней скорости, а не по действительным местным скоростям. Это позволит существенно упростить гидравлические расчёты.

Для материального тела массой 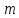, движущегося со скоростью, изменение количества движения за времявследствие действия силывыразится векторным уравнением

, (3.7)

где 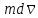- приращение количества движения, обусловленное импульсом.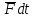

Жидкость представляет собой материальную систему, поэтому основной закон механики может быть приложен к любой выделенной из неё массе.

Применим эту теорему механики к участку потока жидкости с расходом между сечениями 1-1 и 2-2 (выделенный участок заштрихован). Ограничимся рассмотрением только установившегося движения жидкости (рис. 3.7).

За время этот участок переместится в положение, определяемое сечениям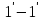ии. Объёмы этих элементов, а, следовательно, и их массыодинаковы, поэтому приращение количества движения будет равно

. (3.8)

Это приращение количества движения обусловлено импульсом всех внешних сил, действующих на объём жидкости между сечениями 1-1 и 2-2. Внешними силами, приложенными к выделенному объёму, являются сила тяжести всего объёма 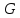, силы давления в первом и втором сечениях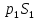и(нормальные к этим сечениям и направленные внутрь объёма), а также реакции стенок трубы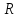, которая складывается из сил давления и трения, распределённых по боковой поверхности объёма.

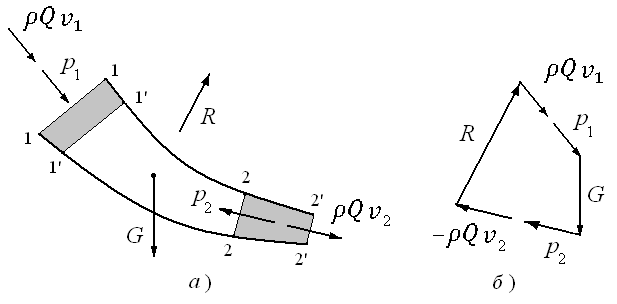
Рис. 3.7. Применение уравнения количества движения

к потоку жидкости

Уравнение импульсов (3.7) для рассматриваемого случая можно записать в виде

.

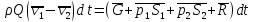После сокращения на

. (3.9)

Составив проекции этого векторного уравнения на три координатные оси, получим три алгебраических уравнения с тремя неизвестными - .

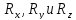Л. Эйлер предложил удобный графический способ нахождения силы . Перенося в формуле (3.?) все слагаемые в одну сторону, можно представить его в виде суммы векторов:

= 0, (3.10)

где вектор взят с обратным знаком (т.е. по направлению обратный действительному). В соответствии с этим выражением (3.10) силу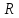можно найти, построив замкнутый многоугольник сил, как это показано на рис. 3.7,а.

Анализ показывает, что при вычислении количества движения и кинетической энергии по средней скорости допускается ошибка, которую можно учесть с помощью двух коэффициентов:

- коэффициента Буссинеска при вычислении количества движения;

- коэффициента Кориолиса 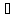в уравнении Бернулли при вычислении кинетической энергии.

Величина обоих коэффициентов зависит от характера распределения скоростей в поперечном сечении потока жидкости. На практике при турбулентном режиме движения коэффициент Кориолиса , а коэффициент Буссинеска. Поэтому обычно полагают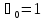. Однако встречаются отдельные случаи, когдадостигает больших значений, и тогда пренебрежение им может привести к значительным погрешностям.

Пример 3.2. Определить силу воздействия потока жидкости на преграду. Пусть жидкость вытекает в атмосферу и наталкивается на безграничную стенку, установленную нормально к потоку. В результате жидкость растекается по стенке, изменяя направление своего течения на 90⁰ (рис. 3.8). Известны площадь сечения потока , скорость истеченияи плотность жидкости.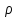

Рис. 3.8. Воздействие струи на преграду

Для решения данной задачи берём фиксированный объём, показанный штриховой линией, и применяем теорему Эйлера. Так как давление внутри струи и по поверхности жидкости равно атмосферному, т.е. избыточное давление равно нулю, уравнение, выражающее теорему Эйлера, для направления, совпадающего с вектором скорости истечения 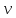, будет иметь вид

,

или . (3.11)

Это и есть сила воздействия потока жидкости на преграду. При другом угле установке стенки или других её форме и размерах в правую формулы (3.11) вводится безразмерный коэффициент, отличный от единицы, но пропорциональность силы 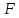произведениюсохранится.