
- •Г.И. Скоморохов
- •Введение
- •Основные физические свойства жидкостей
- •1.1. Определение жидкости
- •1.2. Классификация сил, действующих в жидкости
- •1.3. Основные физические свойства жидкостей
- •Гидростатика
- •2.1. Основные понятия гидростатики
- •2.1.2. Давление абсолютное, избыточное, вакуум
- •2.1.3. Свойства гидростатического давления
- •2.1.4. Основное уравнение гидростатики. Закон Паскаля
- •2.1.5. Поверхности уровня
- •2.2. Дифференциальные уравнения гидростатики
- •2.2.2. Основное дифференциальное уравнение гидростатики
- •2.2.3. Дифференциальное уравнение поверхности
- •2.3. Основные задачи гидростатики
- •2.4. Основное уравнение гидростатики из уравнений Эйлера. Закон распределения давления
- •2.4.1. Геометрическая интерпретация основного уравнения гидростатики
- •2.4.2. Энергетическая интерпретация основного уравнения гидростатики
- •2.5. Применение закона Паскаля в технике
- •2.5.1. Приборы для измерения давления
- •2.5.2. Простейшие гидравлические машины.
- •2.5.1. Приборы для измерения давления
- •2.5.2. Простейшие гидравлические машины. Гидравлический пресс. Мультипликатор
- •2.6. Сила давления на плоскую стенку. Гидравлический парадокс
- •2.7. Центр давления
- •2.8. Сила давления жидкости на криволинейные стенки
- •2.9. Закон Архимеда
- •2.10. Относительное равновесие жидкости
- •2.10.1. Движение сосуда с жидкостью прямолинейно в произвольном направлении с постоянным ускорением
- •2.10.2. Движение сосуда с жидкостью вертикально вниз с постоянным ускорением
- •2.10.3. Равномерное вращение цилиндрического сосуда с жидкостью вокруг вертикальной оси
- •2.10.4. Равновесие жидкости в поле центробежных сил при нулевой или слабой гравитация
- •2.11. Формы поверхностей раздела между жидкостью и газом (паром) в условиях динамической невесомости
- •3. Гидродинамика
- •3.2. Виды движения жидкости
- •3.3. Линия тока и траектория частицы, элементарная струйка
- •3.4. Закон сохранения массы. Расход. Уравнение неразрывности
- •3.5. Живое сечение. Смоченный периметр. Гидравлический радиус
- •3.6. Уравнение количества движения для потока жидкости
- •3.7. Дифференциальные уравнения движения идеальной жидкости в форме уравнений Эйлера
- •3.8. Основное дифференциальное уравнение установившегося движения идеальной жидкости
- •3.9. Уравнение Бернулли для струйки идеальной несжимаемой жидкости
- •3.9.1. Геометрический смысл уравнения Бернулли.
- •3.9.2. Энергетический смысл уравнения Бернулли
- •3.9.1. Геометрический смысл уравнения Бернулли. Трубка Пито
- •3.9.2. Энергетический смысл уравнения Бернулли
- •3.10. Уравнение Бернулли для элементарной струйки вязкой жидкости
- •3.11. Уравнение Бернулли для потока вязкой несжимаемой жидкости
- •3.12. Классификация гидравлических потерь. Гидравлический и пьезометрический уклоны
- •3.13. Применение уравнения Бернулли в технике
- •3.14. Основы гидродинамического подобия
- •3.15. Режимы течения жидкости
- •3.16. Критерий Рейнольдса и гидравлический радиус
- •4. Ламинарное течение жидкости
- •4.2. Расход при ламинарном режиме в круглой трубе. Формула Пуазейля. Коэффициент Кориолиса
- •4.3. Потери на трение. Формула Дарси-Вейсбаха
- •4.4. Влияние теплообмена на профиль скоростей и потери по длине
- •4.5. Начальный участок ламинарного потока
- •4.6. Потери на трение при ламинарном течении в каналах некруглой формы
- •4.7. Ламинарное течение в зазорах
- •4.7.1. Течение через зазор между параллельными стенками под действием умеренного перепада давлений
- •4.7.2. Течение через зазор при больших перепадах давления
- •5. Турбулентное движение жидкости
- •5.1. Пульсация местной скорости в турбулентном потоке
- •5.2. Распределение осреднённых местных скоростей в турбулентном потоке
- •5.3. Гидравлически гладкие и шероховатые трубы
- •5.4. Потери по длине в гидравлически гладких трубах
- •5.6. Влияние шероховатости на потери. График Никурадзе
- •Заключение
- •Библиографический список
- •Оглавление
2.1.2. Давление абсолютное, избыточное, вакуум
Числовое значение давления определяется не только принятой системой единиц, но и выбранным началом отсчета. Исторически сложились три системы отсчета давления: абсолютная, избыточная и вакуумметрическая (рис.2.2).
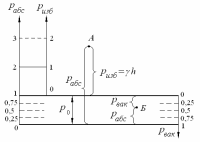
Рис. 2.2. Шкалы давления. Связь между давлением
абсолютным, избыточным и вакуумом
Абсолютное
давление
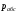 отсчитывается от абсолютного нуля (рис.
2.2). В этой системе атмосферное давление
отсчитывается от абсолютного нуля (рис.
2.2). В этой системе атмосферное давление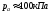 .
Следовательно, абсолютное давление
равно
.
Следовательно, абсолютное давление
равно
 .
.
Абсолютное давление всегда является величиной положительной.
Избыточное
давление
 отсчитывается от атмосферного давления,
т.е. от условного нуля. Чтобы перейти от
абсолютного к избыточному давлению
необходимо вычесть из абсолютного
давления атмосферное, которое в
приближенных расчетах можно принять
равным 1ат:
отсчитывается от атмосферного давления,
т.е. от условного нуля. Чтобы перейти от
абсолютного к избыточному давлению
необходимо вычесть из абсолютного
давления атмосферное, которое в
приближенных расчетах можно принять
равным 1ат:
 .
.
Иногда избыточное давление называют манометрическим.
Вакуумметрическим
давлением или вакуумом
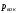 называется недостаток давления до
атмосферного
называется недостаток давления до
атмосферного
 .
.
Избыточное давление показывает либо избыток над атмосферным, либо недостаток до атмосферного. Ясно, что вакуум может быть представлен как отрицательное избыточное давление
 .
.
Как видно, эти три шкалы давления различаются между собой либо началом, либо направлением отсчета, хотя сам отсчет может вестись при этом в одной и той же системе единиц. Если давление определяется в технических атмосферах, то к обозначению единицы давления (ат) приписывается ещё одна буква, в зависимости от того, какое давление принято за «нулевое» и в каком направлении ведется положительный отсчет.
Например:
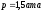 -
абсолютное давление равно 1,5 кг/см2;
-
абсолютное давление равно 1,5 кг/см2;
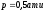 -
избыточное давление равно 0,5 кг/см2;
-
избыточное давление равно 0,5 кг/см2;
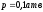 -
вакуум составляет 0,1 кг/см2.
-
вакуум составляет 0,1 кг/см2.
Чаще всего инженера интересует не абсолютное давление, а его отличие от атмосферного, поскольку стенки конструкций (бака, трубопровода и т.п.) обычно испытывают действие разности этих давлений. Поэтому в большинстве случаев приборы для измерения давления (манометры, вакуумметры) показывают непосредственно избыточное (манометрическое) давление или вакуум.
Единицы давления. Как следует из самого определения давления, его размерность совпадает с размерностью напряжения, т.е. представляет собой размерность силы, отнесенную к размерности площади.
За
единицу давления в Международной системе
единиц (СИ) принят паскаль
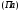 — давление, вызываемое силой
— давление, вызываемое силой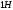 ,
равномерно распределенной по нормальной
к ней поверхности площадью
,
равномерно распределенной по нормальной
к ней поверхности площадью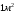 ,
т.е.
,
т.е.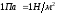 .
Наряду с этой единицей давления применяют
укрупненные единицы: килопаскаль (кПа)
и мегапаскаль (МПа):
.
Наряду с этой единицей давления применяют
укрупненные единицы: килопаскаль (кПа)
и мегапаскаль (МПа):
 ;
;  ;
; .
.
В технике в настоящее время в некоторых случаях продолжают применять также техническую МКГСС (метр, килограмм-сила, секунда, а) и физическую СГС (сантиметр, грамм, секунда) системы единиц. Используются также внесистемные единицы — техническую атмосферу и бар:
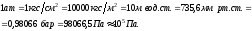 Не
следует также смешивать техническую
атмосферу
Не
следует также смешивать техническую
атмосферу
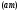 с физической
с физической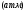 ,
которая все ещё имеет некоторое
распространение в качестве единицы
давления:
,
которая все ещё имеет некоторое
распространение в качестве единицы
давления:
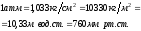
2.1.3. Свойства гидростатического давления
Гидростатическое давление обладает двумя основными свойствами.
1-ое свойство. Силы гидростатического давления в покоящейся жидкости всегда направлены внутрь по нормали к площадке действия, т.е. являются сжимающими.
Это свойство доказывается от противного. Если предположить, что силы направлены по нормали наружу, то это равносильно появлению в жидкости растягивающих напряжений, которых она воспринимать не может (это вытекает из свойств жидкости).
2-ое свойство. Величина гидростатического давления в любой точке жидкости по всем направлениям одинаково, т.е. не зависит от ориентации в пространстве площадки, на которую оно действует
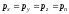 ,
,
где
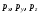 - гидростатические давления по направлению
координатных осей;
- гидростатические давления по направлению
координатных осей;
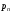 -
то же по произвольному направлению
-
то же по произвольному направлению
 .
.
Для
доказательства этого свойства выделим
в неподвижной жидкости элементарный
объем в форме тетраэдра с ребрами,
параллельными координатным осям и
соответственно равными
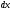 ,
,
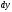 и
и
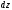 (рис.
2.3).
(рис.
2.3).
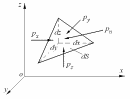
Рис. 2.3. Схема для доказательства свойства
о независимости гидростатического давления от направления
Введем
обозначения:
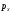 -
гидростатическое
давление, действующее на грань, нормальную
к оси
-
гидростатическое
давление, действующее на грань, нормальную
к оси
 ;
;
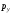 -
давление на грань, нормальную к оси
-
давление на грань, нормальную к оси
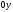 ;
;
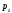 -
давление на грань, нормальную к оси
-
давление на грань, нормальную к оси
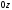 ;
;
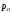 -
давление, действующее на наклонную
грань;
-
давление, действующее на наклонную
грань;
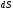 -
площадь этой грани;
-
площадь этой грани;
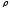 -
плотность жидкости.
-
плотность жидкости.
Запишем условия равновесия для тетраэдра (как для твердого тела) в виде трех уравнений проекций сил и трех уравнений моментов:
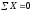 ,
, 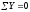 ,
, ;
;
 ,
,  ,
, .
.
При уменьшении в пределе объема тетраэдра до нуля система действующих сил преобразуется в систему сил проходящих через одну точку, и, таким образом, уравнения моментов теряют смысл.
Таким
образом, внутри выделенного объема на
жидкость действует единичная массовая
сила, проекции ускорений которой равны
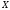 ,
,
 ,
и
,
и
 .
В гидравлике принято массовые силы
относить к единице массы, а так как
.
В гидравлике принято массовые силы
относить к единице массы, а так как
 ,
то проекция единичной массовой силы
численно будет равна ускорению.
,
то проекция единичной массовой силы
численно будет равна ускорению.
 ;
;  ;
; ,
,
где
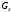 ,
,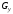 ,
, - проекции единичной массовой силы на
оси координат;
- проекции единичной массовой силы на
оси координат;
 -
масса жидкости;
-
масса жидкости;
 -
ускорение.
-
ускорение.
Составим
уравнение равновесия выделенного объема
жидкости в направлении оси
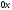 ,
учитывая
при этом, что все силы направлены по
нормалям к соответствующим площадкам
внутрь объема жидкости:
,
учитывая
при этом, что все силы направлены по
нормалям к соответствующим площадкам
внутрь объема жидкости:
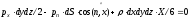 ,
(2.4)
,
(2.4)
где
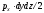 - проекция силы от гидростатического
давления
- проекция силы от гидростатического
давления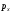 ;
;
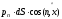 -
проекция силы от давления
-
проекция силы от давления
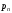 ;
;
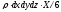 -
проекция массовой силы, действующей на
тетраэдр.
-
проекция массовой силы, действующей на
тетраэдр.
Разделив
уравнение (2.2) на площадь
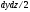 ,
которая
равна площади проекции наклонной
грани
,
которая
равна площади проекции наклонной
грани
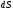 на
плоскость
на
плоскость
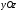 ,
т.
е.
,
т.
е.
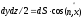 ,
получим
,
получим
 .
.
При
стремлении размеров тетраэдра к нулю
последний член уравнения, содержащий
множитель
 ,
также
стремится к нулю
,
также
стремится к нулю
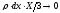 ,
а давления
,
а давления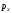 и
и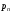 остаются
величинами конечными.
остаются
величинами конечными.
Следовательно, в пределе получим
 или
или
 .
.
Аналогично
составляя уравнения равновесия вдоль
осей
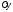 и
и
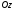 ,
находим
,
находим
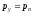 ,
,  ,
,
или
 .
.
Так
как размеры тетраэдра
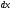 ,
,
 и
и
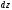 и
наклон площадки
и
наклон площадки
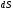 взяты
произвольно, то, следовательно, в пределе
при стягивании тетраэдра в точку давление
в этой точке по всем направлениям будет
одинаково. Что и требовалось доказать.
взяты
произвольно, то, следовательно, в пределе
при стягивании тетраэдра в точку давление
в этой точке по всем направлениям будет
одинаково. Что и требовалось доказать.
Рассмотренное свойство давления в неподвижной жидкости имеет место также при движении невязкой (идеальной) жидкости. При движении же реальной жидкости возникают касательные напряжения, вследствие чего давление в реальной жидкости указанным свойством, строго говоря, не обладает.
В
общем случае
давление
в точке зависит от координат рассматриваемой
точки, а при неустановившемся движении
жидкости может изменяться в каждой
данной точке с течением времени:  .
.
