4.7.2. Течение через зазор при больших перепадах давления

Положение существенно меняется, если перепад давления настолько велик, что вязкость жидкости на входе в зазор оказывается значительно большей, чем на выходе. Как отмечалось во введении, с уменьшением давления вязкость жидкости уменьшается.

В данном случае в том же направлении действует и градиент температур: трение приводит к тому, что по мере продвижения вглубь зазора жидкость нагревается, и вязкость ее из-за этого падает еще больше. Этот эффект особенно значителен при большой толщине стенок, затрудняющей отвод тепла из зазора.

Падение вязкости приводит к тому, что гидравлический уклон по глубине зазора не остается постоянным, как было бы при малой разности давлений и изотермическом течении, а постепенно уменьшается. В результате линии полных напоров и пьезометрических высот приобретают форму кривых, обращенных вогнутостью кверху.

5. Турбулентное движение жидкости

5.1. Пульсация местной скорости в турбулентном потоке

Сложность кинематической структуры турбулентного по­тока затрудняет применение обычных методов математического анализа для его описания. Поэтому в отличие от раз­дела о ламинарном течении жидкости, содержавшего строгие выводы всех положений, в настоящем разделе будут приводиться в основном чисто физические обоснования за­кономерностей турбулентного режима, описываемых полуэмпирическими формулами.

Приступая к анализу особенностей турбулентного движе­ния, мы прежде всего сталкиваемся с явлением пульсации местной скорости в любой точке потока. Действительно, че­рез произвольно выбранную точку А турбулентного потока с координатами (в осях, связанных с границами потока, например, со стенкой трубопровода) непрерывно проходят разные частицы жидкости, перемещающиеся по разным траекториям и обладающие в момент прохождения через эту точку разными по величине и направлению скоростями. В результате местная скорость в точке А непрерывно изменяется, причем изменения эти носят характер пульсации, т.е. непериодических колебаний около некоторого осреднённого значения. Если местную скорость измерять прибором, обладающим большой инерционностью (например, трубка Пито), то можно пульсацию и не обнаружить. Однако использование практически безинерционного измерителя скорости (например, термоэлектрического анемометра) выявляет картину, представленную на рис.5.1. Здесь - осредненная во времени местная скорость (она совпадает с осредненным значением составляющей 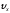, так как средние значения составляющихиравны нулю, поскольку через стенку жидкость протекать не может);- мгновенная пульсационная скорость в направлении оси в данный момент времени; 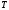- время осреднения.

Рис.5.1. Пульсация местной скорости

Нетрудно заметить, что осредненная скорость может быть определена формулой

. (5.1)

Если ламинарный режим - понятие вполне однозначное (бессмысленно говорить о большей или меньшей ламинарности потока), то один турбулентный поток может отличаться от другого степенью турбулентности. Действительно, при одной и той же осредненной скорости среднее отклонение от нее, характеризующее интенсивность пульсации, может у разных потоков оказаться различным.

Под степенью турбулентности, представляющей собой своего рода критерий кинематического подобия турбулентных потоков, принято понимать отношение средней квадратичной пульсационной скорости за время Т к осредненной скорости в той же точке за тот же промежуток времени:

. (5.2)

Турбулентный поток можно условно рассматривать как результат наложения двух потоков: пульсационного и осреднённого. Умножая и деля правую часть выражения (5.2) на , замечаем, что степень турбулентности есть не что иное, как корень квадратный из отношения кинетических энергий этих потоков. Сравним «поведение» местных скоростей ламинарного и турбулентного потоков при постоянном и переменном расходе жидкости (рис.5.2).

Рис.5.2. Сравнение ламинарного и турбулентного течений

с позиций стационарности потока

Пусть расход в трубопроводе регулируется вентилем. Убедившись в том, что достигнутый расход соответствует ламинарному режиму (), оставим вентиль в постоянном положении. Измеряя местную скорость в любой точке потока на протяжении некоторого промежутка времени, убедимся в том, что она, как и сам расход (а с ним и средняя скорость потока), будет оставаться постоянной. Такое течение, как известно, называется установившимся, или стационарным.

При другом постоянном положении вентиля, соответствующем турбулентному течению жидкости, инерционный измеритель будет, как и при ламинарном режиме, регистрировать в любой точке потока постоянное значение местной скорости. Однако в действительности мгновенная местная скорость будет при этом непрерывно изменяться, пульсируя около этого осредненного значения. Такое турбулентное течение может быть названо квазистационарным (частица «квази» в переводе с латинского означает «как бы»).

Теперь представим себе, что измерение местной скорости производится в условиях переменного расхода.

Если, убедившись в том, что данное постоянное положение вентиля обеспечивает ламинарный режим, мы начнем, например, вентиль закрывать, то при этом режим течения не перестанет быть ламинарным (уменьшается), но местная скорость в любой точкеА будет изменяться соответственно общему уменьшению расхода и средней скорости. Течение окажется неустановившимся (нестационарным).

При турбулентном режиме течения изменение расхода будет означать и изменение осредненной скорости, причем пульсация местных скоростей будет происходить около этой переменной величины. Таков общий случай турбулентного течения.

Таким образом, ламинарное течение может быть как установившимся, так и неустановившимся. Турбулентное же течение всегда представляет собой течение неустановившееся, но и здесь полезно выделить особый случай, характеризующийся постоянством осредненных местных скоростей. Такое квазистадионарное турбулентное течение подчиняется многим законам установившегося движения жидкости. Так для него остается справедливым уравнение Бернулли в той форме, в какой оно применяется для установившегося потока вязкой жидкости.