4.5. Начальный участок ламинарного потока

Формирование параболического профиля скоростей происходит не сразу, а постепенно, на протяжении так называемого начального участка потока, примыкающего к входному сечению трубы. Почти равномерное распределение скоростей на входе в трубу под действием трения становится мере по продвижения жидкости вперед все менее равномерно, пока в конце начального участка не подчинится закону квадратной параболы. При этом коэффициент неравномерности распределения кинетической энергии в сечении потока постепенно возрастает от 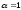на входе в трубув конце начального участка. Дальше, на всём остальном протяжении потока, сохраняется характерный для стабилизированного ламинарного течения параболический профиль скоростей ().

Существуют разные теории начального участка, различающиеся между собой наперед принятыми гипотезами. Авторы одних теорий строят модель начального участка исходя из того, что в конечном его сечении профиль скоростей переходит в параболический. Авторы других теорий исходят из предположения, что пограничный слой, толщина которого постепенно растет, смыкается в конце начального участка, заполняя все живое сечение потока. Естественно, что первое предположение хорошо подтверждается опытом вблизи конечного сечения этого участка, а второе - вблизи входного.

По Буссинеску относительная длина начального участка составляет

, (4.18)

по Л.Шиллеру

. (4.19)

Результаты Шиллера ближе других к опытным данным. Легко подсчитать по его формуле, что максимально возможная длина начального участка, достигаемая при , составляет 66 калибров.

Чем более равномерно в том или ином сечении начального участка распределяются местные скорости, тем резче переход от нулевой скорости потока на его границе к постоянной конечной скорости в так называемом потенциаль­ном ядре. Таким образом, на начальном участке потока, особенно у самого входа в трубу, абсолютная величина радиального градиента скорости у стенки больше, чем при стабилизированном профиле скоростей. Это приводит к увеличению напряжения трения на границе потока, а следовательно, к увеличению гидравлических потерь. У коротких трубопроводов, длина которых соизмерима с величиной начального участка, потери нельзя определять просто по формуле Пуазейля или по формуле Дарси с коэффициентом трения. Необходимо при их расчете вводить поправку на влияние начального участка,

Это влияние может быть оценено поправочным коэффициентом, представляющим собой убывающую функцию относи­тельной абсциссы сечения начального участка:

; (4.20)

. (4.21)

где 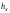- потери на отрезке начального участка длиной .

При коэффициентт.е. напор, потерянный на первой половине начального участка, на 25% превышает потери на такой же длине в области стаби­лизированного потока. Для всего начального участка () этот коэффициент равен уже всего 1,09. При потери на трение по длине составляют

. (4.22)

Учитывая (4.27), получим окончательно

. (4.23)

Из этой формулы видно, что постоянную поправку 0,165 следует вводить лишь при достаточно малых значениях второго слагаемого, соизмеримых с самой поправкой.