4.2. Расход при ламинарном режиме в круглой трубе. Формула Пуазейля. Коэффициент Кориолиса 

При выводе теоретической формулы для определения расхода жидкости воспользуемся полученным законом распределения скоростей по сечению (закон Стокса).

Выдели в потоке элементарное сечение в виде кольца, радиус которого - , ширина -, а площадь -(рис. 4.2).

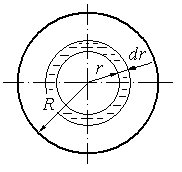
Рис. 4.2. К выводу формулы Пуазейля

Определим расход жидкости через это бесконечно малое сечение

.

Интегрируя, получаем объёмный расход через всё живое сечение потока:

;

Расход жидкости через живое сечение потока можно выразить и через диаметр трубы, тогда получим

- формула Пуазейля. (4.8)

Этот закон впервые был сформулирован Г. Хагеном в 1839 году и вскоре повторно выведен французским врачом Жаном Пуазейлем (1799-1869) в 1840 году. Согласно закону, секундный объёмный расход жидкости пропорционален перепаду давления на единицу длины трубки и четвёртой степени диаметра трубы. Эта зависимость была получена чисто эмпирическим путём при исследовании движения жидкости в тонких капиллярных трубках.

Среднюю скорость по сечению найдём делением расхода на площадь живого сечения потока

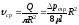. (4.9)

Сравнив выражение для средней скорости (4.9) с выражением для максимальной скорости (4.6) получим, что

.

т.е. при ламинарном режиме течения средняя скорость в два раза меньше максимальной.

Определим коэффициент неравномерности расхода как отношение кинетической энергии, вычисленной по местным скоростям, к энергии, вычисленной по средней скорости потока

.

После интегрирования, подстановки пределов и сокращения получим значение коэффициента Кориолиса для ламинарного течения жидкости в круглой трубе

.

Таким образом, кинетическая энергия ламинарного потока в 2 раза больше кинетической энергии, рассчитанной по средней скорости.

4.3. Потери на трение. Формула Дарси-Вейсбаха

Определим потери напора на трение при ламинарном течении жидкости в круглой трубе. Применим к двум сечениям 1-1 и 2-2 (рис.4.3) уравнение Бернулли:

.

Для нашего случая

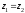- т.к. труба горизонтальная;

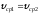- сечение потока постоянно;

- течение ламинарное.

В результате уравнение Бернулли упростится:

.

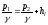Откуда . (4.10)

Из формулы Пуазейля (4.20) выразими подставим в (4.10 22)

; (4.11)

Учитывая, что и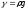, получим окончательно

. (4.12)

Выразив в формуле (4.12 24) расход через среднюю скорость , получим

. (4.13)

Таким образом, при ламинарном течении потери на трение линейно зависят от расхода или средней скорости потока. Характерна для ламинарного режима и прямая зависимость потерь от вязкости.

В такой форме следует учитывать потери по длине в уравнении Бернулли, т.е.

.

Для того чтобы формулу Пуазейля структурно привести к форме Дарси-Вейсбаха, достаточно умножить и разделить правую часть формулы (4.13) на

.

Подставляя , получаем

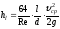. (4.14)

Сравнивая (4.14) и формулу Дарси-Вейсбаха (3.28), приходим к выводу, что при ламинарном течении в круглой цилиндрической трубе

. (4.15)

Графически эта зависимость представлена на рис. 4.3.

Рис. 4.3. Зависимость - опытные точки лежат

выше теоретической кривой