2. Гидростатика

2.1. Основные понятия гидростатики

2.2. Дифференцальные уравнения гидростатики

2.3. Основные задачи гидростатики

2.4. Основное уравнение гидростатики из уравнений

Эйлера. Закон распределения давления

2.5. Применение закона Паскаля в технике

2.6. Сила давления на плоскую стенку. Гидравлический

парадокс

2.7. Центр давления

2.8. Сила давления жидкости на криволинейные стенки

2.9. Закон Архимеда

2.10. Относительное равновесие жидкости в движущихся

сосудах

2.11. Формы поверхностей раздела между жидкостью и

газом (паром) в условиях динамической невесомости

Целью настоящей главы является определение характера напряжений, возникающих в покоящейся жидкости, и выявление законов их изменения. Содержание данной главы позволяет инженерам овладеть методами расчета элементов различных агрегатов жидкостных ракетных двигателей, находящихся под силовым воздействием покоящейся жидкости. Рассмотрены также вопросы, касающиеся относительного равновесия жидкости в движущихся сосудах, а также определения формы поверхностей раздела между жидкостью и газом (паром) в условиях динамической невесомости.

В ракетно-космической технике масса баков с жидким топливом составляет около 85% общей массы летательных аппаратах, что и обуславливает наличие целого ряда задач по разделу гидростатика.

2.1. Основные понятия гидростатики

2.1.1. Равновесие жидкости. Гидростатическое давление

2.1.2. Давление абсолютное, избыточное, вакуум

2.1.3. Свойства гидростатического давления

2.1.4. Основное уравнение гидростатики. Закон Паскаля

2.1.5. Поверхности уровня

2.1.1. Равновесие жидкости. Гидростатическое давление

Гидростатика - раздел гидравлики о законах равновесия жидкости и её взаимодействии с твердыми телами и газами.

Равновесие капельных жидкостей. Под равновесием жидкости понимается отсутствие перемещения одних её частей относительно других и жидкости в целом относительно ограничивающих её стенок. При этом сам сосуд вместе с заключенной в нем жидкостью может перемещаться в любом направлении и с любым ускорением. Различают «абсолютное» и относительное равновесие (покой) жидкости.

«Абсолютное» равновесие» - это равновесие жидкости в неподвижном относительно земли сосуде в поле только гравитационных сил. При «абсолютном» равновесии результирующая массовых сил направлена вертикально вниз.

Относительное равновесие жидкости - это равновесие её в поле силы тяжести и сил инерции. При относительном равновесии результирующая массовых сил может быть направлена в любом направлении.

Очевидно, что «абсолютное» равновесие представляет собой частный случай относительного, характеризующийся тем, что из всех массовых сип действует только сила тяжести.

В жидкости, находящейся в покое, силы трения, обусловленные вязкостью, не проявляются (не действуют касательные силы). Поэтому, реальные жидкости по своим свойствам будут очень близки к идеальным, и, следовательно, все задачи гидростатики будут решаться с большой точностью.

Гидростатическое давление. Как отмечалось ранее, на жидкость могут действовать поверхностные и массовые силы. Массовые силы в соответствии со вторым законом Ньютона про­порциональны массе жидкости или, для однородной жидкости, - ее объёму. К ним относятся сила тяжести и сила инерции переносного движения системы, действующая на жидкость при относительном ее покое (а также при ускоренном движении).

Поверхностные силы непрерывно распределены по поверхности жидкости и при равномерном их распределении пропорциональны площади этой поверхности. Эти силы обусловлены непосредственным воздействием соседних объемов жидкости на данный объем или же воздействием других тел (твердых или газообразных), соприкасающихся с данной жидкостью. Как следует из третьего закона Ньютона, с такими же силами, но в противоположном направлении, жидкость действует на соседние с нею тела.

Согласно положению теоретической механики любая система, в том числе и жидкостная, может находиться в равновесии только при условии равенства нулю равнодействующей всех приложенных к ней внешних сил, а также их результирующего момента. Состояние жидкости при этом характеризуется только внутренними (молекулярными) силами.

Рассечём жидкость воображаемой поверхностью и выделим около точки 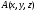с координатами некоторую площадку величиной(рис. 2.1).

Рис. 2.1. Разложение поверхностной силы на две составляющие

В общем случае поверхностная сила , действующая в точкена площадке, направлена под некоторым углом к ней, и ее можно разложить на две силы:- нормальную сжимающую силу; и 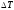- тангенциальную силу или силу трения. Нормальная сжимающая сила может быть условно представлена в виде вектора, который направлен по внутренней нормали к выделенной площадке (т.е. внутрь объёма жидкости) и приложена к площадке в точке.

Среднее напряжение этой силы можно найти, отнеся её к площади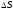по формуле

. (2.1)

Для определения истинного значения напряжения в точке 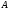необходимо перейти к пределу этого отношения при условии, что площадка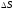уменьшении до нуля

. (2.2)

Нормальное напряжение силы давления, называется гидромеханическим давлением, или просто давлением, и обозначается буквой .

На внешней поверхности силы давления всегда направлены по нормали внутрь объема жидкости и, следовательно, являются сжимающими. Таким образом, в неподвижной жидкости возможен лишь один вид напряжения - напряжение сжатия, т.е. гидростатическое давление.

Касательное напряжение в жидкости, т. е. напряжение трения, обозначается буквой и выражается подобно давлению пределом отношения, а размерность его та же, что и давления,

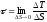. (2.3)