3.16. Критерий Рейнольдса и гидравлический радиус

Числовые значения коэффициента трения 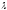и коэффициента местного сопротивлениязависят от режима течения и определяются в соответствии с законами гидродинамического подобия.

Для того чтобы потоки вязкой жидкости были между собой динамически подобны, необходимо кроме пропорциональности сходственных размеров и равенства соответствующих углов соблюдать равенство отношений инерционных сил к силам внутреннего трения, обусловленным вязкостью. Можно доказать (см. п. 3.15), что это условие означает равенство отношения

. (3.50)

Здесь индексами 1 и 2 обозначены величины, относящиеся к каждому из двух сравниваемых потоков, причём под 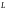понимается любой характерный для потока размер. Возможность произвольного выбора линейного размера вытекает из условия геометрического подобия потоков, означающего пропорциональность сходственных размеров

.

Условие (3.504.2) может быть записано и как критерий подобия Рейнольдса

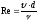. (3.51).

Для достижения динамического подобия потоков требуется соблюдение равенства чисел Рейнольдса

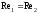или .

Число Рейнольдса представляет собой меру отношения инерционных сил к силам внутреннего трения. Это критерий, учитывающий влияние вязкости на подобие.

При рассмотрении потока жидкости в круглой трубе в качестве характерного размера при определении числа Рейнольдса принимается внутренний диаметр трубы, а за скорость – средняя скорость потока (рис. 3.19,е)

. (3.52)

Для потока некруглого сечения при вычислении Re удобно в качестве характерного размера принимать так называемый гидравлический радиус

. (3.53)

Гидравлическим радиусом называется отношение площади живого сечения к смоченному периметру(каппа)

. (3.54)

При прочих равных условиях (одинаковой скорости, одинаковой вязкости) совпадение гидравлических радиусов означает равенство отношений инерционных сил к силам внутреннего трения (поскольку инерционные силы зависят от площади сечения, а поверхность трения - от величины смоченного периметра).

Введение гидравлического радиуса как характерного размера при определении числа Рейнольдса позволяет сравнивать по критерию потоки с разными формами живого сечения (рис. 3.19).

Рис.3.19. К определению гидравлического радиуса

при напорном течении

При напорном течении жидкости в прямоугольном канале (рис.3.19,а) гидравлический радиус

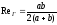. (3.55)

Для зазора (рис. 3.19,б), образованного параллельными стенками, когда, получим, пренебрегая слагаемымв знаменателе правой части формулы (3.55)

. (3.56)

По этой же формуле определяется гидравлический радиус в случае кольцевого зазора, если (рис. 3.19,в).

При напорном течении в канале квадратного сечения (рис. 3.19,г)

. (3.57)

В случае эллиптического сечения (рис. 3.19,д)

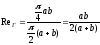. (3.58)

При напорном течении в круглой трубе (рис. 3.19,е)

. (3.59)

Таким образом, гидравлический радиус круглого сечения не совпадает с геометрическим - он не в два, а в четыре раза меньше геометрического диаметра. Следовательно, при переходе от числа Рейнольдса по гидравлическому радиусу к числу Рейнольдса по диаметру необходимо помнить, что

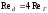. (3.60)

Следует также иметь в виду, что совпадение чисел Рейнольдса по гидравлическому радиусу у потоков с различными формами сечения не гарантирует в полной мере динамического подобия, так как в этом случае отсутствует подобие геометрическое.