
- •Г.И. Скоморохов
- •Введение
- •Основные физические свойства жидкостей
- •1.1. Определение жидкости
- •1.2. Классификация сил, действующих в жидкости
- •1.3. Основные физические свойства жидкостей
- •Гидростатика
- •2.1. Основные понятия гидростатики
- •2.1.2. Давление абсолютное, избыточное, вакуум
- •2.1.3. Свойства гидростатического давления
- •2.1.4. Основное уравнение гидростатики. Закон Паскаля
- •2.1.5. Поверхности уровня
- •2.2. Дифференциальные уравнения гидростатики
- •2.2.2. Основное дифференциальное уравнение гидростатики
- •2.2.3. Дифференциальное уравнение поверхности
- •2.3. Основные задачи гидростатики
- •2.4. Основное уравнение гидростатики из уравнений Эйлера. Закон распределения давления
- •2.4.1. Геометрическая интерпретация основного уравнения гидростатики
- •2.4.2. Энергетическая интерпретация основного уравнения гидростатики
- •2.5. Применение закона Паскаля в технике
- •2.5.1. Приборы для измерения давления
- •2.5.2. Простейшие гидравлические машины.
- •2.5.1. Приборы для измерения давления
- •2.5.2. Простейшие гидравлические машины. Гидравлический пресс. Мультипликатор
- •2.6. Сила давления на плоскую стенку. Гидравлический парадокс
- •2.7. Центр давления
- •2.8. Сила давления жидкости на криволинейные стенки
- •2.9. Закон Архимеда
- •2.10. Относительное равновесие жидкости
- •2.10.1. Движение сосуда с жидкостью прямолинейно в произвольном направлении с постоянным ускорением
- •2.10.2. Движение сосуда с жидкостью вертикально вниз с постоянным ускорением
- •2.10.3. Равномерное вращение цилиндрического сосуда с жидкостью вокруг вертикальной оси
- •2.10.4. Равновесие жидкости в поле центробежных сил при нулевой или слабой гравитация
- •2.11. Формы поверхностей раздела между жидкостью и газом (паром) в условиях динамической невесомости
- •3. Гидродинамика
- •3.2. Виды движения жидкости
- •3.3. Линия тока и траектория частицы, элементарная струйка
- •3.4. Закон сохранения массы. Расход. Уравнение неразрывности
- •3.5. Живое сечение. Смоченный периметр. Гидравлический радиус
- •3.6. Уравнение количества движения для потока жидкости
- •3.7. Дифференциальные уравнения движения идеальной жидкости в форме уравнений Эйлера
- •3.8. Основное дифференциальное уравнение установившегося движения идеальной жидкости
- •3.9. Уравнение Бернулли для струйки идеальной несжимаемой жидкости
- •3.9.1. Геометрический смысл уравнения Бернулли.
- •3.9.2. Энергетический смысл уравнения Бернулли
- •3.9.1. Геометрический смысл уравнения Бернулли. Трубка Пито
- •3.9.2. Энергетический смысл уравнения Бернулли
- •3.10. Уравнение Бернулли для элементарной струйки вязкой жидкости
- •3.11. Уравнение Бернулли для потока вязкой несжимаемой жидкости
- •3.12. Классификация гидравлических потерь. Гидравлический и пьезометрический уклоны
- •3.13. Применение уравнения Бернулли в технике
- •3.14. Основы гидродинамического подобия
- •3.15. Режимы течения жидкости
- •3.16. Критерий Рейнольдса и гидравлический радиус
- •4. Ламинарное течение жидкости
- •4.2. Расход при ламинарном режиме в круглой трубе. Формула Пуазейля. Коэффициент Кориолиса
- •4.3. Потери на трение. Формула Дарси-Вейсбаха
- •4.4. Влияние теплообмена на профиль скоростей и потери по длине
- •4.5. Начальный участок ламинарного потока
- •4.6. Потери на трение при ламинарном течении в каналах некруглой формы
- •4.7. Ламинарное течение в зазорах
- •4.7.1. Течение через зазор между параллельными стенками под действием умеренного перепада давлений
- •4.7.2. Течение через зазор при больших перепадах давления
- •5. Турбулентное движение жидкости
- •5.1. Пульсация местной скорости в турбулентном потоке
- •5.2. Распределение осреднённых местных скоростей в турбулентном потоке
- •5.3. Гидравлически гладкие и шероховатые трубы
- •5.4. Потери по длине в гидравлически гладких трубах
- •5.6. Влияние шероховатости на потери. График Никурадзе
- •Заключение
- •Библиографический список
- •Оглавление
3.3. Линия тока и траектория частицы, элементарная струйка
Через
любую точку А
потока
(рис.3.3) всегда можно провести линию, в
каждой точке которой вектор местной
скорости в данный момент времени
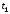 направлен по касательной к ней.
направлен по касательной к ней.
Линией тока называется линия, в каждой точке которой вектор скорости в данный момент времени направлен по касательной. Это понятие является центральным в методе Эйлера.

Рис. 3.3. Линия тока и траектория частицы жидкости
Траекторией
называется
путь, который описывает точка при своём
движении. При
установившемся движении
линия тока и траектория частицы совпадают.
В общем случае неустановившегося
движения в следующий момент времени
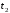 через ту же точку А может проходить уже
другая линия тока.
через ту же точку А может проходить уже
другая линия тока.
Вектор
скорости
 с компонентами
с компонентами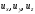 касателен к линии тока, т.е. совпадает
по направлению с элементами линии тока
касателен к линии тока, т.е. совпадает
по направлению с элементами линии тока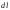 ,
имеющего проекции
,
имеющего проекции на оси координат. Воспользуемся известным
условием параллельности двух векторов
– их проекции на оси координат должны
быть пропорциональны друг другу
на оси координат. Воспользуемся известным
условием параллельности двух векторов
– их проекции на оси координат должны
быть пропорциональны друг другу
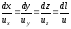 .
.
Полученное условие является уравнением линии тока в дифференциальной форме.
В частном случае при установившемся движении каждая линия тока сохраняет своё положение в пространстве и одновременно становится линией, по которой перемещаются частицы, т.е. совпадает с траекторией.
Элементарной
струйкой
называется совокупность линий тока,
проходящих через все точки бесконечно
малой площадки
 (рис.3.4).
(рис.3.4).

Рис.3.4. Элементарная струйка и трубка тока
При установившемся движении элементарная струйка сохраняет с течением времени постоянными свою форму, размеры и положение в пространстве, что является следствием аналогичного свойства составляющих её линий тока.
При стремлении поперечных размеров струйки к нулю она в пределе стягивается в линию тока.
Боковая поверхность элементарной струйки называется трубкой тока (рис.3.4). Трубка тока, таким образом, является как бы непроницаемой стенкой, а элементарная струйка представляет собой самостоятельный элементарный поток.
В случае установившегося движения элементарная струйка обладает следующими тремя свойствами:
1) Форма элементарной стройки не меняется во времени, т.к. при установившемся движении не меняется форма линий тока;
2) Поверхность элементарной струйки (трубки тока) непроницаема, т.е. перетекание через боковые стенки отсутствует. Частицы жидкости, движущиеся в одной линии тока, не могут принадлежать другим;
3) Скорость и давление для всех точек данного поперечного сечения струйки постоянны, однако вдоль струйки эти величины могут меняться.
Таким образом, при установившемся движении элементарная струйка сохраняет с течением времени постоянными свою форму, размеры и положение в пространстве. Массообмен через боковую поверхность исключён, и движение жидкости возможно только вдоль элементарной струйки.
Если
учесть несжимаемость жидкости, то
получим следствие,
лежащее в основе одного из центральных
положений гидравлики, – уравнение
неразрывности:
объём
жидкости, прошедший через любое поперечное
сечение с площадью
 за время
за время ,
должен равняться объёму жидкости,
прошедшему через любое другое сечение
с площадью
,
должен равняться объёму жидкости,
прошедшему через любое другое сечение
с площадью за то же время.
за то же время.
Невыполнение сформулированного условия привело бы к изменению массы жидкости между двумя сечениями, что противоречит свойствам принятой модели жидкости как несжимаемой среды.
