2.10.4. Равновесие жидкости в поле центробежных сил при нулевой или слабой гравитация

Пусть равномерно вращающийся сосуд принадлежит к системе, которая перемещается с некоторым ускорением, и пусть при этом инерционная сила переносного движения системы уравновешивает силу тяжести, (рис. 2.22).

Тогда независимо от направления оси вращения сосуда на содержащуюся в нем жидкость из всех массовых сип будет действовать только одна - центробежная. Действием силы тяжести можно пренебречь и в том случае, когда центробежное ускорение, вызываемое вращением сосуда, несоизмеримо больше ускорения свободного падения. В обоих случаях дифференциальные уравнения гидростатики упрощаются.

Так как движение симметрично относительно оси вращения, то рассмотрим равновесие частиц жидкости, расположенных в плоскости координат .

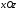Рис. 2.22. Равновесие жидкости

в равномерно вращающемся

сосуде при нулевой гравитации

Связав оси координат с сосудом и совместив ось с осью вращения (которая при отсутствии гравитации может иметь любое правление), используем основное дифференциальное уравнение гидростатики (2.10)

.

Подставляя значения проекции единичных массовых сил и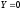,получим

.

Интегрируя, получаем закон распределения давления

.

Определим постоянную для граничных условий,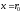

.

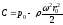Тогда

,

т.е. полное давление складывается из двух составляющих:

1) внешнего давления ;

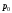2) давления от центробежной силы .

Дифференциальное уравнение поверхности (2.12) уровня примет вид

.

Уравнение будет равно нулю только в случае если , т.е..

Таким образом, как и следовало ожидать, поверхности равного давления представляют собой в нашем случае семейство соосных цилиндров с радиусами от 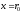до, где- внутренний радиус сосуда, а- радиус свободной поверхности (при полном заполнении сосуда жидкостью.

2.11. Формы поверхностей раздела между жидкостью и газом (паром) в условиях динамической невесомости

Динамическая невесомость характеризуется тем, что сила тяжести уравновешена инерционной силой переносного движения системы, т.е. результирующая массовых сил равна нулю. В этом случае отчетливо выраженной свободной поверхности может и не существовать, поскольку отсутствует массовая сила, действие которой и приводит к разделению жидкости и газа. В условиях невесомости весьма вероятно образование суспензии, т.е. смеси капельной жидкости и газа.

Отсутствие поля массовых сил приводит в условиях невесомости к увеличению роли сил поверхностного натяжения, которыми в гидромеханике обычно пренебрегают. В тех случаях, когда поверхность раздела между капельной жидкостью и газом в условиях невесомости существует, ее форма определяется действием сил поверхностного натяжения и зависит поэтому от краевого контактного угла 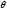, образуемого жидкостью со стенкой.

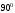В зависимости от величины этого угла капельные жидкости, как известно, могут быть разделены на смачивающие и не смачивающие стенку из того или иного материала. Если контактный угол меньше (рис. 2.23, 2.24, 2.25), то по отношению к данной стенке капельная жидкость принадлежит к смачивающим, если же этот угол превышает(рис. 2.26 и 2.27), жидкость следует рассматривать как не смачивающую.

а - при обычной гравитации; б - в условиях невесомости

Рис. 2.23. Смачивающая жидкость заполняет сферический

сосуд менее чем наполовину

а - обычная гравитация; б – невесомость

Рис. 2.24. Смачивающая жидкость заполняет сосуд

более чем наполовину

а - обычная гравитация; б – невесомость

Рис. 2.25. Полностью смачивающая жидкость ()

заполняет сферический сосуд менее чем наполовину

а - обычная гравитация; б – невесомость

Рис.2.26. Несмачивающая жидкость заполняет

сферический сосуд менее чем наполовину

а - обычная гравитация; б - невесомость.

Рис. 2.27. Несмачивающая жидкость заполняет

сферический сосуд почти полностью

При исследовании формы поверхности раздела между капельной жидкостью и газом (паром) необходимо исходить из того, что контактный угол, полностью определяемый действием адгезионных молекулярных сил, не зависит от наличия или отсутствия гравитации, и поэтому его величина в условиях невесомости будет такой же, как и в земных. (Силы молекулярного взаимодействия можно разделить на когезионные (между молекулами самой жидкости) и адгезионные (между молекулами жидкости и ограничивающего ее твердого тела или газа)).

Кроме того, следует учитывать, что форма поверхности раздела определяется не только углом контакта, но и такими факторами, как форма сосуда и степень заполнения его жидкостью.

На рис.2.23 - 2.27 приведены характерные формы поверхности раздела капельной жидкости и газа в сферических сосудах по З. Каллагану [3].

В заключение отметим, что при отсутствии поля массовых сил давление не зависит от глубины погружения рассматриваемой точки и в пределах любого непрерывного объема жидкости остается одинаковым.