
- •Г.И. Скоморохов
- •Введение
- •Основные физические свойства жидкостей
- •1.1. Определение жидкости
- •1.2. Классификация сил, действующих в жидкости
- •1.3. Основные физические свойства жидкостей
- •Гидростатика
- •2.1. Основные понятия гидростатики
- •2.1.2. Давление абсолютное, избыточное, вакуум
- •2.1.3. Свойства гидростатического давления
- •2.1.4. Основное уравнение гидростатики. Закон Паскаля
- •2.1.5. Поверхности уровня
- •2.2. Дифференциальные уравнения гидростатики
- •2.2.2. Основное дифференциальное уравнение гидростатики
- •2.2.3. Дифференциальное уравнение поверхности
- •2.3. Основные задачи гидростатики
- •2.4. Основное уравнение гидростатики из уравнений Эйлера. Закон распределения давления
- •2.4.1. Геометрическая интерпретация основного уравнения гидростатики
- •2.4.2. Энергетическая интерпретация основного уравнения гидростатики
- •2.5. Применение закона Паскаля в технике
- •2.5.1. Приборы для измерения давления
- •2.5.2. Простейшие гидравлические машины.
- •2.5.1. Приборы для измерения давления
- •2.5.2. Простейшие гидравлические машины. Гидравлический пресс. Мультипликатор
- •2.6. Сила давления на плоскую стенку. Гидравлический парадокс
- •2.7. Центр давления
- •2.8. Сила давления жидкости на криволинейные стенки
- •2.9. Закон Архимеда
- •2.10. Относительное равновесие жидкости
- •2.10.1. Движение сосуда с жидкостью прямолинейно в произвольном направлении с постоянным ускорением
- •2.10.2. Движение сосуда с жидкостью вертикально вниз с постоянным ускорением
- •2.10.3. Равномерное вращение цилиндрического сосуда с жидкостью вокруг вертикальной оси
- •2.10.4. Равновесие жидкости в поле центробежных сил при нулевой или слабой гравитация
- •2.11. Формы поверхностей раздела между жидкостью и газом (паром) в условиях динамической невесомости
- •3. Гидродинамика
- •3.2. Виды движения жидкости
- •3.3. Линия тока и траектория частицы, элементарная струйка
- •3.4. Закон сохранения массы. Расход. Уравнение неразрывности
- •3.5. Живое сечение. Смоченный периметр. Гидравлический радиус
- •3.6. Уравнение количества движения для потока жидкости
- •3.7. Дифференциальные уравнения движения идеальной жидкости в форме уравнений Эйлера
- •3.8. Основное дифференциальное уравнение установившегося движения идеальной жидкости
- •3.9. Уравнение Бернулли для струйки идеальной несжимаемой жидкости
- •3.9.1. Геометрический смысл уравнения Бернулли.
- •3.9.2. Энергетический смысл уравнения Бернулли
- •3.9.1. Геометрический смысл уравнения Бернулли. Трубка Пито
- •3.9.2. Энергетический смысл уравнения Бернулли
- •3.10. Уравнение Бернулли для элементарной струйки вязкой жидкости
- •3.11. Уравнение Бернулли для потока вязкой несжимаемой жидкости
- •3.12. Классификация гидравлических потерь. Гидравлический и пьезометрический уклоны
- •3.13. Применение уравнения Бернулли в технике
- •3.14. Основы гидродинамического подобия
- •3.15. Режимы течения жидкости
- •3.16. Критерий Рейнольдса и гидравлический радиус
- •4. Ламинарное течение жидкости
- •4.2. Расход при ламинарном режиме в круглой трубе. Формула Пуазейля. Коэффициент Кориолиса
- •4.3. Потери на трение. Формула Дарси-Вейсбаха
- •4.4. Влияние теплообмена на профиль скоростей и потери по длине
- •4.5. Начальный участок ламинарного потока
- •4.6. Потери на трение при ламинарном течении в каналах некруглой формы
- •4.7. Ламинарное течение в зазорах
- •4.7.1. Течение через зазор между параллельными стенками под действием умеренного перепада давлений
- •4.7.2. Течение через зазор при больших перепадах давления
- •5. Турбулентное движение жидкости
- •5.1. Пульсация местной скорости в турбулентном потоке
- •5.2. Распределение осреднённых местных скоростей в турбулентном потоке
- •5.3. Гидравлически гладкие и шероховатые трубы
- •5.4. Потери по длине в гидравлически гладких трубах
- •5.6. Влияние шероховатости на потери. График Никурадзе
- •Заключение
- •Библиографический список
- •Оглавление
2.10.1. Движение сосуда с жидкостью прямолинейно в произвольном направлении с постоянным ускорением
Пусть
сосуд с жидкостью движется прямолинейно
с постоянным ускорением
 в произвольном направлении, т.е.
равноускоренно или равнозамедленно
(рис. 2.19).
в произвольном направлении, т.е.
равноускоренно или равнозамедленно
(рис. 2.19).

Рис. 2.19. Силы, действующие при относительном покое
жидкости и прямолинейном равноускоренном движении
В
этом случае на любую точку
 в жидкости действуют две единичные
массовые силы:
в жидкости действуют две единичные
массовые силы: - сила тяжести;
- сила тяжести; - сила инерции переносного движения,
равная ускорению
- сила инерции переносного движения,
равная ускорению ,
но направленная в противоположную
сторону. Результирующая массовая сила
,
но направленная в противоположную
сторону. Результирующая массовая сила ,
действующая на жидкость, равна сумме
векторов силы тяжести и силы инерции,
и направлена нормально к свободной
поверхности. Проведя геометрическое
сложение этих единичных сил (ускорений),
получим результирующую единичную
массовую силу
,
действующая на жидкость, равна сумме
векторов силы тяжести и силы инерции,
и направлена нормально к свободной
поверхности. Проведя геометрическое
сложение этих единичных сил (ускорений),
получим результирующую единичную
массовую силу :
:
 ,
,
где
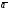 и
и - векторы единичных сил инерции и сил
тяжести.
- векторы единичных сил инерции и сил
тяжести.
Оси
координат жестко свяжем с сосудом. Для
упрощения вывода ось
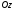 проведём параллельно результирующему
вектору
проведём параллельно результирующему
вектору ,
но направим в противоположную сторону.
Оси
,
но направим в противоположную сторону.
Оси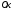 и
и расположим в плоскости, нормальной к
оси
расположим в плоскости, нормальной к
оси .
.
Поверхности
уровня в этом случае представляет собой
семейство плоскостей, нормальных к
вектору
 ,
т.е. параллельных плоскости
,
т.е. параллельных плоскости .
Одна из них совпадает со свободной
поверхностью жидкости (
.
Одна из них совпадает со свободной
поверхностью жидкости ( ;
; ).
).
Применим к этому случаю основное дифференциальное уравнение гидростатики (2.10)
 .
.
Для
нашего случая проекции единичных
массовых сил будут равны
 ,
, и
и .
.
Тогда уравнение гидростатики примет вид
 ,
,
или
 .
.
После интегрирования получаем
 .
.
Постоянную
интегрирования
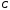 найдем из условий на свободной поверхности,
т.е. для
найдем из условий на свободной поверхности,
т.е. для ;
; :
:
 ,
,
или
 .
.
Но
 - глубина погружения точки
- глубина погружения точки относительно свободной поверхности
относительно свободной поверхности
 .
.
Таков закон распределения давления в рассматриваемом случае.
Учитывая,
что
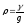 ,
а отношение
,
а отношение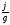 может быть названо коэффициентом
перегрузки,
то закон распределения давления можно
записать в другой форме:
может быть названо коэффициентом
перегрузки,
то закон распределения давления можно
записать в другой форме:
 ,
,
где
 -коэффициент
перегрузки.
-коэффициент
перегрузки.
При
давлении на свободной поверхности,
равном атмосферному
 ,
избыточное давление в точке
,
избыточное давление в точке определяется формулой
определяется формулой
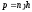 .
.
Для
определения угла наклона свободной
поверхности жидкости при произвольном
движении необходимо знать угол наклона
вектора ускорения
 относительно оси
относительно оси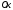 .
.
2.10.2. Движение сосуда с жидкостью вертикально вниз с постоянным ускорением
Предположим,
что открытый резервуар вместе с
находящейся в ней жидкостью движется
в вертикальном направлении сверху вниз
с некоторым постоянным ускорением
 ,
равным или меньшим ускорению свободного
падения
,
равным или меньшим ускорению свободного
падения (рис. 2.20).
(рис. 2.20).
В
этом случае на любую точку
 в жидкости действуют две единичные
массовые силы:
в жидкости действуют две единичные
массовые силы:
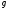 -
сила тяжести;
-
сила тяжести;
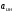 -
сила инерции переносного движения.
-
сила инерции переносного движения.
Результирующая
массовая сила
 ,
действующая на жидкость, равна сумме
векторов силы тяжести и силы инерции,
и направлена в сторону, обратную ускорению
,
действующая на жидкость, равна сумме
векторов силы тяжести и силы инерции,
и направлена в сторону, обратную ускорению .
.

Рис. 2.20. Относительное равновесие жидкости
при движении по вертикали
Обозначив
вектор равнодействующей массовой силы,
отнесенной к единице массы, через
 получим
получим
 ,
,
где
 и
и - векторы единичных сил инерции и
тяжести.
- векторы единичных сил инерции и
тяжести.
Определим:
1) вид поверхности уровня;
2) закон распределения гидростатического давления.
Заметим, что, согласно принципу Даламбера, при любом движении тела можно пользоваться уравнениями статики, если к системе действующих сил прибавить силы инерции (они направлены в сторону, противоположную направлению движения). Такая система сил будет уравновешена, и тело можно считать находящимся в равновесном состоянии. Воспользуемся дифференциальным уравнением поверхности уровня (2.12)
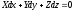 .
.
Определим
для данного случая проекции единичных
массовых сил
 ,
,
 и
и
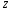 ,
которые численно равны ускорениям.
Ускорение свободного падения
,
которые численно равны ускорениям.
Ускорение свободного падения (9,81
м/с2)
и ускорение сил инерции
(9,81
м/с2)
и ускорение сил инерции
 направлены параллельно оси
направлены параллельно оси .
Следовательно,
проекции этих ускорений на оси
.
Следовательно,
проекции этих ускорений на оси
 и
и
 равны
нулю:
равны
нулю:
 и
и .
Проекция на ось
.
Проекция на ось равна
равна
 .
.
Подставив
 в дифференциальное уравнение поверхности,
получим
в дифференциальное уравнение поверхности,
получим
 .
.
Учитывая,
что
 ,
а
,
а ,
т.е.
,
т.е.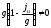 ,
следовательно, для выполнения равенства
необходимо, чтобы
,
следовательно, для выполнения равенства
необходимо, чтобы .
.
Интегрируя
последнее выражение, находим
 .
А это значит, чтоповерхность
уровня будет горизонтальной плоскостью.
.
А это значит, чтоповерхность
уровня будет горизонтальной плоскостью.
Если
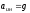 ,
то
,
то
 и
тогда
и
тогда
 может
быть и не равным нулю, следовательно,
форма
свободной поверхности может быть
произвольной.
может
быть и не равным нулю, следовательно,
форма
свободной поверхности может быть
произвольной.
Определим теперь закон распределения гидростатического давления для этого случая. Запишем основное уравнение гидростатики в дифференциальной форме (2.10)
 .
.
Для
нашего случая ось
 направлена вертикально вверх, а оси
направлена вертикально вверх, а оси и
и лежат в плоскости нормальной оси
лежат в плоскости нормальной оси ,
поэтому проекции единичных массовых
сил будут равны
,
поэтому проекции единичных массовых
сил будут равны и
и и
и .
.
Тогда уравнение гидростатики примет вид
 .
.
Так
как
 ,
получим
,
получим
 ,
,
Введем обозначение
 .
.
где
 представляет собой объемный вес жидкости
представляет собой объемный вес жидкости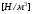 в условиях вертикального спуска с
ускорением
в условиях вертикального спуска с
ускорением ;
;
 -
коэффициент перегрузки или просто
перегрузка.
-
коэффициент перегрузки или просто
перегрузка.
Делая подстановку, получим
 ,
,
и после интегрирования найдем закон распределения давления
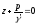 . (2.27)
. (2.27)
Таким
образом, в условиях спуска по вертикали
с ускорением
 закон распределения гидростатического
давления будет таким же, как и в обычных
условиях равновесия жидкости в поле
земного тяготения. Отличие заключается
в том, что в подвижной системе координат
удельный вес жидкости зависит от
коэффициента перегрузки
закон распределения гидростатического
давления будет таким же, как и в обычных
условиях равновесия жидкости в поле
земного тяготения. Отличие заключается
в том, что в подвижной системе координат
удельный вес жидкости зависит от
коэффициента перегрузки .
.
Причем,
если
 ,
то
при свободном падении, объемный вес
,
то
при свободном падении, объемный вес
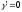 ,
т.е. жидкость стала«невесомой».
,
т.е. жидкость стала«невесомой».
Если
ускорение
 имеет знак минус,
т.е.
происходит торможение, объемный вес
имеет знак минус,
т.е.
происходит торможение, объемный вес
 будет
«тяжелее»
в
будет
«тяжелее»
в
 раз. Таким образом, вес жидкости при
относительном равновесии зависит от
коэффициента перегрузки.
раз. Таким образом, вес жидкости при
относительном равновесии зависит от
коэффициента перегрузки.
