
- •Г.И. Скоморохов
- •Введение
- •Основные физические свойства жидкостей
- •1.1. Определение жидкости
- •1.2. Классификация сил, действующих в жидкости
- •1.3. Основные физические свойства жидкостей
- •Гидростатика
- •2.1. Основные понятия гидростатики
- •2.1.2. Давление абсолютное, избыточное, вакуум
- •2.1.3. Свойства гидростатического давления
- •2.1.4. Основное уравнение гидростатики. Закон Паскаля
- •2.1.5. Поверхности уровня
- •2.2. Дифференциальные уравнения гидростатики
- •2.2.2. Основное дифференциальное уравнение гидростатики
- •2.2.3. Дифференциальное уравнение поверхности
- •2.3. Основные задачи гидростатики
- •2.4. Основное уравнение гидростатики из уравнений Эйлера. Закон распределения давления
- •2.4.1. Геометрическая интерпретация основного уравнения гидростатики
- •2.4.2. Энергетическая интерпретация основного уравнения гидростатики
- •2.5. Применение закона Паскаля в технике
- •2.5.1. Приборы для измерения давления
- •2.5.2. Простейшие гидравлические машины.
- •2.5.1. Приборы для измерения давления
- •2.5.2. Простейшие гидравлические машины. Гидравлический пресс. Мультипликатор
- •2.6. Сила давления на плоскую стенку. Гидравлический парадокс
- •2.7. Центр давления
- •2.8. Сила давления жидкости на криволинейные стенки
- •2.9. Закон Архимеда
- •2.10. Относительное равновесие жидкости
- •2.10.1. Движение сосуда с жидкостью прямолинейно в произвольном направлении с постоянным ускорением
- •2.10.2. Движение сосуда с жидкостью вертикально вниз с постоянным ускорением
- •2.10.3. Равномерное вращение цилиндрического сосуда с жидкостью вокруг вертикальной оси
- •2.10.4. Равновесие жидкости в поле центробежных сил при нулевой или слабой гравитация
- •2.11. Формы поверхностей раздела между жидкостью и газом (паром) в условиях динамической невесомости
- •3. Гидродинамика
- •3.2. Виды движения жидкости
- •3.3. Линия тока и траектория частицы, элементарная струйка
- •3.4. Закон сохранения массы. Расход. Уравнение неразрывности
- •3.5. Живое сечение. Смоченный периметр. Гидравлический радиус
- •3.6. Уравнение количества движения для потока жидкости
- •3.7. Дифференциальные уравнения движения идеальной жидкости в форме уравнений Эйлера
- •3.8. Основное дифференциальное уравнение установившегося движения идеальной жидкости
- •3.9. Уравнение Бернулли для струйки идеальной несжимаемой жидкости
- •3.9.1. Геометрический смысл уравнения Бернулли.
- •3.9.2. Энергетический смысл уравнения Бернулли
- •3.9.1. Геометрический смысл уравнения Бернулли. Трубка Пито
- •3.9.2. Энергетический смысл уравнения Бернулли
- •3.10. Уравнение Бернулли для элементарной струйки вязкой жидкости
- •3.11. Уравнение Бернулли для потока вязкой несжимаемой жидкости
- •3.12. Классификация гидравлических потерь. Гидравлический и пьезометрический уклоны
- •3.13. Применение уравнения Бернулли в технике
- •3.14. Основы гидродинамического подобия
- •3.15. Режимы течения жидкости
- •3.16. Критерий Рейнольдса и гидравлический радиус
- •4. Ламинарное течение жидкости
- •4.2. Расход при ламинарном режиме в круглой трубе. Формула Пуазейля. Коэффициент Кориолиса
- •4.3. Потери на трение. Формула Дарси-Вейсбаха
- •4.4. Влияние теплообмена на профиль скоростей и потери по длине
- •4.5. Начальный участок ламинарного потока
- •4.6. Потери на трение при ламинарном течении в каналах некруглой формы
- •4.7. Ламинарное течение в зазорах
- •4.7.1. Течение через зазор между параллельными стенками под действием умеренного перепада давлений
- •4.7.2. Течение через зазор при больших перепадах давления
- •5. Турбулентное движение жидкости
- •5.1. Пульсация местной скорости в турбулентном потоке
- •5.2. Распределение осреднённых местных скоростей в турбулентном потоке
- •5.3. Гидравлически гладкие и шероховатые трубы
- •5.4. Потери по длине в гидравлически гладких трубах
- •5.6. Влияние шероховатости на потери. График Никурадзе
- •Заключение
- •Библиографический список
- •Оглавление
2.9. Закон Архимеда
Описанный
выше прием нахождения вертикальной
составляющей силы давления жидкости
на криволинейную стенку используют для
доказательства закона Архимеда. Пусть
в жидкость погружено тело произвольной
формы объемом
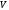 (рис.
2.18).
(рис.
2.18).
Спроектируем
его сечение на свободную поверхность
жидкости и проведем проектирующую
цилиндрическую поверхность, которая
касается поверхности тела по замкнутой
кривой. Эта кривая отделяет верхнюю
часть поверхности тела
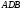 от
нижней ее части
от
нижней ее части
 .
.
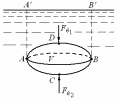
Рис. 2.18. Схема для доказательства закона Архимеда
Вертикальная
составляющая
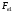 силы
избыточного давления жидкости на верхнюю
часть поверхности тела направлена вниз
и равна весу жидкости в объеме
силы
избыточного давления жидкости на верхнюю
часть поверхности тела направлена вниз
и равна весу жидкости в объеме
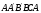
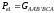 .
.
Вертикальная
составляющая
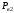 силы
давления жидкости на нижнюю часть
поверхности тела направлена вверх и
равна весу жидкости в объеме
силы
давления жидкости на нижнюю часть
поверхности тела направлена вверх и
равна весу жидкости в объеме
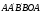
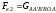 .
.
Отсюда следует, что вертикальная равнодействующая сил давления жидкости на тело будет направлена вверх и равна весу жидкости в объеме, равном разности указанных двух объемов, т.е.
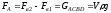 .
.
В этом и заключается закон Архимеда, обычно формулируемый так: на тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх, численно равная весу жидкости, вытесненной телом, и приложенная в центре тяжести объема погруженной части тела.
Сила
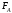 .
называется
архимедовой
силой,
или
силой
поддержания,
а
точка ее приложения, т.е. центр тяжести
объема
.
называется
архимедовой
силой,
или
силой
поддержания,
а
точка ее приложения, т.е. центр тяжести
объема
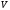 -
центром
водоизмещения.
-
центром
водоизмещения.
В
зависимости от соотношения веса
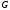 тела
и архимедовой силы
тела
и архимедовой силы
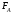 возможны
три случая:
возможны
три случая:
1)
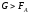 - тело
тонет;
- тело
тонет;
2)
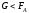 -
теловсплывает
и плавает
на поверхности жидкости в частично
погруженном состоянии;
-
теловсплывает
и плавает
на поверхности жидкости в частично
погруженном состоянии;
3)
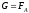 -
тело плавает
в полностью погруженном состоянии.
-
тело плавает
в полностью погруженном состоянии.
Для
равновесия плавающего тела кроме
равенства сил
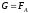 должен быть равен нулю суммарный момент.
Последнее условие соблюдается тогда,
когда центр тяжести тела лежит на одной
вертикали с центром водоизмещения.
должен быть равен нулю суммарный момент.
Последнее условие соблюдается тогда,
когда центр тяжести тела лежит на одной
вертикали с центром водоизмещения.
Условие устойчивого равновесия тела, плавающего в полностью погруженном состоянии, заключается в следующем: центр тяжести тела должен находиться ниже центра водоизмещения. Устойчивость равновесия тел, плавающих на поверхности жидкости, здесь не рассматривается.
2.10. Относительное равновесие жидкости
в движущихся сосудах

2.10.1. Движение сосуда с жидкостью прямолинейно в
произвольном направлении с постоянным ускорением
2.10.2. Движение сосуда с жидкостью вертикально вниз
с постоянным ускорением
2.10.3. Равномерное вращение цилиндрического сосуда
с жидкостью вокруг вертикальной оси
2.10.4. Равновесие жидкости в поле центробежных сил
при нулевой или слабой гравитация

Ранее было рассмотрено равновесие жидкости под действием лишь одной массовой силы - ее веса. Этот случай имеет место тогда, когда жидкость покоится в сосуде, неподвижном относительно Земли. При этом свободная и прочие поверхности уровня жидкости представляют собой горизонтальные плоскости.
Относительным равновесием жидкости называется такой случай ее движения, при котором вся масса жидкости движется как твердое тело, а отдельные ее частицы не смещаются одна относительно другой. Например, представим, что некоторый замкнутый сосуд с жидкостью движется с постоянной скоростью (или постоянным ускорением) в любом направлении, тогда с этой же скоростью (или ускорением) движется также и каждая частица жидкости. Очевидно, что рассматриваемая масса жидкости будет неподвижна в координатной системе, связанной с движущимся резервуаром. Такое движение жидкости представляет собой относительное ее равновесие.
При относительном покое свободная поверхность жидкости и прочие поверхности уровня могут существенно отличаться от поверхностей уровня при покое жидкости в неподвижном сосуде, т.е. от горизонтальной плоскости. При определении формы и положения свободной поверхности жидкости, находящейся в относительном покое, следует руководствоваться основным свойством всякой поверхности уровня, которое заключается в следующем: равнодействующая массовых сил всегда действует нормально к поверхности уровня. В самом деле, если бы равнодействующая массовая сила действовала под некоторым углом к поверхности уровня, то касательная составляющая этой силы вызывала бы перемещение частиц жидкости вдоль поверхности уровня.
Рассмотрим три практически наиболее интересных случая относительного покоя жидкости:1) движение сосуда прямолинейно в произвольном направлении; 2) движение сосуда по вертикали; и 3) вращательное движение относительно вертикальной оси.
