2.7. Центр давления

При решении технических задач необходимо знать не только величину и направление силы давления, но во многих случаях и величину момента этой силы относительно той или иной оси.

Определение же момента невозможно без учета координат точки приложения результирующей силы, так называемого центра давления, т.е. точки пересечения вектора силы со смоченной поверхностью стенки. В общем случае центр давления расположен глубже центра тяжести смоченной площади. Это объясняется тем, что давление распределяется неравномерно по высоте: чем глубже точка от поверхности, тем больше давление в этой точке.

Определим координаты центра давления 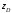при условии, что давление на свободной поверхности равно атмосферному, следовательно, избыточное давлении распределяется по закону треугольника (рис. 2.15). (При рассмотрении свойств жидкости, указывалось, что в жидкостях возможны лишь распределенные силы, поэтому центры давления можно рассматривать лишь условно?)

Так как внешнее давление 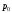передается всем точкам площади 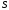одинаково, то его равнодействующая сила 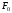будет приложена в центре тяжести площади 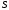. Для определения ординаты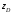центра избыточного давления приравняем момент результирующей силы избыточного давления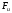относительно оси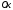сумме моментов сил, действующих на элементарные площадки, относительно той же оси

,

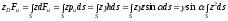(2.24)

где .

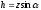Учитывая, что

,

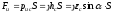а интеграл 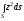есть не что иное, как момент инерции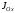площади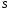относительно оси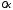(от которой отмечается ордината), подставим их значения в (2.24) и решим относительно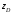. Откуда

.

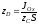От момента инерции 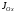можно перейти к моменту инерции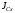площад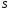иотносительно оси, проходящей через центр тяжести этой площади параллельно оси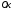

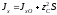, (2.25)

где 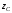- ордината центра тяжести площади.

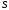Подставляя значение 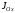из формулы (2.25) в формулу (2.24), получим

,

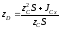т.е.

. (2.26)

Таким образом, центр давления расположен глубже центра тяжести смоченной площади стенки. Смещение центра давления относительно центра тяжести иногда называют эксцентриситетом давления

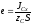. (2.27)

В виде примера определим силу избыточного давления на вертикальную прямоугольную стенку 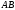(рис. 2.16).

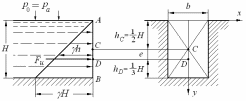
Рис.2.16

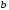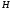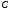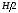Пусть ширина стенки;- высота уровня жидкости перед стенкой. Будем считать, что по другую сторону стенки, как и на свободной поверхности жидкости, давление равно атмосферному. Центр тяжестилежит на пересечении диагоналей прямоугольника, т.е. на глубине. Избыточное давление на этой глубине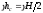. Сила давления на стенку равна произведению давления в точке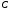на площадь прямоугольника:

.

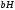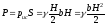_{Определим глубину погружения центра избыточного да}вления по формуле (2.26), учитывая, что момент инерции прямоугольника :

.

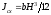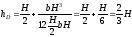Как исследовало ожидать, центр давления лежит на той же глубине, что и центр тяжести эпюры давления, которая в данном случае представляет собой прямоугольный треугольник.

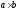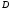Таким образом, в частном случае, когда стенка имеет форму прямоугольника размерами (рис. 2.16) и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления находится на расстоянии 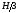от нижней стороны.